def layer_forward(x, w):
  """ Receive inputs x and weights w """
  # Do some computations ...
  z = # ... some intermediate value
  # Do some more computations ...
  out = # the output
   
  cache = (x, w, z, out) # Values we need to compute gradients
   
  return out, cache

def layer_backward(dout, cache):
  """
  Receive dout (derivative of loss with respect to outputs) and cache,
  and compute derivative with respect to inputs.
  """
  # Unpack cache values
  x, w, z, out = cache
  
  # Use values in cache to compute derivatives
  dx = # Derivative of loss with respect to x
  dw = # Derivative of loss with respect to w
  
  return dx, dw

# As usual, a bit of setup
from __future__ import print_function
import time
import numpy as np
import matplotlib.pyplot as plt
from cs231n.classifiers.fc_net import *
from cs231n.data_utils import get_CIFAR10_data
from cs231n.gradient_check import eval_numerical_gradient, eval_numerical_gradient_array
from cs231n.solver import Solver

%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2

def rel_error(x, y):
  """ returns relative error """
  return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))

# Load the (preprocessed) CIFAR10 data.

data = get_CIFAR10_data()
for k, v in list(data.items()):
  print(('%s: ' % k, v.shape))

# Test the affine_forward function

num_inputs = 2
input_shape = (4, 5, 6)
output_dim = 3

input_size = num_inputs * np.prod(input_shape)
weight_size = output_dim * np.prod(input_shape)

x = np.linspace(-0.1, 0.5, num=input_size).reshape(num_inputs, *input_shape)
w = np.linspace(-0.2, 0.3, num=weight_size).reshape(np.prod(input_shape), output_dim)
b = np.linspace(-0.3, 0.1, num=output_dim)

out, _ = affine_forward(x, w, b)
correct_out = np.array([[ 1.49834967,  1.70660132,  1.91485297],
                        [ 3.25553199,  3.5141327,   3.77273342]])

# Compare your output with ours. The error should be around e-9 or less.
print('Testing affine_forward function:')
print('difference: ', rel_error(out, correct_out))

# Test the affine_backward function
np.random.seed(231)
x = np.random.randn(10, 2, 3)
w = np.random.randn(6, 5)
b = np.random.randn(5)
dout = np.random.randn(10, 5)

dx_num = eval_numerical_gradient_array(lambda x: affine_forward(x, w, b)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: affine_forward(x, w, b)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: affine_forward(x, w, b)[0], b, dout)

_, cache = affine_forward(x, w, b)
dx, dw, db = affine_backward(dout, cache)

# The error should be around e-10 or less
print('Testing affine_backward function:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))

# Test the relu_forward function

x = np.linspace(-0.5, 0.5, num=12).reshape(3, 4)

out, _ = relu_forward(x)
correct_out = np.array([[ 0.,          0.,          0.,          0.,        ],
                        [ 0.,          0.,          0.04545455,  0.13636364,],
                        [ 0.22727273,  0.31818182,  0.40909091,  0.5,       ]])

# Compare your output with ours. The error should be on the order of e-8
print('Testing relu_forward function:')
print('difference: ', rel_error(out, correct_out))

np.random.seed(231)
x = np.random.randn(10, 10)
dout = np.random.randn(*x.shape)

dx_num = eval_numerical_gradient_array(lambda x: relu_forward(x)[0], x, dout)

_, cache = relu_forward(x)
dx = relu_backward(dout, cache)

# The error should be on the order of e-12
print('Testing relu_backward function:')
print('dx error: ', rel_error(dx_num, dx))

from cs231n.layer_utils import affine_relu_forward, affine_relu_backward
np.random.seed(231)
x = np.random.randn(2, 3, 4)
w = np.random.randn(12, 10)
b = np.random.randn(10)
dout = np.random.randn(2, 10)

out, cache = affine_relu_forward(x, w, b)
dx, dw, db = affine_relu_backward(dout, cache)

dx_num = eval_numerical_gradient_array(lambda x: affine_relu_forward(x, w, b)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: affine_relu_forward(x, w, b)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: affine_relu_forward(x, w, b)[0], b, dout)

# Relative error should be around e-10 or less
print('Testing affine_relu_forward and affine_relu_backward:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))

np.random.seed(231)
num_classes, num_inputs = 10, 50
x = 0.001 * np.random.randn(num_inputs, num_classes)
y = np.random.randint(num_classes, size=num_inputs)

dx_num = eval_numerical_gradient(lambda x: svm_loss(x, y)[0], x, verbose=False)
loss, dx = svm_loss(x, y)

# Test svm_loss function. Loss should be around 9 and dx error should be around the order of e-9
print('Testing svm_loss:')
print('loss: ', loss)
print('dx error: ', rel_error(dx_num, dx))

dx_num = eval_numerical_gradient(lambda x: softmax_loss(x, y)[0], x, verbose=False)
loss, dx = softmax_loss(x, y)

# Test softmax_loss function. Loss should be close to 2.3 and dx error should be around e-8
print('\nTesting softmax_loss:')
print('loss: ', loss)
print('dx error: ', rel_error(dx_num, dx))

np.random.seed(231)
N, D, H, C = 3, 5, 50, 7
X = np.random.randn(N, D)
y = np.random.randint(C, size=N)

std = 1e-3
model = TwoLayerNet(input_dim=D, hidden_dim=H, num_classes=C, weight_scale=std)

print('Testing initialization ... ')
W1_std = abs(model.params['W1'].std() - std)
b1 = model.params['b1']
W2_std = abs(model.params['W2'].std() - std)
b2 = model.params['b2']
assert W1_std < std / 10, 'First layer weights do not seem right'
assert np.all(b1 == 0), 'First layer biases do not seem right'
assert W2_std < std / 10, 'Second layer weights do not seem right'
assert np.all(b2 == 0), 'Second layer biases do not seem right'

print('Testing test-time forward pass ... ')
model.params['W1'] = np.linspace(-0.7, 0.3, num=D*H).reshape(D, H)
model.params['b1'] = np.linspace(-0.1, 0.9, num=H)
model.params['W2'] = np.linspace(-0.3, 0.4, num=H*C).reshape(H, C)
model.params['b2'] = np.linspace(-0.9, 0.1, num=C)
X = np.linspace(-5.5, 4.5, num=N*D).reshape(D, N).T
scores = model.loss(X)
correct_scores = np.asarray(
  [[11.53165108,  12.2917344,   13.05181771,  13.81190102,  14.57198434, 15.33206765,  16.09215096],
   [12.05769098,  12.74614105,  13.43459113,  14.1230412,   14.81149128, 15.49994135,  16.18839143],
   [12.58373087,  13.20054771,  13.81736455,  14.43418138,  15.05099822, 15.66781506,  16.2846319 ]])
scores_diff = np.abs(scores - correct_scores).sum()
assert scores_diff < 1e-6, 'Problem with test-time forward pass'

print('Testing training loss (no regularization)')
y = np.asarray([0, 5, 1])
loss, grads = model.loss(X, y)
correct_loss = 3.4702243556
assert abs(loss - correct_loss) < 1e-10, 'Problem with training-time loss'

model.reg = 1.0
loss, grads = model.loss(X, y)
correct_loss = 26.5948426952
assert abs(loss - correct_loss) < 1e-10, 'Problem with regularization loss'

# Errors should be around e-7 or less
for reg in [0.0, 0.7]:
  print('Running numeric gradient check with reg = ', reg)
  model.reg = reg
  loss, grads = model.loss(X, y)

  for name in sorted(grads):
    f = lambda _: model.loss(X, y)[0]
    grad_num = eval_numerical_gradient(f, model.params[name], verbose=False)
    print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))

input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
model = TwoLayerNet(input_size, hidden_size, num_classes)
solver = None

##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves about 36% #
# accuracy on the validation set.                                            #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

solver = Solver(model, data,
                update_rule='sgd', optim_config={'learning_rate':1e-3},
                lr_decay = 0.95, num_epochs = 10, batch_size = 200,
                print_every=100)
solver.train()

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
#                             END OF YOUR CODE                               #
##############################################################################

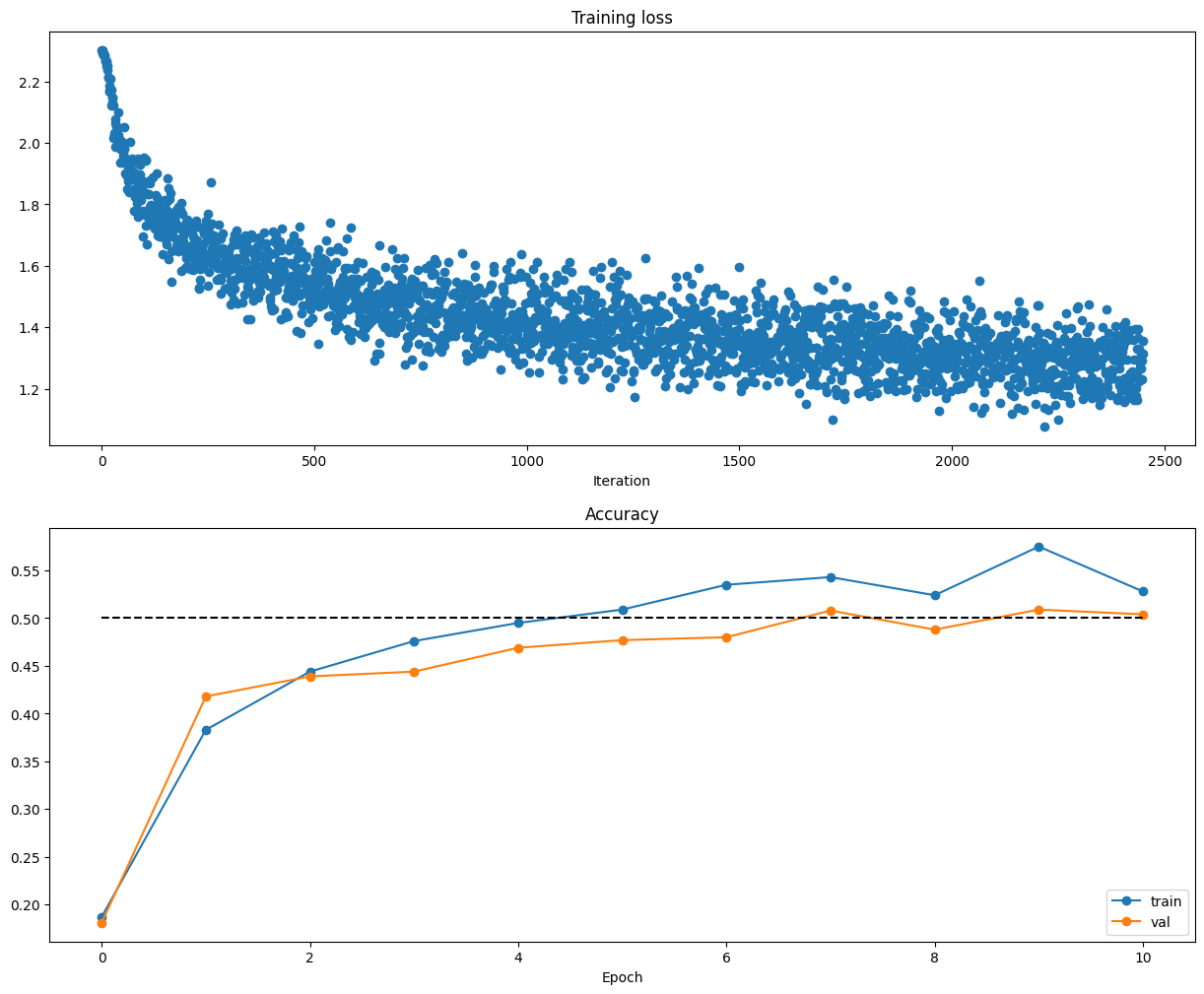
# Run this cell to visualize training loss and train / val accuracy

plt.subplot(2, 1, 1)
plt.title('Training loss')
plt.plot(solver.loss_history, 'o')
plt.xlabel('Iteration')

plt.subplot(2, 1, 2)
plt.title('Accuracy')
plt.plot(solver.train_acc_history, '-o', label='train')
plt.plot(solver.val_acc_history, '-o', label='val')
plt.plot([0.5] * len(solver.val_acc_history), 'k--')
plt.xlabel('Epoch')
plt.legend(loc='lower right')
plt.gcf().set_size_inches(15, 12)
plt.show()

from cs231n.vis_utils import visualize_grid

# Visualize the weights of the network

def show_net_weights(net):
    W1 = net.params['W1']
    W1 = W1.reshape(3, 32, 32, -1).transpose(3, 1, 2, 0)
    plt.imshow(visualize_grid(W1, padding=3).astype('uint8'))
    plt.gca().axis('off')
    plt.show()

show_net_weights(model)

best_model = None


#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained  #
# model in best_model.                                                          #
#                                                                               #
# To help debug your network, it may help to use visualizations similar to the  #
# ones we used above; these visualizations will have significant qualitative    #
# differences from the ones we saw above for the poorly tuned network.          #
#                                                                               #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
# write code to sweep through possible combinations of hyperparameters          #
# automatically like we did on thexs previous exercises.                          #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
import itertools

results = {}
best_val = -1

learning_rates = [4e-4, 4e-2, 4]
regularization_str = [1e-6,1e-3,3]

for lr, reg in itertools.product(learning_rates, regularization_str):
  model = TwoLayerNet(hidden_dim=128, reg = reg)
  solver = Solver(model, data, optim_config={'learning_rate':lr}, num_epochs = 15, verbose= False)
  solver.train()

  results[(lr,reg)] = solver.best_val_acc

  if results[(lr,reg)] > best_val:
    best_val = results[(lr,reg)]
    best_model = model

for lr, reg in sorted(results):
  val_accuracy = results[(lr,reg)]
  print(f'lr : {lr}, reg : {reg}, accuracy : {val_accuracy}')

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
#                              END OF YOUR CODE                                #
################################################################################

y_val_pred = np.argmax(best_model.loss(data['X_val']), axis=1)
print('Validation set accuracy: ', (y_val_pred == data['y_val']).mean())

y_test_pred = np.argmax(best_model.loss(data['X_test']), axis=1)
print('Test set accuracy: ', (y_test_pred == data['y_test']).mean())