[CS231n]Exercise1.1 - kNN
Before begin…
CS231n exercise1.1 : kNN에 대한 본인의 풀이이다. 자세한 코드는 github에서 확인 가능하다.
k-Nearest Neighbor (kNN) exercise
Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the assignments page on the course website.
The kNN classifier consists of two stages:
- During training, the classifier takes the training data and simply remembers it
- During testing, kNN classifies every test image by comparing to all training images and transfering the labels of the k most similar training examples
- The value of k is cross-validated
In this exercise you will implement these steps and understand the basic Image Classification pipeline, cross-validation, and gain proficiency in writing efficient, vectorized code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Run some setup code for this notebook.
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
try:
del X_train, y_train
del X_test, y_test
print('Clear previously loaded data.')
except:
pass
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
1
2
3
4
Training data shape: (50000, 32, 32, 3)
Training labels shape: (50000,)
Test data shape: (10000, 32, 32, 3)
Test labels shape: (10000,)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Subsample the data for more efficient code execution in this exercise
num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)
1
(5000, 3072) (500, 3072)
1
2
3
4
5
6
7
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
We would now like to classify the test data with the kNN classifier. Recall that we can break down this process into two steps:
- First we must compute the distances between all test examples and all train examples.
- Given these distances, for each test example we find the k nearest examples and have them vote for the label
Lets begin with computing the distance matrix between all training and test examples. For example, if there are Ntr training examples and Nte test examples, this stage should result in a Nte x Ntr matrix where each element (i,j) is the distance between the i-th test and j-th train example.
Note: For the three distance computations that we require you to implement in this notebook, you may not use the np.linalg.norm() function that numpy provides.
First, open cs231n/classifiers/k_nearest_neighbor.py and implement the function compute_distances_two_loops that uses a (very inefficient) double loop over all pairs of (test, train) examples and computes the distance matrix one element at a time.
1
2
3
4
5
6
# Open cs231n/classifiers/k_nearest_neighbor.py and implement
# compute_distances_two_loops.
# Test your implementation:
dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)
1
(500, 5000)
1
2
3
4
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()

Inline Question 1
Notice the structured patterns in the distance matrix, where some rows or columns are visibly brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)
- What in the data is the cause behind the distinctly bright rows?
- What causes the columns?
$\color{blue}{\textit Your Answer:}$ 특정 행이 유독 밝은 이유는 해당 test이미지가 대부분의 train 이미지에 대해 낮은 유사성질(특성)을 가지기 때문이다. 더불어 특정 열이 유독 밝은 이유는 해당 train 이미지가 대부분의 test이미지에 대해 낮은 유사성질을 가진다고 볼 수 있다.
1
2
3
4
5
6
7
8
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
1
Got 137 / 500 correct => accuracy: 0.274000
You should expect to see approximately 27% accuracy. Now lets try out a larger k, say k = 5:
1
2
3
4
y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
1
Got 139 / 500 correct => accuracy: 0.278000
You should expect to see a slightly better performance than with k = 1.
Inline Question 2
We can also use other distance metrics such as L1 distance. For pixel values $p_{ij}^{(k)}$ at location $(i,j)$ of some image $I_k$,
the mean $\mu$ across all pixels over all images is \(\mu=\frac{1}{nhw}\sum_{k=1}^n\sum_{i=1}^{h}\sum_{j=1}^{w}p_{ij}^{(k)}\) And the pixel-wise mean $\mu_{ij}$ across all images is \(\mu_{ij}=\frac{1}{n}\sum_{k=1}^np_{ij}^{(k)}.\) The general standard deviation $\sigma$ and pixel-wise standard deviation $\sigma_{ij}$ is defined similarly.
Which of the following preprocessing steps will not change the performance of a Nearest Neighbor classifier that uses L1 distance? Select all that apply. To clarify, both training and test examples are preprocessed in the same way.
- Subtracting the mean $\mu$ ($\tilde{p}{ij}^{(k)}=p{ij}^{(k)}-\mu$.)
- Subtracting the per pixel mean $\mu_{ij}$ ($\tilde{p}{ij}^{(k)}=p{ij}^{(k)}-\mu_{ij}$.)
- Subtracting the mean $\mu$ and dividing by the standard deviation $\sigma$.
- Subtracting the pixel-wise mean $\mu_{ij}$ and dividing by the pixel-wise standard deviation $\sigma_{ij}$.
- Rotating the coordinate axes of the data, which means rotating all the images by the same angle. Empty regions in the image caused by rotation are padded with a same pixel value and no interpolation is performed.
$\color{blue}{\textit Your Answer:}$ 1
$\color{blue}{\textit Your Explanation:}$
L1 = $\sum_i\lvert x_i - y_i \rvert$
- 상수만큼 이동 : 거리 변하지 않음
- Pixel-wise shift : 상대적 위치가 변하면 거리도 달라짐
- Scaling(divide by deviation) : 거리 변함
- Rotating : 거리에 민감함으로 거리 변함
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Now lets speed up distance matrix computation by using partial vectorization
# with one loop. Implement the function compute_distances_one_loop and run the
# code below:
dists_one = classifier.compute_distances_one_loop(X_test)
# To ensure that our vectorized implementation is correct, we make sure that it
# agrees with the naive implementation. There are many ways to decide whether
# two matrices are similar; one of the simplest is the Frobenius norm. In case
# you haven't seen it before, the Frobenius norm of two matrices is the square
# root of the squared sum of differences of all elements; in other words, reshape
# the matrices into vectors and compute the Euclidean distance between them.
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('One loop difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')
1
2
One loop difference was: 0.000000
Good! The distance matrices are the same
Frobenius norm
\(\sqrt{\sum_i=1^D(x^{(test)}_i-x^{(train)}_i)^2}\)
1
2
3
4
5
6
7
8
9
10
11
# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')
1
2
No loop difference was: 0.000000
Good! The distance matrices are the same
How to formulate the l2 distance using~
- 내적 계산 : $ X \cdot X^\top_{\text{train}} $
- 제곱합 벡터 만들기
- 브로드캐스팅 합 + 곱으로 거리 제곱 행렬 구성
- 제곱근 취해서 l2거리 완성
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Let's compare how fast the implementations are
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
# You should see significantly faster performance with the fully vectorized implementation!
# NOTE: depending on what machine you're using,
# you might not see a speedup when you go from two loops to one loop,
# and might even see a slow-down.
1
2
3
Two loop version took 41.406305 seconds
One loop version took 49.704700 seconds
No loop version took 1.123706 seconds
Cross-validation
We have implemented the k-Nearest Neighbor classifier but we set the value k = 5 arbitrarily. We will now determine the best value of this hyperparameter with cross-validation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# dists_two = classifier.compute_distances_no_loops(X_test)
# num_correct = np.sum(y_test_pred == y_test)
# accuracy = float(num_correct) / num_test
# for i in range(num_folds):
# classifier.train(X_train_folds[i], y_train_folds[i])
# dists = classifier.compute_distances_no_loops(X_test)
# for k in k_choices:
# prediction = classifier.predict_labels(dists, k=k)
for k in k_choices:
k_to_accuracies[k] = []
for i in range(num_folds):
X_val = X_train_folds[i]
y_val = y_train_folds[i]
X_train_cv = np.concatenate(X_train_folds[:i] + X_train_folds[i+1:], axis=0)
y_train_cv = np.concatenate(y_train_folds[:i] + y_train_folds[i+1:], axis=0)
classifier.train(X_train_cv, y_train_cv)
y_pred = classifier.predict(X_val, k=k)
accuracy = np.mean(y_pred == y_val)
k_to_accuracies[k].append(accuracy)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
k = 1, accuracy = 0.263000
k = 1, accuracy = 0.257000
k = 1, accuracy = 0.264000
k = 1, accuracy = 0.278000
k = 1, accuracy = 0.266000
k = 3, accuracy = 0.239000
k = 3, accuracy = 0.249000
k = 3, accuracy = 0.240000
k = 3, accuracy = 0.266000
k = 3, accuracy = 0.254000
k = 5, accuracy = 0.248000
k = 5, accuracy = 0.266000
k = 5, accuracy = 0.280000
k = 5, accuracy = 0.292000
k = 5, accuracy = 0.280000
k = 8, accuracy = 0.262000
k = 8, accuracy = 0.282000
k = 8, accuracy = 0.273000
k = 8, accuracy = 0.290000
k = 8, accuracy = 0.273000
k = 10, accuracy = 0.265000
k = 10, accuracy = 0.296000
k = 10, accuracy = 0.276000
k = 10, accuracy = 0.284000
k = 10, accuracy = 0.280000
k = 12, accuracy = 0.260000
k = 12, accuracy = 0.295000
k = 12, accuracy = 0.279000
k = 12, accuracy = 0.283000
k = 12, accuracy = 0.280000
k = 15, accuracy = 0.252000
k = 15, accuracy = 0.289000
k = 15, accuracy = 0.278000
k = 15, accuracy = 0.282000
k = 15, accuracy = 0.274000
k = 20, accuracy = 0.270000
k = 20, accuracy = 0.279000
k = 20, accuracy = 0.279000
k = 20, accuracy = 0.282000
k = 20, accuracy = 0.285000
k = 50, accuracy = 0.271000
k = 50, accuracy = 0.288000
k = 50, accuracy = 0.278000
k = 50, accuracy = 0.269000
k = 50, accuracy = 0.266000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.270000
k = 100, accuracy = 0.263000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.263000
1
2
3
4
5
6
7
8
9
10
11
12
13
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
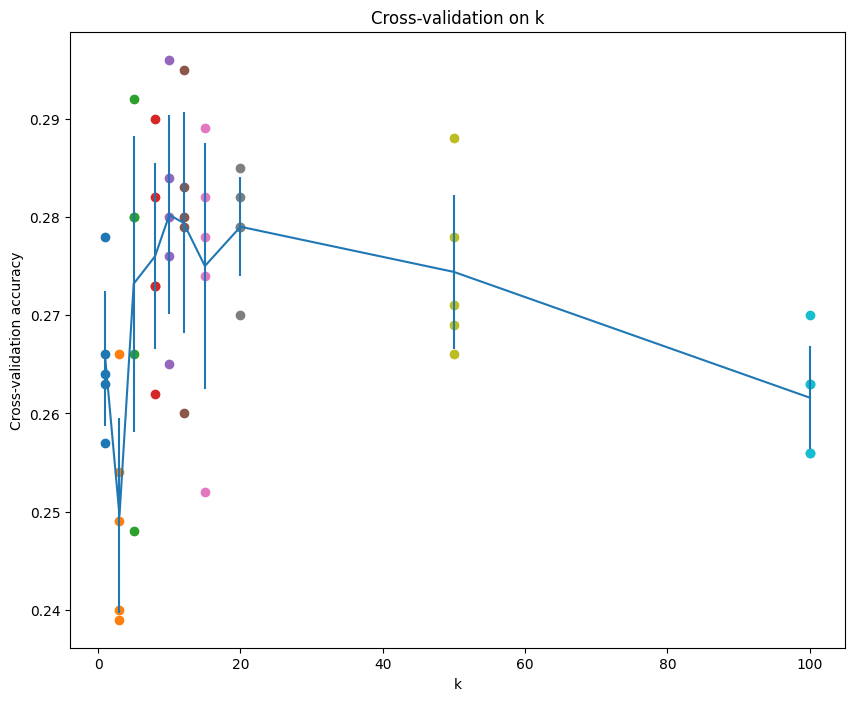
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10
# 아래 코드로도 적용 가능하다
#best_k = k_choices[accuracies_mean.argmax()]
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
1
Got 141 / 500 correct => accuracy: 0.282000
Inline Question 3
Which of the following statements about $k$-Nearest Neighbor ($k$-NN) are true in a classification setting, and for all $k$? Select all that apply.
- The decision boundary of the k-NN classifier is linear.
- The training error of a 1-NN will always be lower than or equal to that of 5-NN.
- The test error of a 1-NN will always be lower than that of a 5-NN.
- The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
- None of the above.
$\color{blue}{\textit Your Answer:}$ 2, 4
$\color{blue}{\textit Your Explanation:}$
- KNN은 비선형 분류기 이므로 그 경계는 구불구불함
- 1-NN은 자기 자신을 가장 가까운 이웃으로 선택하므로 항상 정확히 분류하기에 훈련 에러가 0. 반면, 5-NN은 다수결로 예측하기에 오분류 가능성 존재
- 1-NN은 오비피팅 되는 경우가 많음(선택지 2번의 이유로 인해). 5-NN은 여러 이웃의 다수결을 보기에 일반화 능력이 더 뛰어남. 따라서 항상 더 낮은 테스트 에러를 가지지는 않음
- K-NN은 예측 시마다 전체 훈련 데이터와 거리를 계산하므로 테스트 시간의 시간 복잡도는 $O(Nd)$($N$ : 훈련 샘플 수, $d$ : 피처 갯수)
Enjoy Reading This Article?
Here are some more articles you might like to read next: