섹션	꼭 챙길 핵심식·키워드	왜 중요한가?	읽기 강도
3.1 Norms	‖x‖₁, ‖x‖₂, 삼각부등식	입력 스케일링·정규화, L1/L2 규제 직관	★★☆
3.2 Inner Products	⟨x,y⟩, dot, SPD 행렬	SVM/GP 커널, 거리·유사도 출발점	★★★
3.3 Lengths & Distances	d(x,y)=‖x−y‖, Cauchy–Schwarz	KNN·군집·거리기반 손실	★★☆
3.4 Angles & Orthogonality	cos ω=⟨x,y⟩/(‖x‖‖y‖)	SVM margin, cosine-sim 검색	★★☆
3.5 Orthonormal Basis		PCA·SVD 직관 "축 바꾸기"	★☆☆
3.6 Orthogonal Complement	U⊥, normal vector	하이퍼플레인, 제약 조건 투영	★☆☆
3.7 Inner Product of Functions	∫ u(x)v(x)dx	커널(무한 차원 Φ) 개념 맛보기	☆☆☆
3.8 Orthogonal Projections	P= B(BᵀB)⁻¹Bᵀ, LS 해	Linear Reg., PCA 재구성 오차	★★★
3.8.3 Gram–Schmidt	uₖ = bₖ − πspan(u₁…uₖ₋₁)(bₖ)	QR분해·CG·좌표정규화	★★☆
3.9 Rotations	2D, 3D, Givens	CNN weight 공유 해석, 증강변환	★☆☆

노름(Norms)

정의

벡터 공간 $V$위의 노름은 다음과 같이 정의된다.

\[\begin{gather} \lVert \cdot \rVert : V \rightarrow \mathbb{R} \\ x \mapsto \lVert x \rVert \end{gather}\]

즉, 노름은 벡터 공간 $V$와 각 벡터$x$에 대해 그 벡터의 길이를 나타내는 실수 값 $\lVert x \rVert \in \mathbb{R}$을 반환하는 함수이다.

노름의 성질

1. 절대적 동차성(Absolute homogeneity) : $\lVert \lambda x \rVert = \lvert \lambda \rvert \cdot \lVert x \rVert$ 스칼라를 곱하면 노름도 그 절댓값만큼 스케일링 된다.

2. 삼각 부등식(Triangle inequality) : $\lVert x+y \rVert \le \lVert x \rVert + \lVert y \rVert$ 두 벡터를 더한 벡터의 노름은 각 벡터 노름의 합보다 크지 않다.

3. 양의 정부호성(Positive definiteness) : $\lVert x\rVert \ge and \lVert x\rVert = 0 \Leftrightarrow x=0$ 벡터의 노름은 0보다 크거나 같으며, 0인 경우에만 벡터가 0이다.

Manhattan Norm(L1 Norm)

실수 공간 $\mathbb{R}^n$위에 정의된 맨하탄 노름(Manhattan Norm)은 $x\in \mathbb{R}^n$에서 다음과 같이 정의된다.

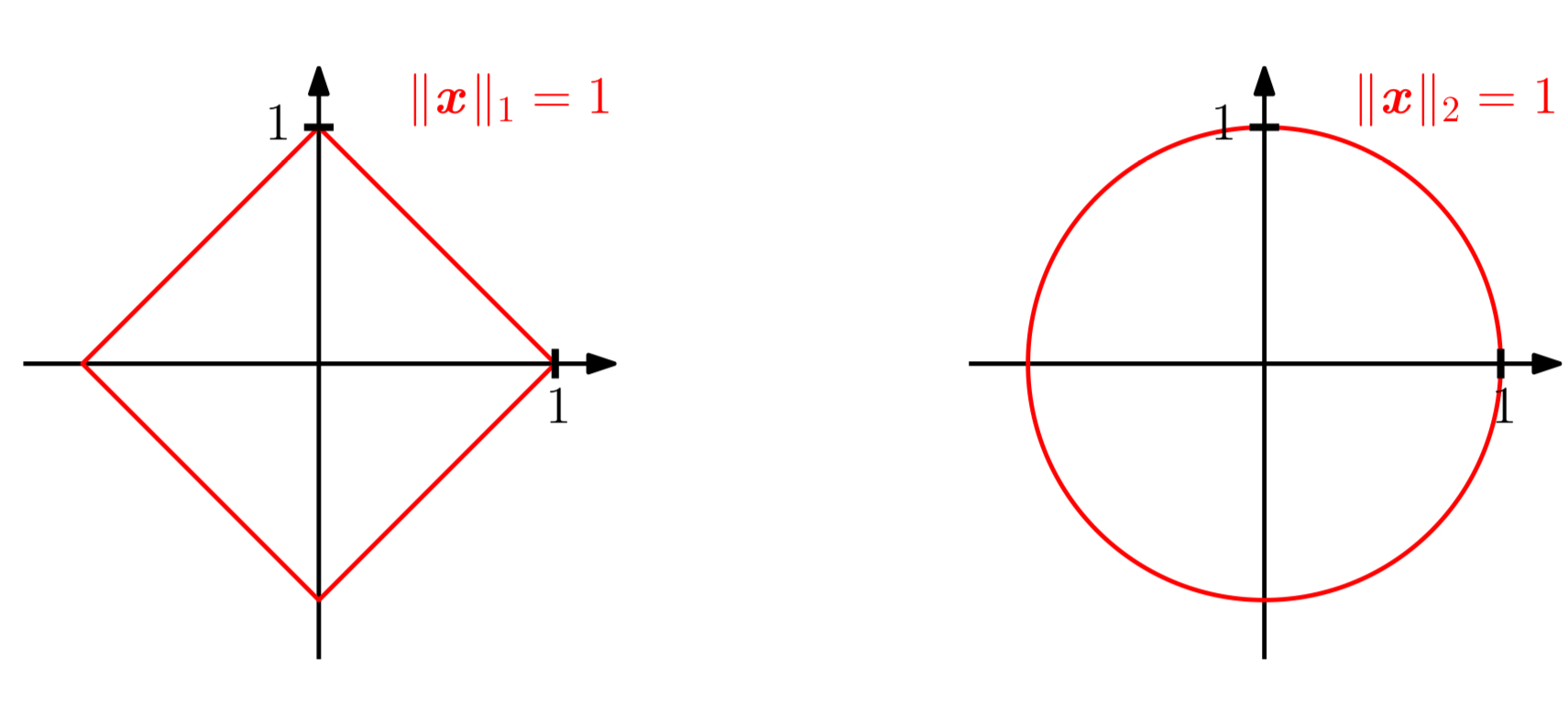
\[\lVert x \rVert_1 := \sum^n_{i=1}\lvert x_i \rvert\]

상단 그림의 좌측 이미지는 $\lVert x \rVert_1 = 1$을 만족하는 모든 $x \in \mathbb{R}^2$들을 시각화 한 것이다.

Euclidean Norm(L2 Norm)

실수 공간 $\mathbb{R}^n$위에 정의된 유클리드 노름(Euclidean Norm)은 $x\in \mathbb{R}^n$에서 다음과 같이 정의된다.

\[\lVert x \rVert_2 := \sqrt{\sum^n_{i=1}x_i^2}=\sqrt{x^\top x}\]

유클리드 노름은 원점으로부터 $x$까지의 유클리드 거리를 계산한다. 상단 그림의 우측 이미지는 $\lVert x \rVert_2 = 1$을 만족하는 모든 $x \in \mathbb{R}^2$들을 시각화 한 것이다.

내적(Inner product)

정의

벡터 공간 $V$에서 함수 $\Omega : V \times V \rightarrow \mathbb{R}$는 두 벡터를 입력받아 실수로 대응시키는 쌍선형(bilinear) 함수라고 하자. 이때 다음을 따른다.

• 모든 $x, y \in V$에 대해 $\Omega(x,y) = \Omega(y,x)$를 만족하면 $\Omega$는 대칭적(symmetric)이다.
• 다음 조건을 따르면 $\Omega$는 양의 정부호(positive definite)이다.

\[\forall x\in V \backslash \{ 0 \} : \Omega(x,x) > 0, \quad \Omega(0,0)=0\]

• 대칭적이고 양의 정부호인 쌍선형 함수 $\Omega : V \times V \rightarrow \mathbb{R}$은 $V$의 내적(inner product)이라고 부르며, 일반적으로 $\langle x,y\rangle$로 작성한다.
• 쌍 ($V,\langle \cdot,\cdot \rangle$)은 내적공간(inner product space) 또는 벡터 공간에서의 내적(vector space with inner product)라고 한다.

양의 정부호인 대칭 행렬(Symmetric, Positive Definite Matrices)

내적 공간 $V$와 $V$의 순서가 있는 기저 $B=(b_1, \ldots, b_n)$가 있다고 하자. 이때 $x,y \in V$인 모든 벡터는 기저벡터의 선형 결합으로 작성할 수 있으므로, $x=\sum_{i=1}^n\psi_ib_i,\ y=\sum_{j=1}^n\lambda_jb_j \in V$를 만족한다. 내적의 쌍선형성으로 인해 $x,y\in V$는

\[\langle x,y\rangle = \langle \sum_{i=1}^n\psi_ib_i,\sum_{j=1}^n\lambda_jb_j\rangle = \sum_{i=1}^n \sum_{j=1}^n\psi_i\langle b_i,b_j \rangle \lambda_j=\hat{x}^\top A\hat{y}\]

를 만족하고, 이때 $A_{ij}:=\langle b_i, b_j \rangle$과 $\hat{x}, \hat{y}$는 기저 $B$를 다르는 $x,y$의 좌표 벡터이다.

이는 내적 $\langle \cdot,\cdot \rangle$이 유일하게 $A$를 통해서만 정의됨을 의미한다. 또한 내적의 대칭성은 $A$ 또한 대칭임을 의미하며, 더 나아가서 내적의 양의 정부호성은 다음을 의미한다.

\[\forall x \in V \backslash\{0\} : x^\top A x> 0\]

내적의 양부호성을 만족하는 $A \in \mathbb{R}^{n\times n}$은 양의 정부호인 대칭행렬 또는 그냥 양의 정부호인 행렬이라고 부르며, 위 수식에서 $\geqslant$를 사용한다면 symmetric, positive semidefinite라고 부른다.

만약 $A \in \mathbb{R}^{n\times n}$이 양의 정부호인 대칭 행렬이라면 다음 정의는 순서가 있는 기저 $B$를 따르는 내적을 의미한다.

\[\langle x,y \rangle = \hat{x}^\top A \hat{y}\]

정리

실수 값을 가지는 유한한 차원의 벡터 공간 $V$와 그 공간의 순서가 있는 기저$B$가 있을 때 다음 명제가 성립한다

\[\langle\cdot,\cdot\rangle : V \times V \rightarrow \mathbb{R}\]

이때 위 명제가 내적이 되기 위한 필요충분 조건은, 대칭이고 양의 정부호인 행렬 $A\in\mathbb{R}^{n\times n}$가 존재하는 것이다. 동시에 내적은 다음과 같이 표현된다.

\[\langle x,y \rangle = \hat{x}^\top A \hat{y}\]

위 명제를 충족하면 다음과 같은 성질을 같는다.

• $A$의 널 공간은 오직 0으로 구성된다. 왜냐하면 모든 $x \ne 0$에 대해 $x^\top Ax>0$이기 때문이며, 이는 $x \ne 0$일때 $Ax \ne 0$임을 의미한다.
• $A$의 대각성분 $a_{ij}$는 양수이다. 왜냐하면 $a_{ii}=e_i^\top A e_i$이기 때문이다. 이때는 $e_i$는 $\mathbb{R}^n$에 속한 표준 기저벡터 중 $i$번째 벡터이다.

길이와 거리(Lengths & Distances)

일반적으로 모든 내적은 노름 $\lVert x\rVert := \sqrt{\langle x,x \rangle}$을 유도할 수 있고, 이를 통해 벡터 간의 거리를 계산할 수 있다. 그러나 모든 노름이 내적을 통해 유도되지는 않는다.

$x= [1,1]^\top \in \mathbb{R}^2$일 때 스칼라 곱을 내적으로 이용한다면 다음과 같이 $x$의 길이를 계산 할 수 있다.

\[\lVert x \rVert = \sqrt{x^\top x}=\sqrt{1^2 + 1^2} = \sqrt{2}\]

만약 다른 내적을 정의해 이용한다면 어떨까?

\[\langle x,y \rangle := x^\top \begin{bmatrix}1 & -\frac{1}{2} \\ -\frac{1}{2} & 1\end{bmatrix}y = x_1y_1 - \frac{1}{2}(x_1y_2+x_2y_1)+x_2y_2\]

벡터의 노름을 계산할 때 $x_1, x_2$가 같은 부호를 가진다고 가정하면 스칼라 곱을 사용한 방식보다 작은 값을 반환하지만, 다른 부호를 가진다고 가정하면 스칼라 곱 보다 더 큰 값을 반환한다. 위 내적을 이용해서 계산하면 다음과 같다.

\[\langle x,x\rangle = x_1^2 - x_1x_2 + x_2^2 = 1-1+1 = 1 \Rightarrow \lVert x \rVert = \sqrt{1} = 1\]

정의

내적 공간 ($V,\langle \cdot,\cdot \rangle$)에서 다음 수식은 $x,y$간의 거리(distance)를 나타낸다.

\[d(x,y) := \lVert x-y\rVert = \sqrt{\langle x-y, x-y\rangle}\]

이때 스칼라 곱을 내적으로 사용한다면 이 거리는 유클리드 거리(Euclidean distance)라고 부른다.

다음 사상은 Metric라고 부른다.

\(\begin{align} d &: V \times V \rightarrow \mathbb{R} \\ &(x,y) \mapsto d(x,y) \end{align}\) Metric은 다음 조건을 충족한다.

• 양의 정부호 : 모든 $x,y \in V$에 대해 $d(x,y) \geqslant0$이며, $d(x,y) = 0 \Leftrightarrow x=y$이다.
• 대칭성 : 모든 $x,y \in V$에 대해 $d(x,y)=d(y,x)$
• 삼각 부등식 : $x,y,z \in V$에 대해 $d(x,z) \leqslant d(x,y)+d(y,z)$

코시-슈바르츠 부등식(Cauchy-Schwarz Inequality)

내적 벡터 공간 ($V, \langle\cdot,\cdot \rangle$)이 노름 $\lVert \cdot \rVert$를 유도한다면 다음 코시 슈바르츠 부등식을 만족한다.

\[\vert \langle x,y \rangle \vert \leqslant \lVert x\rVert\lVert y\rVert\]

Remark

벡터의 길이와 마찬가지로 벡터간의 거리도 내적 없이 노름만으로 정의할 수 있다. 하지만 그 노름이 내적에 의해 유도되었다고 가정하면 거리는 어떤 내적을 사용하는지에 의존적이다.

각과 직교 (Angles & Orthogonality)

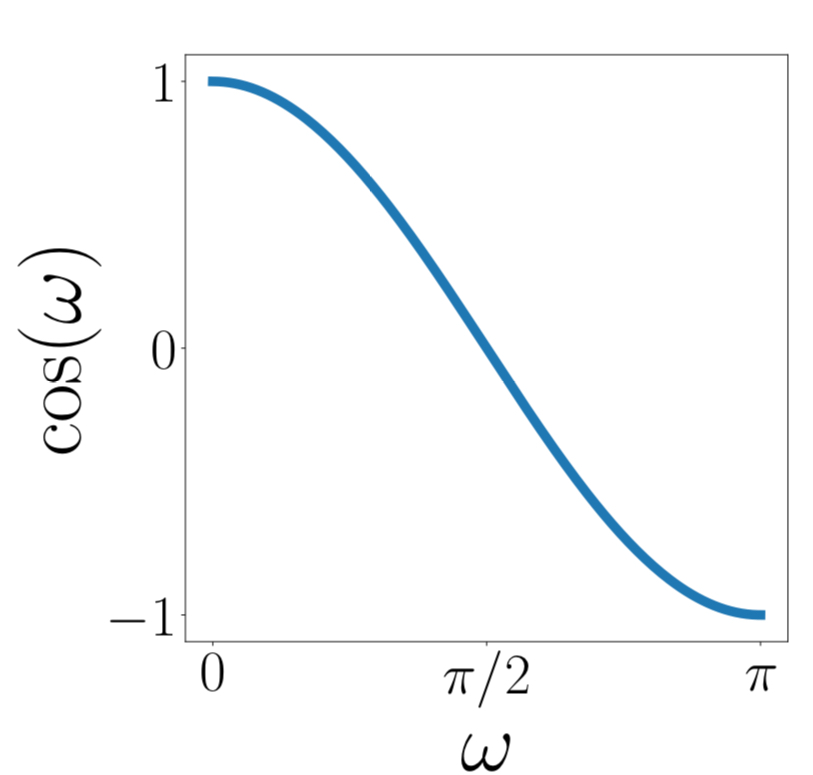
두 벡터간의 각 $\omega$를 정의함으로써 내적은 벡터공간의 기하학적 개념에도 접근할 수 있다. 상술한 코시 슈바르츠 부등식을 활용하면 다음과 같은 부등식을 도출 할 수 있다.

\[-1 \le \frac{\langle x,y\rangle}{\lVert x\rVert \lVert y\rVert} \le 1\]

따라서 유일한 $x,y$ 사이의 각$\omega \in [0,\pi]$가 존재한다.

\[\cos{\omega} = \frac{\langle x,y\rangle}{\lVert x\rVert \lVert y\rVert}=\frac{\langle x,y\rangle}{\langle x,x\rangle\langle y,y\rangle} =\frac{x^\top y}{\sqrt{x^\top x y^\top y}}\]

정의(직교성, Orthogonality)

두 벡터 $x,y$가 필요충분조건 $\langle x,y \rangle = 0$을 만족하면 직교(orthogonal)한다고 표현하며, $x \perp y$로 작성한다. 추가로 $\lVert x\rVert = \lVert y \rVert = 1$(단위벡터)이면 정규 직교(orthonormal) 하다. 위 정의를 적용하면 0벡터는 벡터 공간 상의 모든 벡터에 직교한다.

벡터의 거리와 마찬가지로 스칼라 곱이 아닌 내적을 사용하면 $\omega$는 달라질 수 있다. 여기서 알 수 있는 점은, 어떤 내적에 대해서 두 벡터가 직교하다면, 다른 종류의 내적에 대해서는 직교하지 않는다는 점이다.

정의(직교행렬, Orthogonal Matrix)

정방행렬 $A \in \mathbb{R}^{n\times n}$이 필요충분조건 ‘각 열 벡터들이 모두 단위벡터이고 서로 직교한다’를 만족하면 직교 행렬(Orthogonal matrix)라고 부르며 다음과 같이 표현할 수 있다.

\[\begin{gather} AA^\top = I = A^\top A \\ A^{-1} = A^\top \end{gather}\]

이 때 직교행렬의 역행렬은 전치하여 얻을 수 있다.

직교 행렬의 특성

직교 행렬을 이용한 벡터의 변환은 벡터의 길이를 보존한다. 수식으로는 다음과 같이 표현할 수 있다.

\[\|Ax\|^2 = (Ax)^\top (Ax) = x^\top A^\top A x = x^\top I x = \|x\|^2\]

또한 직교행렬은 두 벡터 사이의 각도도 보존한다.

\[\cos \omega = \frac{(Ax)^\top (Ay)}{\|Ax\| \cdot \|Ay\|} = \frac{x^\top y}{\|x\| \cdot \|y\|}\]

정규직교 기저(Orthonormal Basis)

정의

n차원 벡터 공간 $V$의 기저 ${b_1, \ldots,b_n}$이 다음 조건을 만족하면 이 기저는 정규 직교 기저(Orthonormal Basis, ONB)라고 부른다.

1. $\langle b_i, b_j\rangle = 0 \quad \mathbf{for} \ \ i\ne j$
2. $\langle b_i, b_i \rangle = 1$

조건 1만 만족하고 2는 만족하지 않는다면 단순 직교 기저(orthogonal basis)이다.

Gram-Schmidt Process

주어진 벡터 집합 ${\tilde{b_1}, \ldots ,\tilde{b_n}}$이 직교도 아니고 정규화도 되어있지 않은 경우 이를 정규직교 기저로 바꾸는 과정을 Gram-Schmidt Process라고 한다.

1. 벡터 집합을 행렬($\tilde{B}=[\tilde{b_1}, \ldots, \tilde{b_n}]$)로 만든다.
2. 행렬을 증강 행렬 $[\tilde{B}\tilde{B}^\top \lvert \tilde{B}]$로 만들어 가우스 소거법을 적용한다.

정규직교 기저의 예

\[b_1 = \frac{1}{\sqrt{2}}\begin{bmatrix}1\\1\end{bmatrix}, \qquad b_2 = \frac{1}{\sqrt{2}}\begin{bmatrix}1\\-1\end{bmatrix}\]

• $b_1^\top b_2 = 0 \ \rightarrow$ 직교
• $\lVert b_1\rVert=\lVert b_2\rVert = 1 \rightarrow$ 정규

직교 여공간 (Orthogonal Complement)

D차원 벡터 공간 $V$와 M차원 벡터 부분 공간 $U \subseteq V$가 있을때, 직교 여공간 $U^\bot$은 $V$의 (D-M)차원 부분공간이며, $V$의 벡터 중 $U$의 벡터에 직교하는 모든 벡터를 포함한다. 더 나아가 $U \cap U^\bot = {0}$ 이므로 공간 $V$에 포함된 모든 벡터는 다음과 같이 유일하게 분해할 수 있다.

\[x \;=\; \underbrace{\sum_{m=1}^{M}\lambda_m\,b_m}_{\text{U 성분}}       + \underbrace{\sum_{j=1}^{D-M}\psi_j\,b^{\perp}_j}_{U^{\perp}\text{ 성분}},       \qquad \lambda_m,\psi_j\in\mathbb{R}.\]

이 때 $(b_1, \ldots b_M)$은 $U$의 기저이며, $(b_1^\bot, \ldots b_{D-M}^\bot)$은 $U^\bot$의 기저이다.

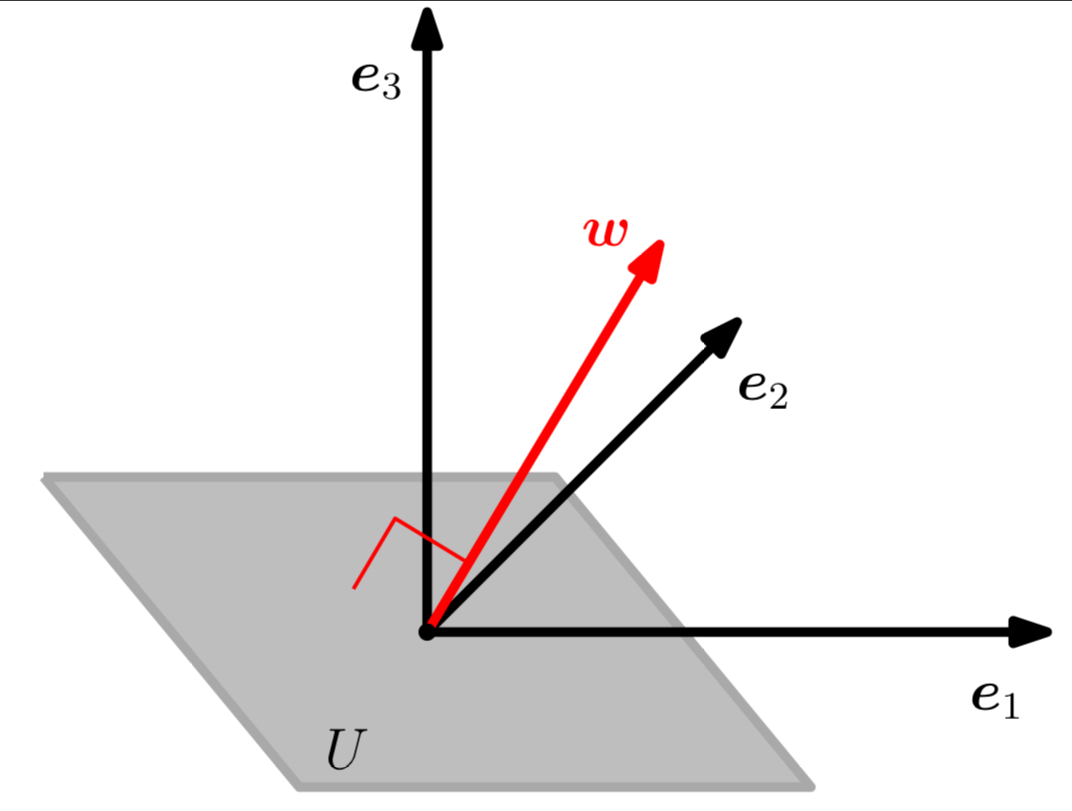
직교 여공간은 (이차원 부분 공간에 속하는) 평면 $U$를 삼차원 벡터 공간에서 표현할 수 있도록 한다. 부연 설명하자면, 평면 $U$에 직교하는 벡터 $w(\lVert w \rVert=1)$는 $U^\bot$의 유일 기저벡터이며 부호($\pm$)만 다르다. $w$에 직교하는 모든 벡터는 평면 $U$에 평행하며, 벡터 $w$는 $U$의 법선벡터 (normal vector)라고 부른다.

직교 투영 (Orthogonal Projections)

정의(투영, Projections)

벡터 공간 $V$와 그 부분공간 $U\in V$가 있다고 하자. 선형 사상 $\pi : V \rightarrow U$가 다음 조건을 만족시키면 투영(projections)이라고 한다.

\[\pi^2=\pi \circ \pi = \pi\]

위 정의는 투영 행렬(projection matrices)$P_\pi$에 적용된다.

일차원 부분공간(직선)으로의 정사영

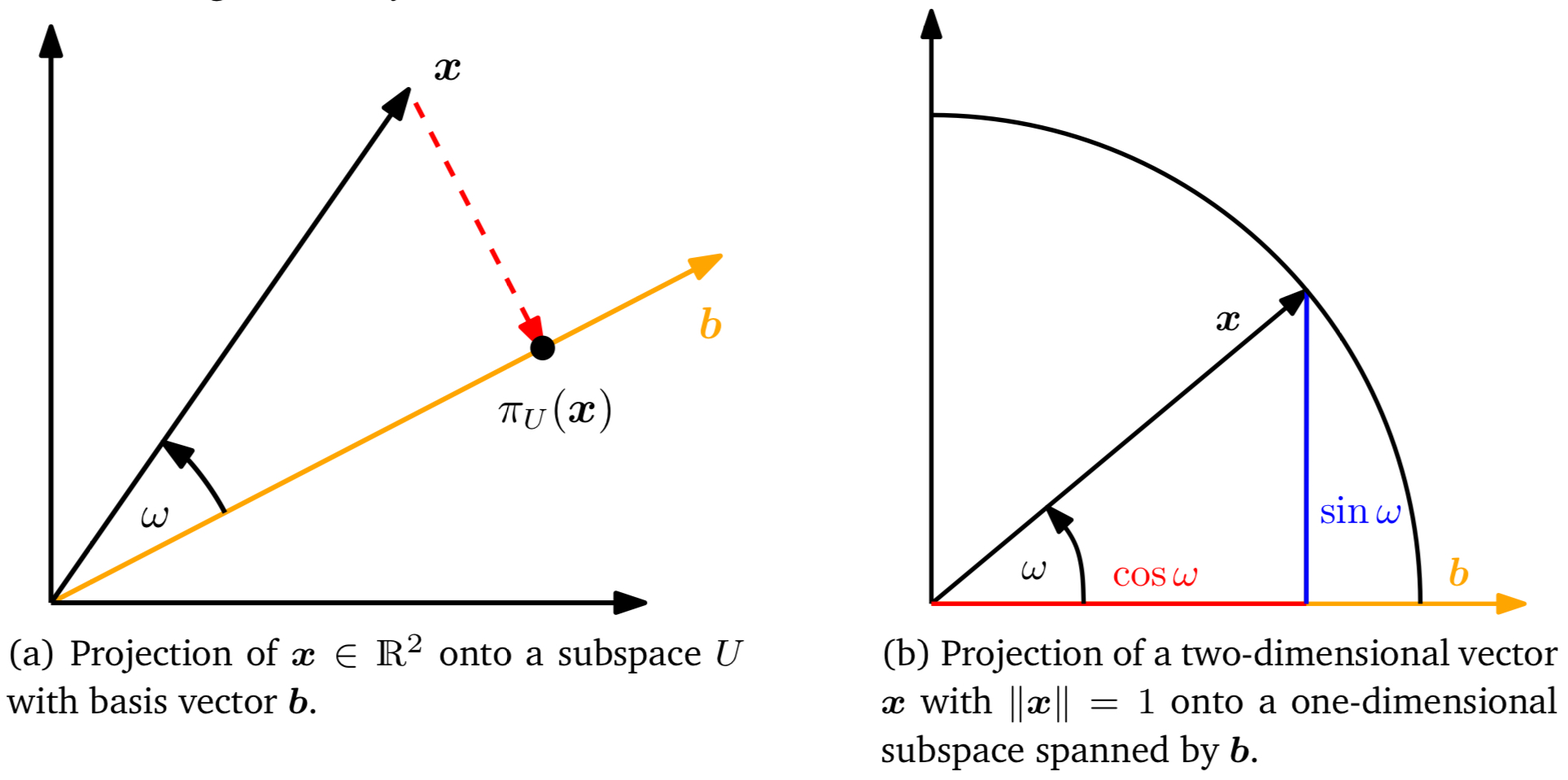
직선은 $b$에 의해 스팬되는 일차원 부분공간 $U \subseteq \mathbb{R}^n$이다. $x \in \mathbb{R}^n$을 $U$위로 정사영한다면 $x$에 가장 가까운 벡터 $\pi_U(x)\in U$를 구할 수 있다.(Figure3.4(a))

$\pi_U(x) \in U$의 특성은 다음과 같다.

• $\pi_U(x)$는 $x$와 가장 가까운 위치에 있다. ‘가까운’은 $\lVert x-\pi_U(x)\rVert$의 최소값을 가짐을 의미한다. 그 말인 즉슨, $\pi_U(x)$에서 $x$를 잇는 선분은 $U$에 직교함을 의미한다. 따라서 $\pi_U(x)$에서 $x$로의 벡터 $\pi_U(x)-x$는 $U$와 그 기저 벡터 $b$에 직교한다. 이는 $\langle \pi_U(x)-x, b\rangle=0$임을 의미한다.
• $x$의 $U$위로의 정사영 $\pi_U(x)$는 항상 $U$의 공간 안에 위치한다. 만약 $U$가 한 개의 기저 벡터 $b$로 생성된 1차원 부분공간이라면, $\pi_U(x)$는 $b$의 스칼라배 형태를 가진다.

정사영 과정

1. 계수 $\lambda$ 를 찾아보자. 직교 조건은 다음을 도출한다.

\[\langle x - \pi_U(x),b)\rangle = 0 \Leftrightarrow \langle x - \lambda b, b \rangle = 0\]

내적의 쌍선형성을 활용하여 다음 결과를 도출할 수 있다.

\[\langle x,b \rangle - \lambda \langle b,b \rangle \Leftrightarrow \lambda = \frac{\langle x,b \rangle}{\langle b,b \rangle} = \frac{\langle b,x \rangle}{\lVert b \rVert^2}\]

최종적으로 내적이 대칭적이라는 사실을 이용하면 다음 결과를 얻을 수 있다.

\[\lambda = \frac{b^\top x}{b^\top b} = \frac{b^\top x}{\lVert b \rVert^2}\]

이 때 $\lVert b \rVert=1$라면 계수 $\lambda$는 단순히 $b^\top x$로 주어진다.

1. 정사영점 $\pi_U(x) \in U$를 찾아보자. $\pi_U(x)=\lambda b$이기 때문에 바로 다음 수식을 얻을 수 있다.

\[\pi_U(x) = \lambda b = \frac{\langle x,b \rangle}{\lVert b \rVert^2}b = \frac{b^\top x}{\lVert b\rVert^2}b\]

또한 노름의 정의에 의해 $\pi_U(x)$의 길이를 계산할 수 있다.

\[\lVert \pi_U(x) \rVert = \lVert \lambda b \rVert = \lvert \lambda \rvert \lVert b \rVert\]

따라서 정사영은 $\lvert \lambda \rvert \lVert b \rVert$ 만큼의 길이를 가지게 되고, 이는 직관적으로 $\lambda$가 1차원 부분공간 $U$를 생성하는 기저벡터 $b$에 대해 정사영 $\pi_U(x)$가 갖는 좌표값임을 알 수 있다.

\[\lVert \pi_U(x) \rVert = \frac{\lvert b^\top x}{\lVert b \rVert^2} = \lvert \cos{\omega} \lVert x \rVert \lVert b \rVert \frac{\lVert b \rVert}{\lVert b \rVert^2} = \lvert \cos{\omega} \rvert \lVert x \rVert\]

이때 $\omega$는 $x,b$ 사이의 각을 의미한다. 이 수식은 삼각함수에서도 매우 익숙한 형태인데, 만약 $\lVert x \rVert = 1$이라면 $x$는 단위 원 위에 놓이게 된다. 따라서 $x$를 $b$가 생성하는 수평축 방향으로 정사영 한 결과는 $\cos{\omega}$가 되며 그 벡터의 길이도 $\lvert \cos{\omega} \rvert$가 된다. (Figure 3.10(b))

1. 투영행렬 $P_\pi$를 찾아보자. 투영은 정의에 따르면 선형 사상이므로, $\pi_U(x)=P_\pi x$와 같은 투영행렬이 존재한다.

\[\pi_U(x) = \lambda b = b \lambda = b\frac{b^\top x}{\lVert b \rVert^2} = \frac{bb^\top}{\lVert b \rVert^2}x\]

이므로 다음이 성립함을 알 수 있다.

\[P_\pi = \frac{bb^\top}{\lVert b \rVert ^2}\]

이 때, $bb^\top$은 (결과적으로는 $P_\pi$) 랭크가 1인 대칭 행렬이며, $\lVert b \rVert^2 = \langle b,b \rangle$은 스칼라 값이다. 또한 행렬 $P_\pi$는 $x \in \mathbb{R}^n$에 속하는 모든 벡터를 원점을 지나고 $b$의 방향인 선분 위로 투영한다.

알아둘 점 1

정사영 $\pi_U(x) \in \mathbb{R}^n$은 여전히 n차원 벡터이며 스칼라 값이 아니다. 반면에, 투영을 표현하기 위해 n개의 계수를 알 필요는 없어졌으며, 부분공간 $U$를 생성하는 기저벡터 $b$에 대해 표현하고자 할 때는, 단 하나의 좌표값 $\lambda$만으로 충분하다.

알아둘 점 2

$\pi_U(x)$가 $P_\pi$의 고유벡터(eigenvector)임을 보일 수 있다. 그리고 그에 대응하는 고윳값(eigenvalue)은 1이다.

임의의 부분공간으로의 정사영

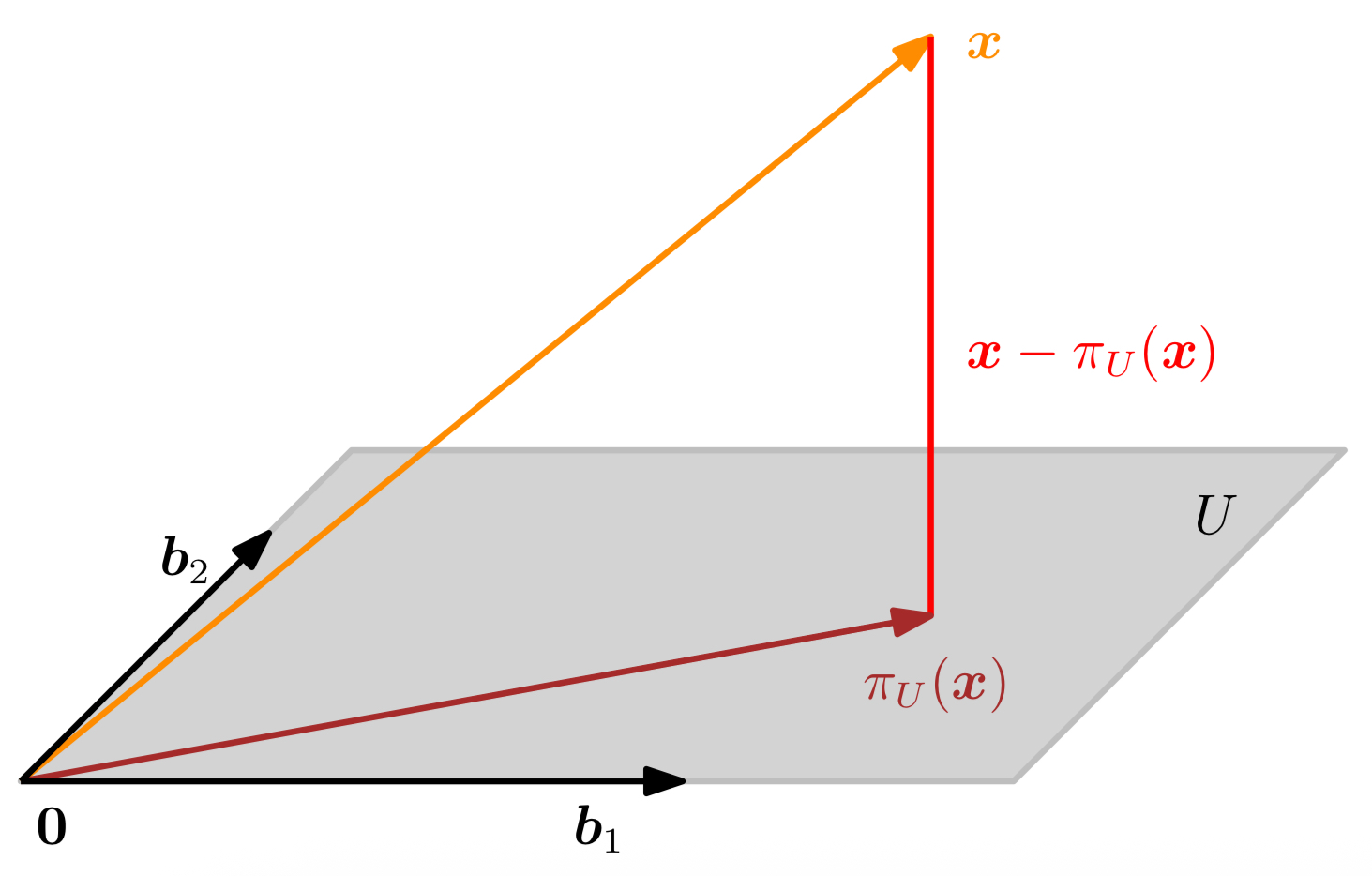
벡터 $x\in \mathbb{R}^n$가 $\dim{(U)}= m \ge 1$을 만족하는 부분공간 $U \subseteq \mathbb{R}^n$으로의 정사영을 살펴보자. 이때, $(b_1, \ldots b_m)$은 $U$의 정렬된 기저이며, $U$로의 정사영 $\pi_U(x)$는 필연적으로 $U$의 요소이다. 따라서 정사영은 $\pi_U(x)=\sum_{i=1}^m\lambda_ib_i$와 같은 기저 벡터의 결합으로 나타낼 수 있다. 이제 일차원 부분공간으로의 정사영때와 같은 삼단계 절차를 밟아 일반화 해보자.

정사영 과정

1. 정사영의 좌표 $\lambda_1, \ldots, \lambda_m$을 찾는다. 이때 다음 선형결합이 $x \in \mathbb{R}^n$에 가장 가깝도록 한다.

\[\begin{gather} \pi_U(x)=\sum^m_{i=1}\lambda_ib_i=B\lambda, \\ B = \begin{bmatrix} b_1, \ldots ,b_m\end{bmatrix} \in \mathbb{R}^{n\times m}, \qquad \lambda = \begin{bmatrix}\lambda_1, \ldots, \lambda_m \end{bmatrix} ^\top \in \mathbb{R}^m \end{gather}\]

일차원에서와 마찬가지로 ‘가장 가깝다’의 의미는 ‘최소의 거리’를 가짐을 의미한다. 이는 $\pi_U(x) \in U$와 $x \in \mathbb{R}^n$을 연결하는 벡터가 모든 $U$의 기저벡터의 수직이어야 함을 의미한다. 따라서, $m$개의 동시 조건(simultaneous conditions)을 얻게된다.

\[\begin{gather} \langle b_1, x-\pi_U(x)\rangle = b_1^\top(x-\pi_U(x)) = 0 \\ \vdots \\ \langle b_m, x-\pi_U(x)\rangle = b_m^\top(x-\pi_U(x)) = 0 \end{gather}\]

이 때, $\pi_U(x) = B\lambda$를 다음과 같이 적용할 수 있다.

\[\begin{gather} b_1^\top(x-B\lambda) = 0 \\ \vdots \\ b_m^\top(x-B\lambda) = 0 \end{gather}\]

따라서 다음과 같이 동차 선형 방정식을 구할 수 있다.

\[\begin{align} \begin{bmatrix}b_1^\top \\ \vdots \\ b_m^\top\end{bmatrix}\begin{bmatrix}x-B\lambda\end{bmatrix} = 0 & \Leftrightarrow B^\top(x-B\lambda) = 0 \\ & \Leftrightarrow B^\top B\lambda = B^\top x \end{align}\]

위 수식의 마지막 표현법을 법선 방정식(normal equation)이라고 한다. $U$의 기저벡터들은 선형 독립이기에 $B^\top B \in \mathbb{R}^{m\times m}$은 역행렬 계산이 가능한 가역행렬이다.

\[\lambda = (B^\top B)^{-1}B^\top x\]

행렬 $(B^\top B)^{-1}B^\top$은 $B$의 유사 역행렬(pseudo-inverse)이라고 부르며, 정방행렬이 아닌 행렬 $B$를 계산하는데 사용된다.

1. 정사영 $\pi_U(x) \in U$를 찾는다. 이미 $\pi_U(x)=B\lambda$임을 알고있으므로 다음과 같다.

\[\pi_U(x) = B(B^\top B)^{-1} B^\top x.\]

1. 투영 행렬 $P_\pi$를 찾는다. 2번의 식에서 $P_\pi x = \pi_U(x)$를 풀 수 있는 투영 행렬은 다음만이 유일하게 존재한다.

\[P_\pi = B(B^\top B)^{-1}B^\top\]

알아둘 점 1

임의의 부분공간으로의 사영의 해는 일차원 공간의 경우를 특수한 경우로서 내포하고 있다. 만약 $\dim(U)=1$이라면 $B^\top B \in \mathbb{R}$은 상수이며 투영행렬을 $P_\pi = \frac{BB^\top}{B^\top B}$로 쓸 수 있으며 일차원 부분공간으로의 정사영과 정화하게 일치한다.

알아둘 점 2

정사영 $\pi_U(x)$는 m차원 부분공간 $U\subseteq\mathbb{R}^n$ 안에 속해있지만 동시에 $R^n$에 속해있는 벡터이기도 하다. 다만, 정사영된 벡터를 표현하기 위해서는 $U$의 기저 벡터 $b_1, \ldots, b_m$에 대한 m개의 좌표 $\lambda_1, \ldots, \lambda_m$만으로도 충분하다.

알아둘 점 3

정사영은 해가 존재하지 않는 선형 시스템 $Ax = b$에 대해 문제를 해석하고 근사 해를 구하는 방법을 제공한다. 이 말인 즉슨, 벡터 $b$는 $A$의 열에 의해 스팬되는 부분공간 안에 위치하지 않음을 의미한다. 그 점을 감안할 때, 선형 방정식을 정확하게 풀 수는 없지만, 근사 해(approximate solution)을 찾을 수는 있다. 그 방법은 $A$의 열에 의해 스팬된 부분공간의 벡터 중 $b$와 가장 가까운 것을 찾는것이다. 이때, $b$를 $A$의 열로 생성된 부분공간에 직교 투영한 벡터를 통해 구한 해를 최소 제곱 해(least-squares solution)라고 부른다.

알아둘 점 4

벡터 $x$의 기저 벡터 {$b_1, \ldots, b_k$}를 가지는 부분공간 $U$로의 정사영을 살표보았는데, 이때 이 기저는 ONB(Orthonomal Basis, 정규직교 기저, 각과 직교의 적교성에 대한 정의 참고)이다. 따라서 정사영 방정식은 다음과 같이 간단하게 작성할 수 있다.

\[\pi_U(x) = BB^\top x\]

이때, $B^\top B = I$는 좌표벡터를 포함하기 때문에 다음이 성립한다.

\[\lambda = B^\top x\]

그 말인 즉슨, 더이상 정사영 과정에서 정사영 $\pi_U(x) \in U$을 계산하는 대신, 단순한 행렬 곱으로 정사영을 구할 수 있어 계산량이 줄어듦을 의미한다.

그람-슈미트 직교화(Gram-Schmidt Orthogonalization, 중요!!)

그람-슈미트 직교화는 n차원 벡터 공간 $V$의 모든 기저 $(b_1, \ldots, b_n)$를 $V$의 직교 혹은 정규직교 기저 $(u_1, \ldots, u_n)$로 변환이 가능하다. 이 기저는 항상 존재하며, 동일한 부분공간을 생성한다$span\begin{bmatrix} b_1, \ldots, b_n\end{bmatrix} = span\begin{bmatrix} u_1, \ldots, u_n \end{bmatrix}$. 그람-슈미트 직교화는 $V$의 어떤 기저 $(b_1,\ldots,b_n)$에서든 직교 기저 $(u_1,\ldots,u_n)$을 반복적으로 구성할 수 있다.

\[\begin{align} u_1 &:= b_1 \\ u_k &:= b_k-\pi_{span\begin{bmatrix}u_1,\ldots,u_{k-1}\end{bmatrix}}(b_k), \qquad k=2,\ldots,n \end{align}\]

위 수식에서는 $k$번째 기저벡터 $b_k$는 $k-1$번째로 구성된 직교 벡터 $u_1,\ldots,u_{k-1}$에 의해 스팬된 부분공간으로 투영되고있다. 이 투영을 기저 벡터 $b_k$에서 빼면, 기존 직교 벡터들과 수직인 새로운 벡터 $u_k$를 얻게 된다. 이 과정을 모든 $n$개의 기저 벡터 $b_1,\ldots,b_n$에 대해 반복하면 벡터 공간 $V$의 직교 기저 $u_1, \ldots, u_n$을 얻을 수 있다. 최종적으로 각 $u_k$를 정규화하여 $\lVert u_k \rVert=1$이 되도록 하면 ONB를 얻게 된다.

예시

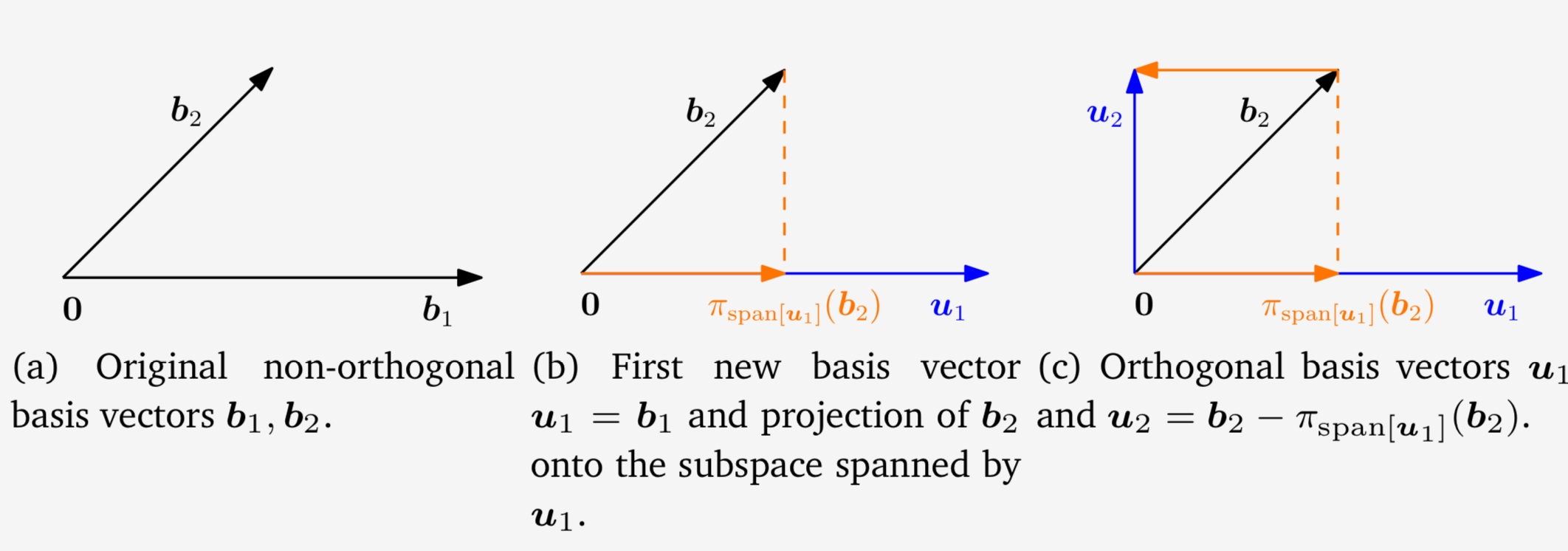
기저 $b_1, b_2 \in \mathbb{R}^2$이 다음과 같다고 가정하자.

\[b_1 = \begin{bmatrix} 2 \\ 0\end{bmatrix}, \quad b_2=\begin{bmatrix} 1 \\ 1\end{bmatrix}\]

(a)에 그람-슈미트 직교화를 적용하면 다음과 같은 직교 기저 $(u_1,u_2) \in \mathbb{R}^2$를 구성할 수 있다.

\[\begin{align} u_1 &:= b_1 = \begin{bmatrix} 2 \\ 0\end{bmatrix}, \\ u_2 &:= b_2-\pi_{span\begin{bmatrix}u_1\end{bmatrix}}(b_2) = b_2 - \frac{u_1u_1^\top}{\lVert u_1 \rVert^2}b_2 = \begin{bmatrix} 1 \\ 1\end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 0 & 0\end{bmatrix}\begin{bmatrix} 1 \\ 1\end{bmatrix} = \begin{bmatrix} 0 \\ 1\end{bmatrix} \end{align}\]

위 과정은 그림의 (b), (c)와 같고 $u_1,u_2$가 직교함을 알 수 있다.

아핀 부분공간으로의 정사영

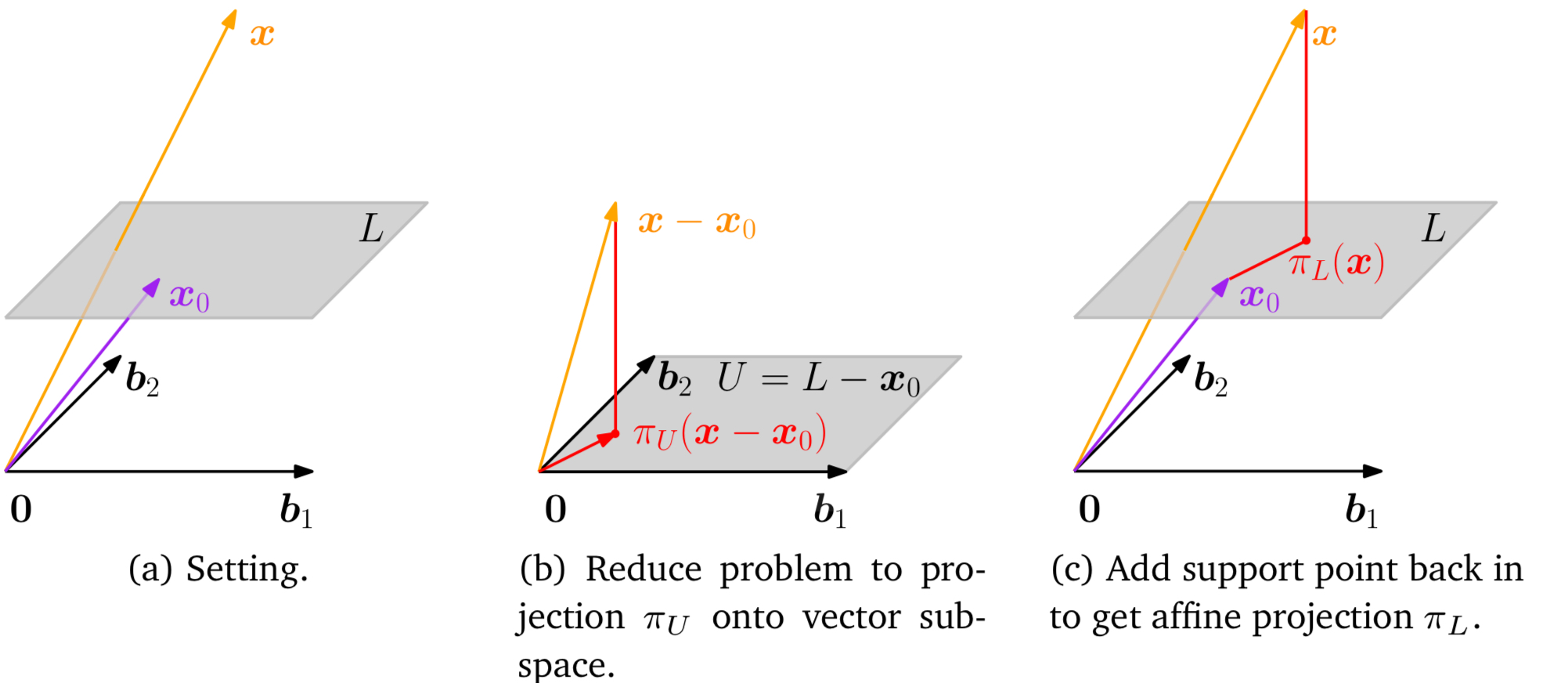
$b_1, b_2$를 기저 벡터로 가지는 $U$의 아핀 공간 $L=x_0+U$가 있다고 하자. $x$의 $L$로의 투영 $\pi_L(x)$를 정의하기 위해서 벡터 부분공간으로의 투영을 거칠 수 있다(Figure b.). 기준점 $x_0$를 벡터 $x$와 공간 $L$에서 각각 빼줌으로써, $L-x_0=U$가 정확히 벡터 부분공간 $U$가 되도록 만들 수 있다.

이제 상술하였던 부분공간으로의 정사영을 활용해서 $\pi_U(x-x_0)$를 얻을 수 있고, 이 정사영은 $x_0$를 더해줌으로써 아핀 부분공간 $L$로 다시 변환할 수 있다.

\[\pi_L(x) = x_0 + \pi_U(x-x_0)\]

이때 $\pi_u(\cdot)$은 부분공간 $U$로의 직교 투영이다.

위 그림에서 알 수 있듯 아핀 공간 $L$과 $x$의 사이의 거리는 벡터 $x-x_0$와 부분공간 $U$ 사이의 거리와 동일함이 자명하다.

\[\begin{align} d(x,L) &= \lVert x - \pi_L(x)\rVert = \lVert x-(x_0+\pi_u(x-x_0))\rVert \\ &= d(x-x_0, \pi_U(x-x_0)) = d(x-x_0, U) \end{align}\]

회전 (Rotations)

거리와 각의 보존은 직교 변환 행렬을 사용하는 선형 사상의 주요한 특징 중 하나이다.

회전(rotation, 더 정확하게는 유클리드 벡터 공간의 자기 동형 사상)은 원점으로부터 $\theta$만큼 평면을 회전시킨다. 추가로, 양의 회전각 $\theta > 0$는 일반적으로 반시계 방향으로의 회전이다.

2차원 공간($\mathbb{R}^2$)에서의 회전

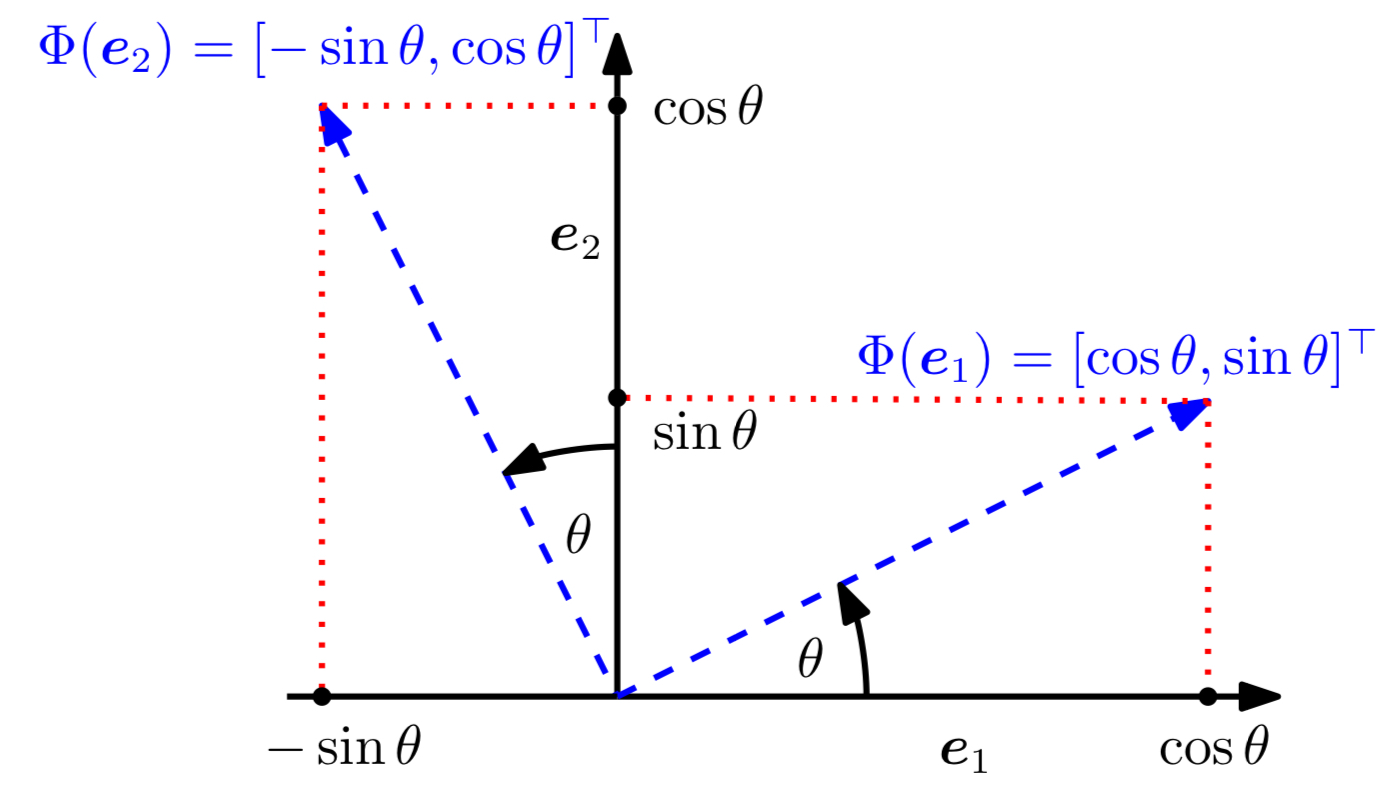
$\mathbb{R}^2$의 표준 좌표 공간을 정의하는 표준 기저 $\left\lbrace e_1 = \begin{bmatrix}1 \ 0\end{bmatrix} ,e_2=\begin{bmatrix}0 \ 1 \end{bmatrix} \right\rbrace$가 있다고 하자. 위 그림에서 보듯이 좌표계를 $\theta$만큼 회전하는 방법을 알아보자. 이때, 회전된 벡터는 여전히 선형독립이므로, $\mathbb{R}^2$의 기저이며, 이는 회전이 기저 변환을 수행함을 의미한다.

회전 사상 $\Phi$는 선형 변환이므로 회전 행렬 $R(\theta)$를 통해 표현할 수 있다. 삼각함수를 통해 회전된 축들의 좌표를 표준 기저에 대한 성분으로 계산할 수 있다.

\[\Phi(e_1)=\begin{bmatrix}\cos{\theta} \\ \sin{\theta}\end{bmatrix}, \quad \Phi(e_2)=\begin{bmatrix}-\sin{\theta} \\ \cos{\theta}\end{bmatrix}\]

따라서, 기저 변환을 수행하는 회전 행렬 $R(\theta)$는 다음과 같다.

\[R(\theta)=\begin{bmatrix} \Phi(e_1) \quad \Phi(e_2) \end{bmatrix} = \begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix}\]

3차원 공간($\mathbb{R}^3$)에서의 회전

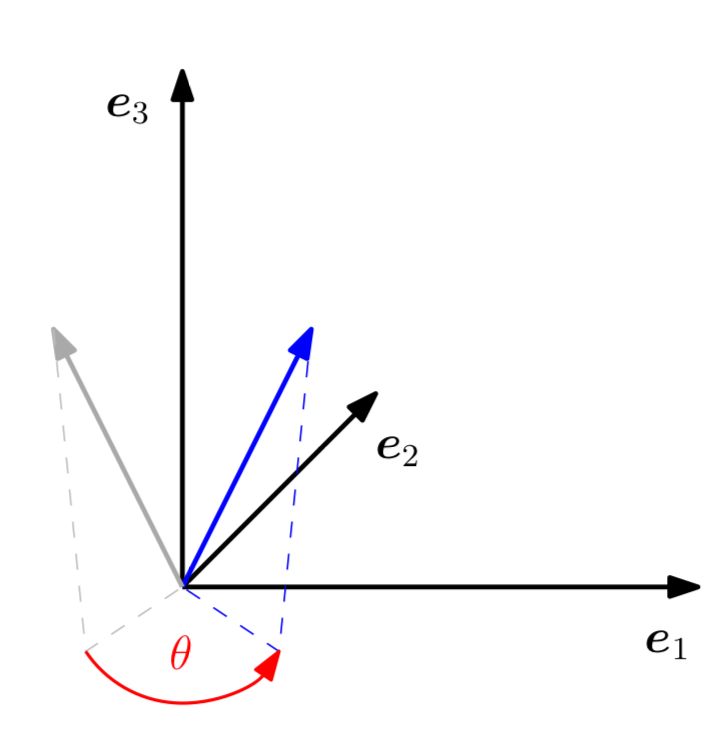
2차원 공간의 경우와는 대조적으로, 3차원 공간에서는 어떤 2차원 평면이드 1차원 축을 중심으로 회전시킬 수 있다. 가장 쉬운 방법은 표준 기저 $e_1,e_2,e_3$를 가지는 상이 어떻게 회전되는지 정의하고, 이 이미지들 $Re_1, Re_2, Re_3$가 각각 서로에게 정규 직교 하는지를 확인하는 것이다. 이 과정을 거친 후 표준 기저를 가지는 이미지들을 합쳐 표준 회전 행렬 $R$을 구할 수 있다.

의미 있는 회전 각을 가지기 위해서는, 2차원 이상의 공간에서 작업할 때 ‘반시계 방향’이 무엇을 의미하는지를 정의해야 하며, 관례적으로 반시계 방향의 회전은 축을 “끝에서 원점 방향으로” 바라보았을 때 그 축을 중심으로 하는 회전을 의미한다.

• $e_1$축의 회전

\[R_1(\theta) = \begin{bmatrix} \Phi(e_1) & \Phi(e_2) & \Phi(e_3) \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{bmatrix}\]

위 회전에서 $e_1$ 좌표는 고정되어 있고, $e_2e_3$ 평면에 대한 반시계 방향으로의 회전이 수행되고 있다.

• $e_2$축의 회전

\[R_2(\theta) = \begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\ 0 & 1 & 0 \\ -\sin{\theta} & 0 & \cos{\theta} \end{bmatrix}\]

$e_1e_3$ 평면을 $e_2$ 축에 대해 회전시키려면, $e_2$ 축을 끝점에서 시작해 원점을 향해 바라보는 시점에서 바라보아야 한다.

• $e_3$축의 회전

\[R_3(\theta) = \begin{bmatrix} \cos{\theta} & -\sin{\theta} & 0 \\ \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

그림 3.9와 같다.

$n$차원 공간에서의 회전

2차원과 3차원 회전을 $n$차원 유클리드 벡터 공간으로 일반화하는 것은, 직관적으로 ‘$n-2$’개의 차원을 고정시키고, $n$차원 공간 내의 2차원 평면에서만 회전을 수행하는 것으로 설명할 수 있다.

정의(Givens Rotation)

$V$를 $n$차원 유클리드 벡터 공간, 사상 $\Phi : V \rightarrow V$를 자기동형사상이라고 하자. 이때, 회전 행렬은 다음과 같은 구조를 가지며 $1\le i < j \le n$이며, $\theta \in \mathbb{R}$이다.

\[R_{ij}(\theta) := \begin{bmatrix} I_{i-1} & 0 & \cdots & \cdots & 0 \\ 0 & \cos\theta & 0 & -\sin\theta & 0 \\ 0 & 0 & I_{j-i-1} & 0 & 0 \\ 0 & \sin\theta & 0 & \cos\theta & 0 \\ 0 & \cdots & \cdots & 0 & I_{n-j} \end{bmatrix} \in \mathbb{R}^{n \times n}\]

위 조건을 만족하는 행렬 $R_{ij}(\theta)$를 기븐스 회전 행렬(Givens rotation)라고 한다. 본질적으로 $R_{ij}(\theta)$는 $r_{ii}=\cos{\theta}, \quad r_{ij} = -\sin{\theta}, \quad r_{ji}=\sin{\theta}, \quad r_{jj} = \cos{\theta}$와 결합된 항등행렬 $I_n$이다. 특수한 경우로, 2차원 공간에서의 기븐스 회전은 상술한 일반적은 2차원 회전 행렬과 같아진다.

회전의 성질

• 회전은 거리를 보존한다.
• 회전은 회전각을 보존한다.
• 3 이상의 차원에서의 회전은 교환법칙이 성립하지 않는다. 예외적으로 오직 2차원 벡터의 회전만이 교환법칙이 성립한다. 모든 $\phi, \theta \in [0,2\pi)$에 대해 $R(\phi)R(\theta) = R(\theta)R(\phi)$ 이다. 또한 이들이 같은 점을 중심으로 회전할 때만, 곱셈에 대해 아벨리안 군을 이룬다.