Unsupervised Learning
지도 학습(Supervised Learning)의 훈련 데이터는 입력 데이터와 정답 레이블이 쌍을 이루어 입력된다. 반면, 비지도 학습(Unspervised Learning)은 정답 레이블 없이 입력 데이터만 단일로 입력된다.
Clustering
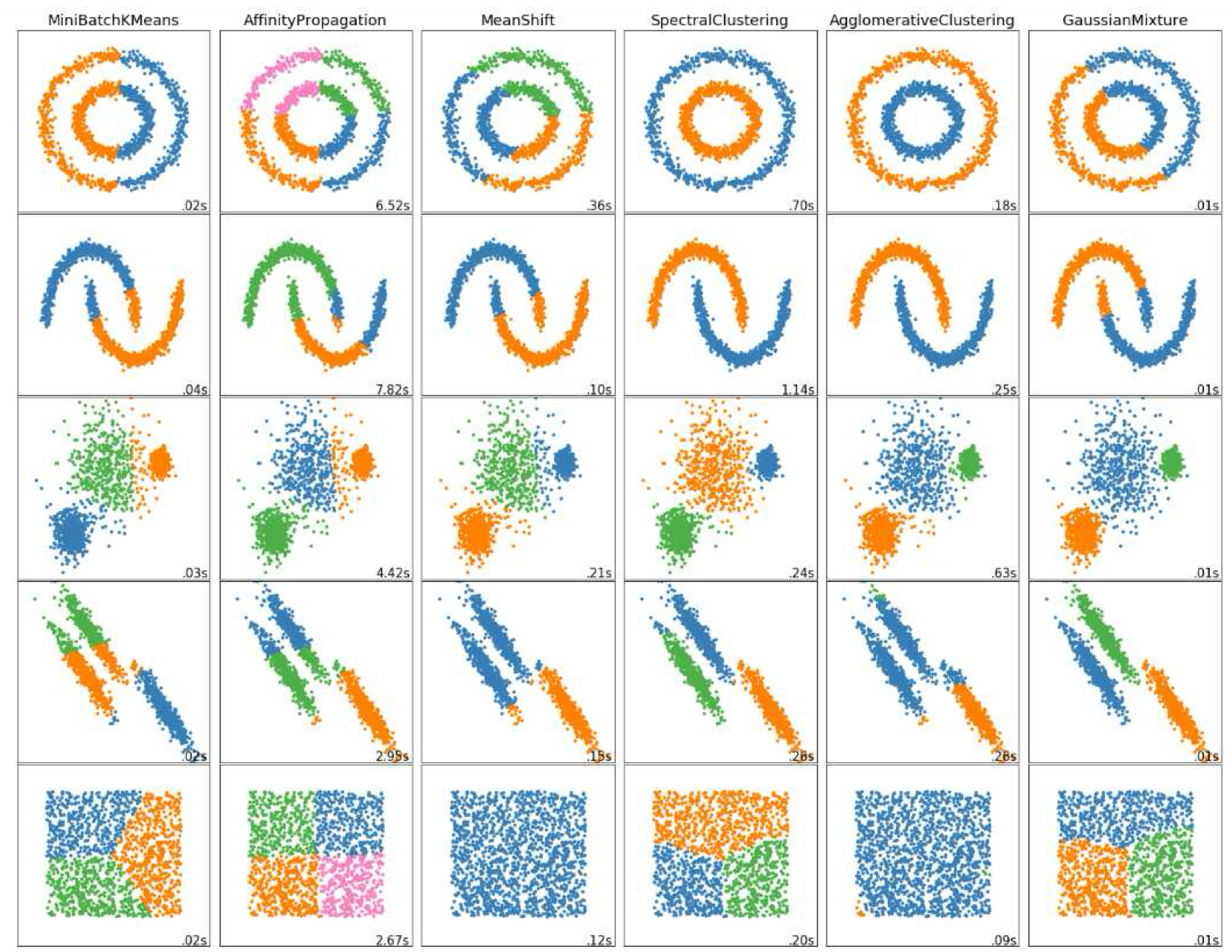
클러스터링은 유사성에 기반하여 데이터를 유사한 집합으로 나누는 방법이다. 통계학에서는 이를 **군집 분석(cluster analysis)이라고 하며, Affinity propagation, spectral clustering 등 다양한 알고리즘이 연구되어있다. 초창기에는 히스토그램 기반 분할이나 병합 방식이 주로 사용되었으며, 최근에는 거리 기반 연결, 확률 모델(K-means, GMM), 비모수 방식(Mean-shift) 등이 영상 분할에 적용되고 있다.
Classical way
클래식한 클러스터링 기밥으로는 분할(divisive) 접근과 병합(region merging) 접근을 꼽을 수 있다. 분할 접근은 이미지를 점점 더 작은 영역으로 나누는 방식이다. 이미지 조각의 히스토그램을 분석해 임계값을 기준으로 이미지를 반복적으로 세분화하며, 비슷한 영역은 나누고 다르면 유지한다. 병합 접근은 작은 영역을 유사도 기반으로 병합해 큰 영역을 만드는 방식이다.
Modernized way
연결 기반(Linkage-based) 클러스터링은 거리 기반 연결 방식이다. 고전적인 방식에 추가적으로 확률 모델을 도입해 더 유연한 클러스터링을 수행한다.
Mean-shift는 대표적인 비모수(non-parametric)방식이며, 데이터 분포를 부드럽게 만들어 피크 지점을 탐색한다.
K-means / Gaussian Mixture는 모수적(parametric) 방식이며 데이터를 소수의 정규분포로 가정하고 각 클러스터를 중심화하고 분산을 추정한다.
K-means and Gaussians mixture models
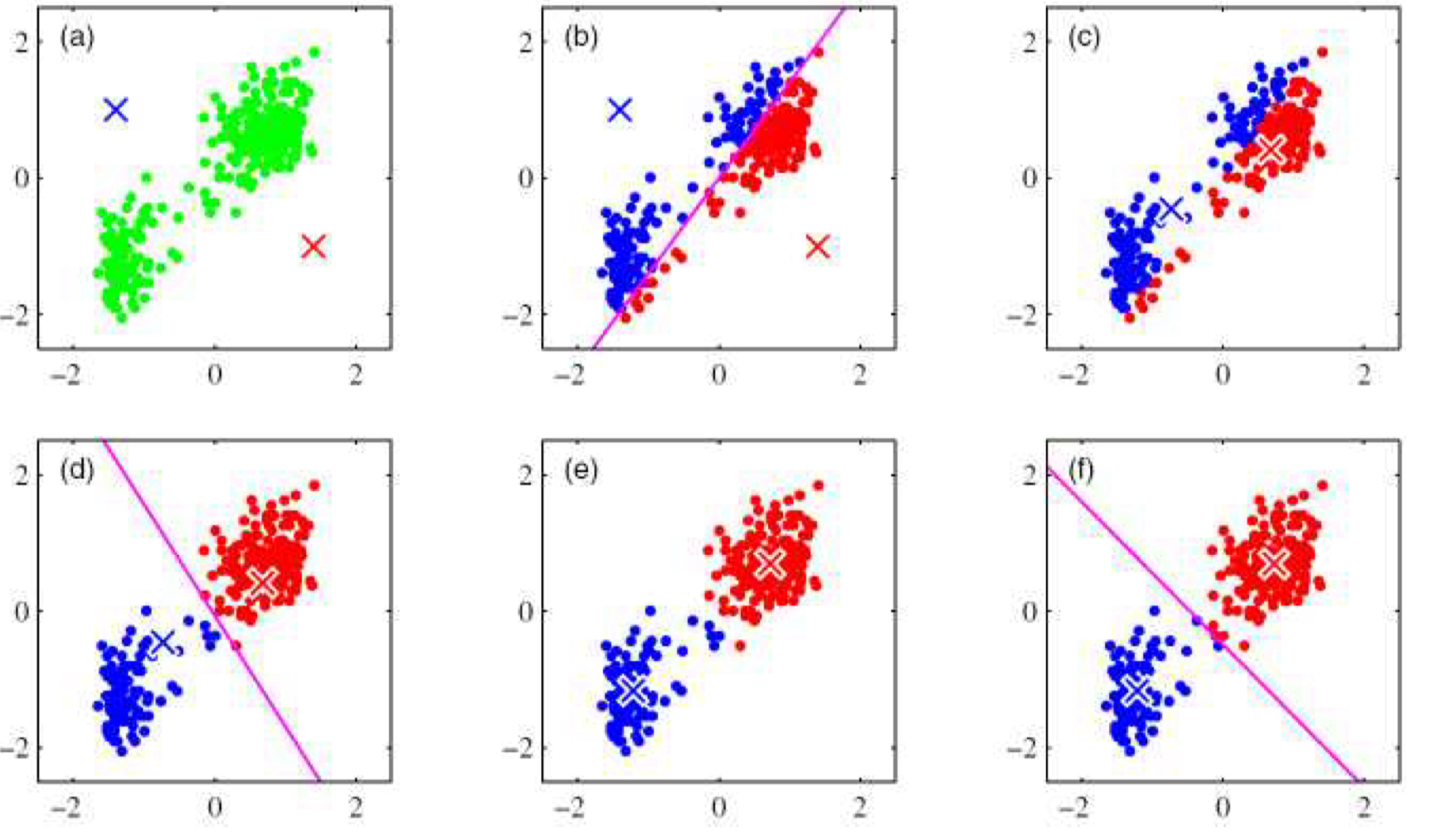
K-means는 확률 밀도를 대칭의 구 형태 분포의 중첩으로 모델링한다. 이 과정에서 명시적인 확률 모델이나 추론은 불필요하다. 대신, K-means 알고리즘은 찾고자 하는 클러스터의 개수 $k$를 입력받아 입력 피처 벡터들로부터 무작위로 $k$개의 중심을 초기화한다. 일련의 과정을 거친 후 각 샘플이 가장 가까운 중심에 할당되는 것을 목표로 클러스터 중심을 반복적으로 업데이트 한다.
또한, 각 클러스터의 통계에 기반해 중심을 분할하거나 병합하는 기술들이 개발되어 있으며, 최근접 평균 중심을 더 빠르게 찾기 위한 기술도 존재한다.
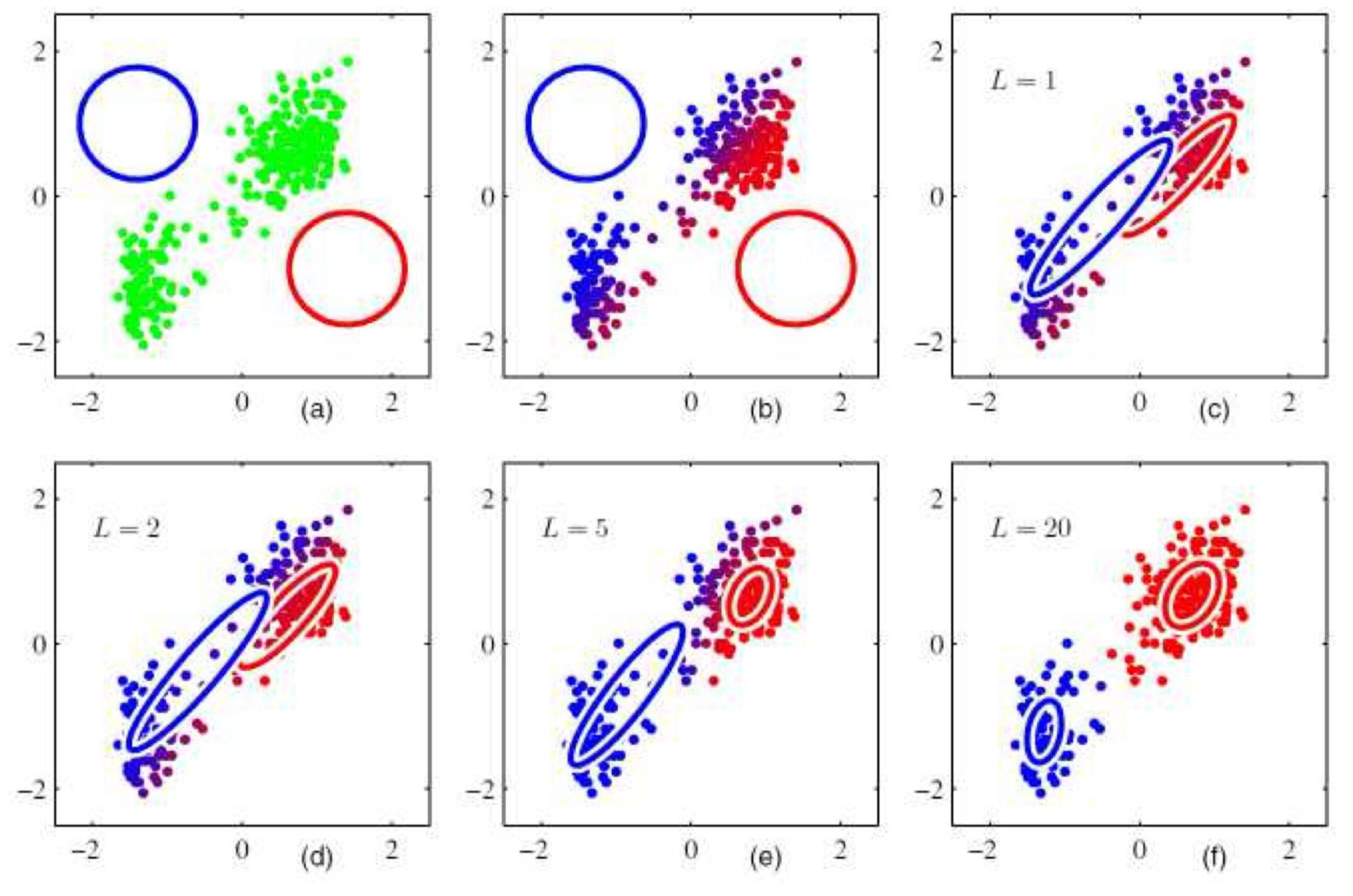
가우시안 혼합 모델에서 각각의 클러스터 중심은 해당 클러스터에 속하는 샘플들로부터 다시 추정되는 공분산 행렬에 의해 확장된다.
한 가지 예로 클러스터의 중심과 입력 샘플을 대응되게 하기 위해 nearest neighbor를 사용하는 대신 Mahalanobis distance를 사용할 수 있다.
\[d(\mathbf{x}_i;\mu_i;\Sigma_k) = \lVert \mathbf{x}_i - \mu_k \rVert_{\Sigma_k^{-1}}=(\mathbf{x}_i - \mu_k)^\top\Sigma_k^{-1}(\mathbf{x}_i - \mu_k)\]이 때, $\mathbf{x}i$는 입력 샘플, $\mu_k$는 클러스터 중심, $\Sigma_k$는 클러스터 중심과 입력 샘플의 공분산 추정을 의미한다. 입력 샘플들은 가장 근접한 클러스터 중심에 할당되거나(_hard assignment) 근처의 여러 클러스터에 할당될 수 있다(softly assignment).
후자의 방법이 더 일반적으로 사용되는데, 이는 가우시안 혼합 모델(Gaussian Mixture Model, GMM)의 파라미터를 반복적으로 재추정하는 과정에 해당한다.
\[\mathcal{p}(\mathbf{x}\vert\lbrace \pi_k,\mu_k,\Sigma_k\rbrace) = \sum_k\pi_k\mathcal{N}(\mathbf{x}\vert\mu_k,\Sigma_k)\]이 때, $\pi_k$는 혼합 계수(mixing coefficient), $\mu_k, \Sigma_k$는 가우스 평균과 공분산이다. 또한 가우스 분산은 다음과 같다.
\[\mathcal{N}(\mathbf{x}\vert\mu_k,\Sigma_k) = \frac{1}{\lvert\Sigma_k\rvert}e^{-d(\mathbf{x},\mu_k;\Sigma_k)}\]미지의 혼합 모델의 파라미터 $\lbrace\pi_k,\mu_k,\Sigma_k\rbrace$에 대한 최우도 추정값(maximum likely estimate)을 반복적으로 계산하기 위해 _EM(Expectation Maximization)_알고리즘을 수행할 수 있다.
- expectation(E step)에서는 확률을 추정한다.
이 확률은 $k$번째 가우스 클러스터에서 생성된 샘플 $\mathbf{x}_i$가 얼마나 유사한지 추정한다.
- maximization(M step)에서는 파라미터를 업데이트한다.
이 때, $N_k$는 각 클러스터에 할당된 샘플 포인트의 수를 추정한다.
Principal component analysis

앞서 혼합 모델 분석에서 보았듯이 클러스터 내의 샘플들을 다변량 가우스(multivariate Gaussian) 모델은 분포의 포착에 효과적이지만, 샘플 공간의 차원이 상승할수록 전체 공분산을 추정하는 것은 불가능에 가까워진다.
그림 5.15을 예로 들어보자. 이미지가 $P$개의 픽셀로 이루어져 있다면 공분산 행렬은 $P \times P$의 크기를 가진다. 이때 다행히도 전체 공분산을 모델링할 필요가 없는 경우가 많다. 왜냐하면, 주성분 분석(Principal Component Analysis, PCA)를 사용하면 더 낮은 랭크의 근사치 추정이 가능하기 때문이다.
Eigenface(고유얼굴)
고유얼굴(Eigenface) 기법은 임의의 얼굴 이미지 $\mathbf{x}$는 평균 얼굴 이미지 $\mathbf{m}$을 시작점으로 하고, 적은 수의 부호가 있는 기저 이미지 $\mathbf{u}_i$를 스케일링하여 더함으로써 압축 및 재구성이 가능하다는 사실에 기반한다.
\[\tilde{\mathbf{x}} = \mathbf{m} + \sum_{i=0}^{M-1}a_i\mathbf{u}_i \tag{5.7}\]이 때, 기저 이미지 $\mathbf{u}_i$(그림 5.15(a))는 학습 이미지 집합으로부터 주성분 분석을 통해 추출된다. 이 기법은 고유값 분해(Eigenvalue Analysis)라고 불린다. 연구에 따르면고유얼굴의 계수 $a_i$는 그 자체로 빠른 이미지 매칭 알고리즘을 구성하는 데 사용할 수 있다.
세부적으로 들어가면, 훈련 이미지의 집합$\lbrace \mathbf{x}_j \rbrace$로부터 시작해 이 집합으로부터 평균 이미지 $\mathbf{m}$과 산포 행렬(scatter matrix) 또는 공분산 행렬을 계산한다.
\[\mathbf{C} = \frac{1}{N}\sum^{N-1}_{j=0}(\mathbf{x}_j-\mathbf{m})(\mathbf{x}_j-\mathbf{m})^\top\]고유값 분해를 적용하여 공분산 행렬을 다음처럼 표현할 수 있다.
\[\mathbf{C=UAU^\top}=\sum^{N-1}_{i=1}\lambda_i\mathbf{u}_i\mathbf{u}_i^\top\]이 때, $\lambda_i$는 $\mathbf{C}$의 고유값, $\mathbf{u}_i$는 고유벡터(eigenvectors)이다.
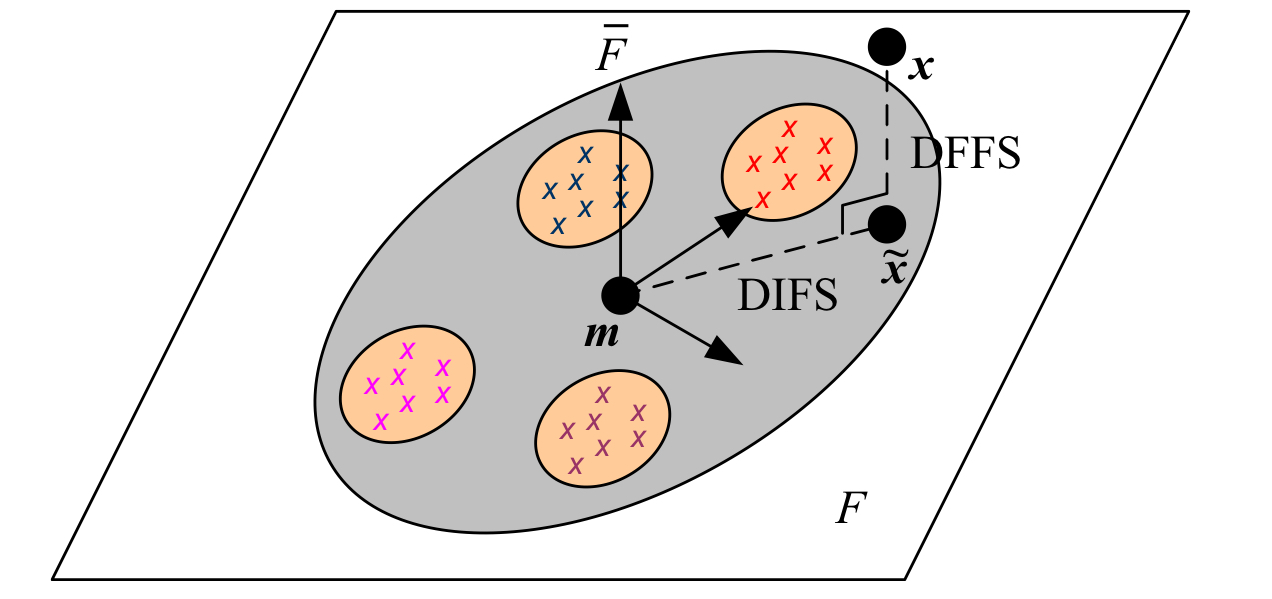
고유값 분해는 두가지 중요한 성질을 가지고 있다. 첫 번째는 새로운 이미지 $\mathbf{x}$의 최적(최근사)의 계수 $a_i$는 다음과 같이 계산할 수 있다는 것이다.
\[a_i = (\mathbf{x-m})\cdot\mathbf{u}_i\]두 번째는 고유값$\lbrace \lambda_i \rbrace$가 내림차 순으로 정렬되어 있다고 가정하면 식 (5.7)의 근사를 어느 지점 $M$에서 잘라(truncate)서 사용하더라도, 그 근사는 $\mathbf{\tilde{x}, x}$ 사이의 오차가 최소가 되는 최적의 근사(best possible approximation)를 제공한다. 얼굴 이미지의 고유 얼굴 분해를 $M$개의 성분까지만 사용하여 잘라내는 것은, 해당 이미지를 선형 부분공간 $F$ 위로 정사영 하는 것과 동일하며, 이 부분공간을 얼굴 공간(face space)라고 부를 수 있다.
왜냐하면 고유벡터(고유얼굴)은 직교하며 단위 노름이고, 정사영된 평면 $\tilde{\mathbf{x}}$로부터 평균 이미지 $\mathbf{m}$으로의 정사영 거리는 다음과 같이 작성 할 수 있다.
\[\text{DIFS}=\lVert \mathbf{\tilde{x}-m}\rVert = \left\lbrack \sum_{i=0}^{M-1}a_i^2 \right\rbrack ^{\frac{1}{2}}\]DIFS는 얼굴 공간의 거리(Distance In Face Space)를 의미한다. 원본 이미지 $\mathbf{x}$의 이미지의 얼굴 공간 $\tilde{\mathbf{x}}$로의 정사영 거리(Distance From Face Space, DFFS)는 픽셀 공간에서 바로 계산할 수 있으며, 이는 특정 이미지가 얼마나 얼굴 같은지를 나타낸다. 또한, 얼굴 공간 안의 각각 다른 두 얼굴은 각각의 고유얼굴 계수차의 노름을 계산함으로써 거리를 거리를 계산할 수 있다.
Manifold learning
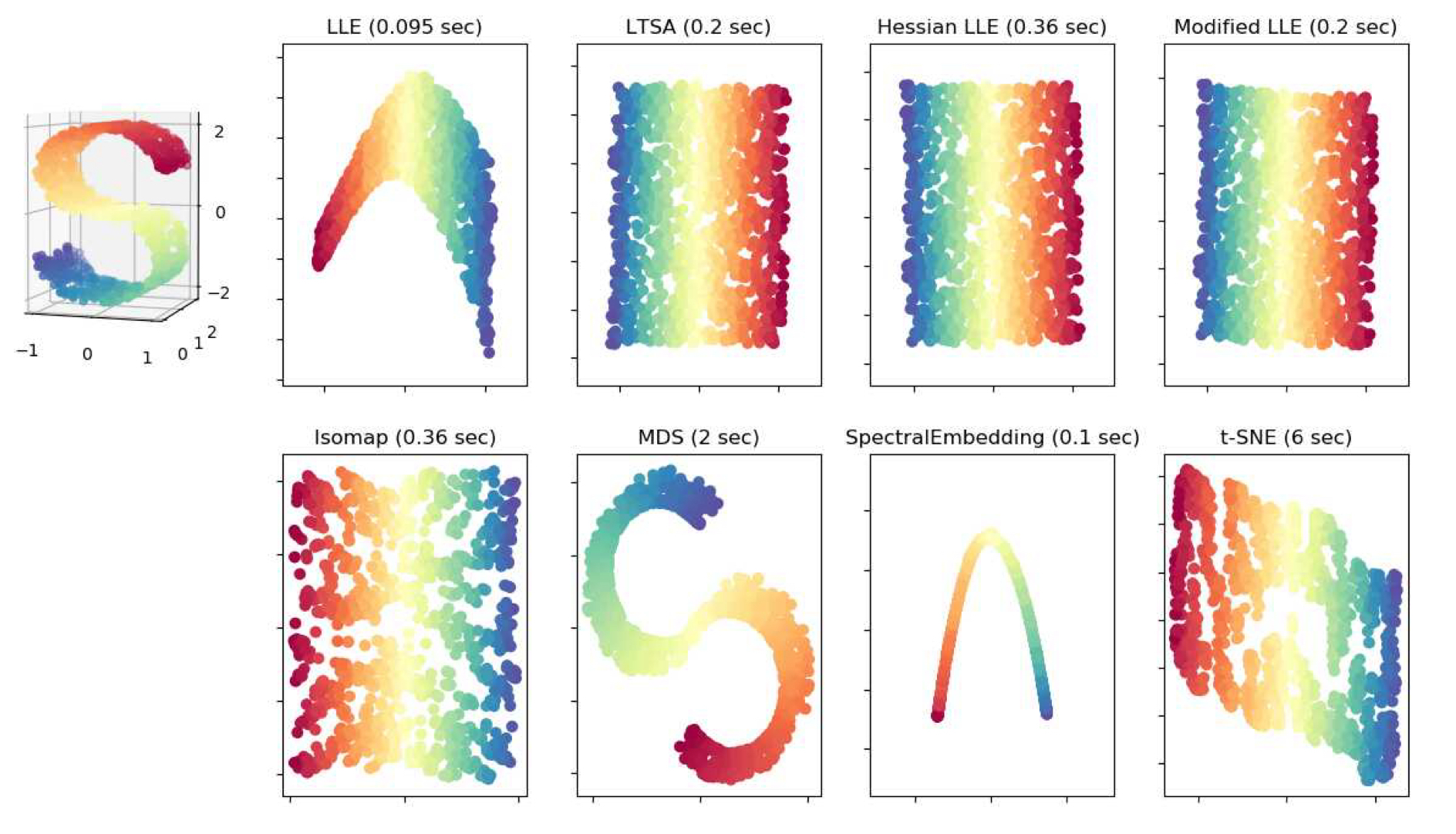
우리가 분석하는 데이터는 전역적으로 선형적인 부분공간에 존재하지 않지만, 더 낮은 차원의 매니폴드 위에는 존재한다. 이러한 경우에는 비선형 차원 축소(non-linear dimensionality reduction) 기법을 사용할 수 있다. 이러한 시스템들은 고차원 공간 내에서 저차원의 매니폴드를 추출하므로 매니폴드 학습 기법(manifold learning techniques)라고도 불린다. 그림 5.17은 3차원 S자형 리본 구조로부터 추출한 2차원 매니폴드 예시이다.
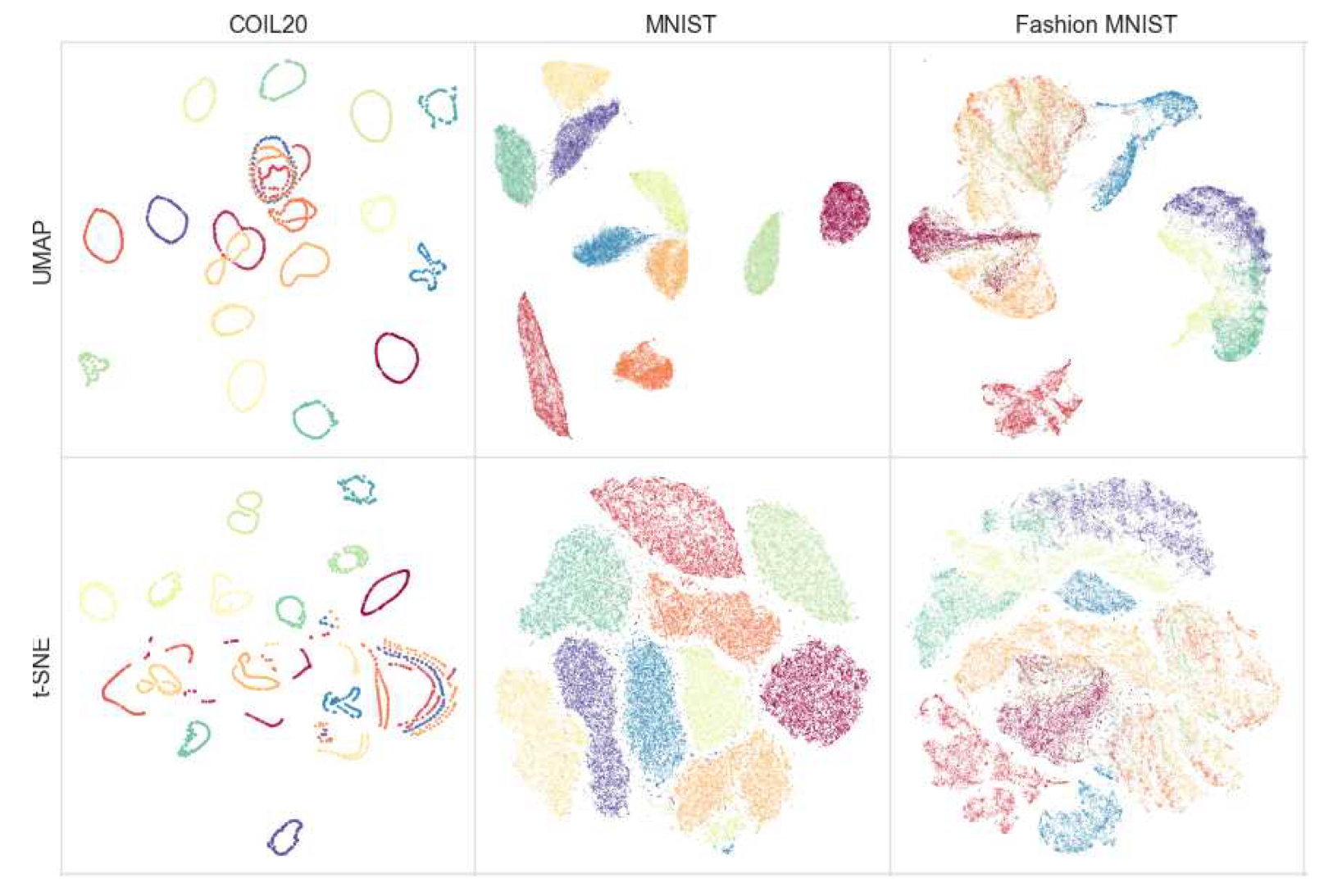
차원 축소는 데이터를 정규화하거나 유사도 탐색을 가속화하는데 유용하다. 뿐만 아니라 매니폴드 학습 알고리즘은 입력 데이터의 분포나 신경망 층의 활성값을 시각화하는 데에도 활용될 수 있다. 그림 5.18은 매니폴드 학습 알고리즘 중 UMAP과 t-SNE를 서로 다른 CV 데이터셋에 적용한 예시를 보여준다.
Semi-supervised learning
ImageNet과 같은 데이터셋은 수십만개의 라벨링된 이미지를 제공하지만 웹에서 수집할 수 있는 대부분의 이미지들은 라벨링이 전혀 되어있지 않는 경우가 많다. 이런 상황에서 학습과 더불어 추후에 올 입력값들의 특성을 제대로 파악해서 더 효과적으로 분류/예측 모델을 만들려면 어떤 방식으로 접근해야 할까?
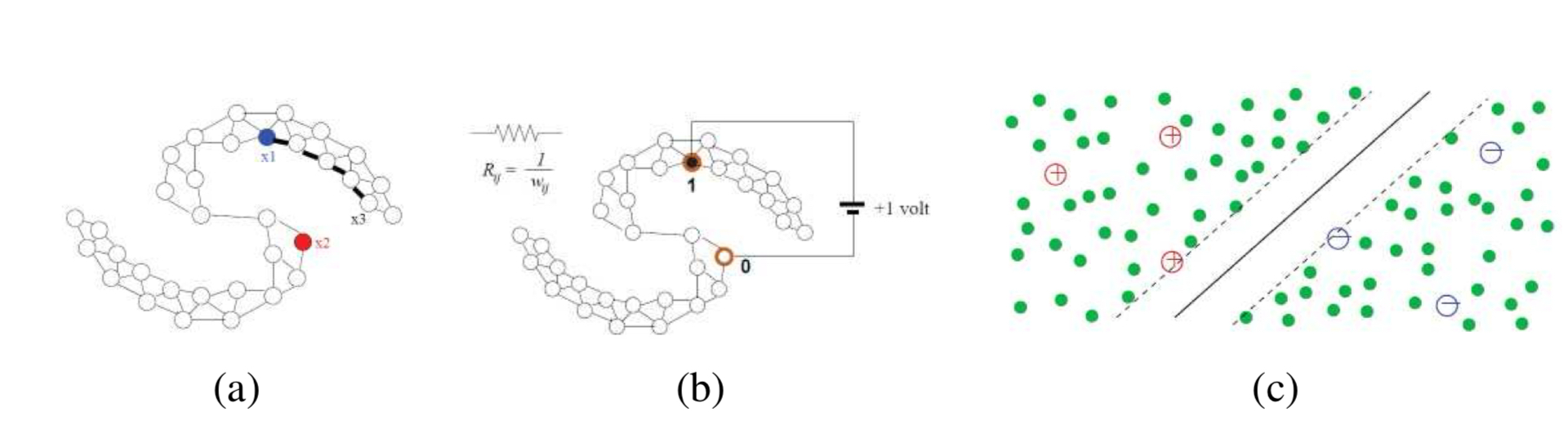
그림 5.19의 다이어그램을 살펴보면, 소수의 표본만이 정확한 클래스로 라벨링 되어있다. 이러한 라벨 정보를 근처의 표본들로 확장함으로써, 모든 데이터에 라벨을 부여하는 수고를 줄일 수 있으며, 동시에 미래 입력값에 대한 결정 경계를 학습할 수 있다.
이런 종류의 학습법을 반지도 학습(semi_supervised learning)이라고 부른다. 반지도 학습은 크게 두가지 갈래로 나뉜다. 첫 번째는 transductive learning이다. transductive learning은 한 배치 안에 라벨링 된 샘플과 그렇지 않은 샘플을 함께 투입해 라벨링 되지 않은 샘플들을 분류하는 것이 목표이다. 두 번째는 inductive learning으로, 이 방식은 모델이 학습 데이터 외의 미래에 주어질 입력값에 대해서도 일반화된 예측을 수행할 수 있도록 훈련하는 것을 목표로 한다. 일반적으로 inductive learning을 주로 사용하며, 자율 주행이나 새로운 컨텐츠에 대한 분류 등의 분야에서 사용된다.
반지도 학습은 약지도 학습(weakly supervised learning)의 한 갈래라고 볼 수 있다. 약지도 학습은 레이블이 없거나, 불완전하거나, 부정확할 수 있는 데이터를 다룬다.
Enjoy Reading This Article?
Here are some more articles you might like to read next: