Figure 5.1 지도학습에서는 입력값과 레이블의 쌍을 이용해, 모델이 주어진 입력으로부터 레이블을 가장 잘 예측할 수 있도록 파라미터를 추정한다.

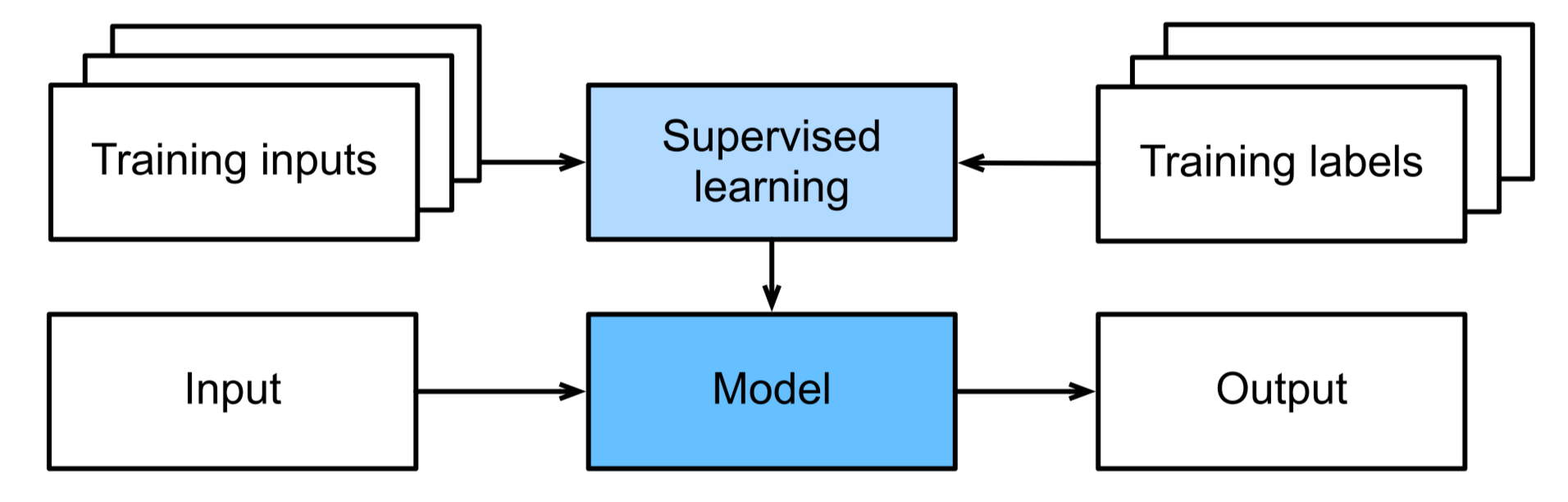
머신 러닝 알고리즘은 크게 입력값과 출력값이 쌍으로 학습 알고리즘에 제공되는 지도학습(Supervised Learning)과 라벨(출력값) 없이 통계적 샘플만을 활용하는 비지도학습(Unsupervised Learning)으로 나뉜다.

위 그림에서 볼 수 있듯이, 지도 학습은 입력 쌍 {$x_i$}와 그에 대응하는 목표 출력값 {$t_i$}를 학습 알고리즘에 입력하는 과정을 포함한다. 이 학습 알고리즘은 모델의 예측값과 목표 출력값 사이의 일치하는 정도를 최대화 하기 위해 모델의 파라미터를 조정한다. 이때, 출력은 클래스 집합 {$C_k$}로부터 나오는 이산적인 레이블일 수도 있고, 혹은 연속적이며 잠재적으로 벡터 값을 가질 수도 있다. 이러한 출력 유형의 구분을 명확히 하기 위해 $y_i$로 나타낸다. 이산적인 레이블을 예측하는 경우는 클래스의 소속 여부를 예측하려는 것이므로 분류(Classification)라고 하며, 연속적인 값을 예측하는 경우는 전통적으로 데이터에 추세를 맞추는 문제로 간주되어 회귀(Regression)라고 불린다.

모델의 학습 단계(training phase)이후에는, 이전까지 학습되지 않았던 입력값에 대한 예측을 수행하게 되고, 이 단계를 테스트 단계(test phase)라고 한다.

머신 러닝에서는 일반적으로 입력에 대한 실제 확률 분포와 그에 대응하는 출력에 대한 결합 분포 데이터에 접근할 수 없기에 실제 세계의 분포를 대신하여 훈련 데이터의 분포를 일반적으로 사용한다. 이러한 근사는 경험적 위험 최소화(empirical risk minimization)이라고 알려져 있으며, 기대 위험을 다음과 같이 추정할 수 있다.

\[E_{\text{Risk}}(\mathbf{w}) = \frac{1}{N}\sum L(y_i,f(x_i;\mathbf{w}))\]

손실 함수 $L$은 입력 $x_i$와 모델 파라미터 $\mathbf{w}$에 대해 예측 함수 $f(x_i; \mathbf{w})$가 생성한 출력이 실제 목표값 $y_i$와 얼마나 차이 나는지를 나타내는 “비용”을 측정한다.

Data preprocessing

중심화(Centering) : 각 벡터에서 평균값을 빼는 것
표준화(Standardizing) : 각 성분을 다시 스케일링하여 그 분산이 1(Unit-Variance)이 되게 하는 것
Whitening : 입력값의 공분산 행렬을 계산하고, 특이값 분해(SVD)한 후, 좌표계를 회전시켜 최종 차원들이 서로 상관이 없고 분산이 1이 되도록 하는 것. 컴퓨팅 비용이 많이 요구되므로 입력값이 저차원일때 효과적이다.

Nearest Neighbors

Nearest neighbors는 매우 단순한 비모수(non-parametric) 기법이다. 조금 더 상세하게 설명하자면, 기저 분포(underlying distribution)에 대해 소수의 파라미터를 가진 해석적(analytic) 형태를 사용하지 않는 기법이다. 대신, 모든 훈련 데이터를 그대로 유지하며, 평가 시점에는 ‘가장 가까운’ $k$개의 이웃을 찾아 평균 내어 출력을 생성한다.

Figure 5.2 Nearest neighbor classification. 별이 어떤 클래스에 속하는지 결정하기 위해 k개의 근접한 이웃들을 찾고, 그 중에서 가장 많은 클래스를 선택한다. 그림은 k=1, 9, 25 일때의 결과를 나타낸다.

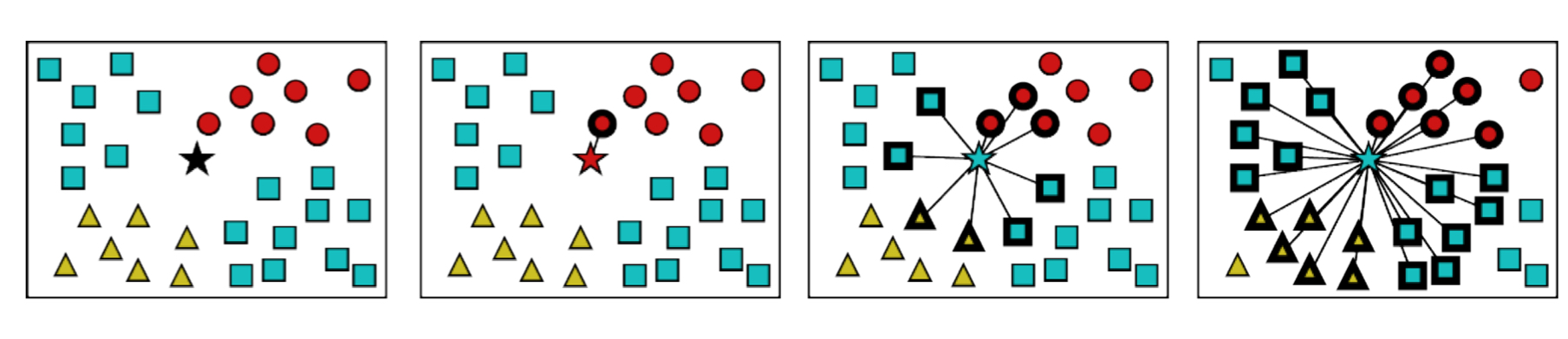
그림 5.2는 $k=1$부터 $k=25$까지의 변화를 보여주는 그림이다. $k$값의 변화가 곧 최종 분류 레이블에 영향을 영향을 미침을 알 수 있다.

Figure 5.3 경계가 불분명한 데이터에 대해 너무 작은 k값을 선택하면, 결정 평면의 비균질성을 불러일으킨다. 반면, 너무 큰 값은 작은 영역이 찌끄러지거나 사라지게 만든다.

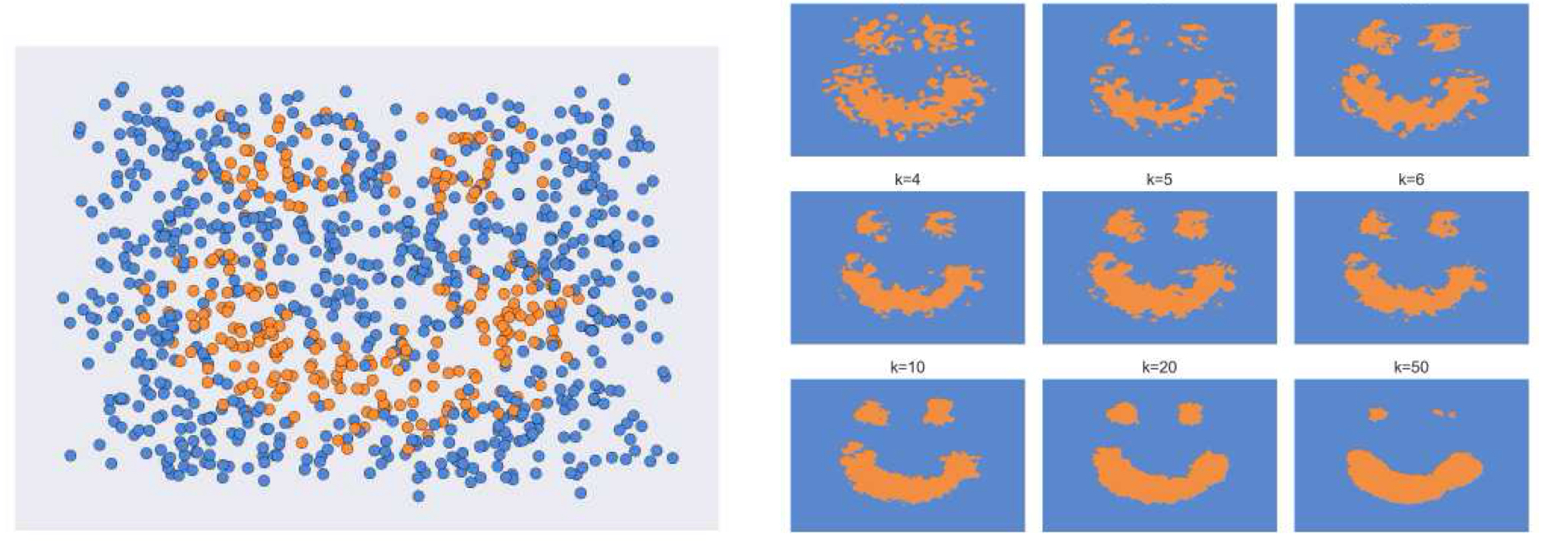
그림 5.3은 $k$의 변화가 미치는 다른 영향을 보여준다. 그림의 좌측은 샘플의 초깃값을 보여주는데, 보면 알 수 있듯이 파란색과 주황색이 구분없이 굉장히 뒤섞여있음을 알 수 있다. 그림의 우측은 1 부터 50까지의 $k$ 값에 따른 $k$-NN 분류기의 결정 경계(decision boundaries)을 보여준다.$k$ 값이 너무 작으면, 분류기는 훈련 데이터에 오버피팅되어 예측 결과가 불안정하고 무작위적인 경향을 보인다. 반대로, $k$값이 커지면, 분류 경계가 지나치게 부드러워지며 소규모 영역이 축소되는 등 데이터의 언더피팅 문제가 발생한다. 따라서, $k$는 분류기의 성능을 좌우하는 중요한 하이퍼파라미터로, 적절한 값을 선택하는 것이 핵심임을 알 수 있다.

Bayesian Classification

Figure 5.4 두 개의 클래스 조건부 확률 밀도 함수와, 이에 대응하는 후험 클래스 확률를 함께 나타낸 예를 생각해보자. 이 후험 확률은 베이즈 정리를 이용해 계산할 수 있으며, 이는 두 곡선의 합으로 나눈 값을 의미한다. 녹색 수직선은 오분류율을 최소화하는 최적의 결정 경계선이다.

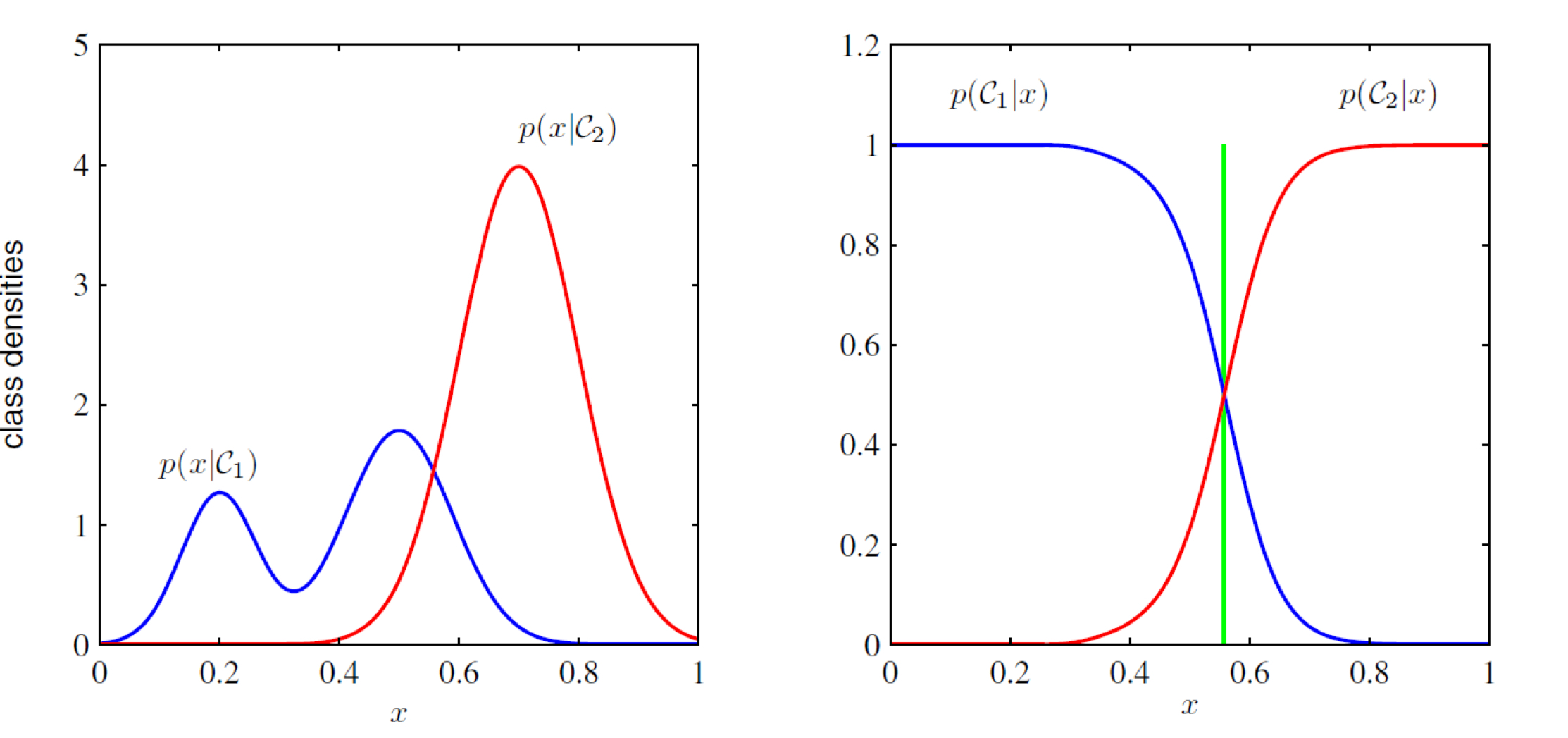
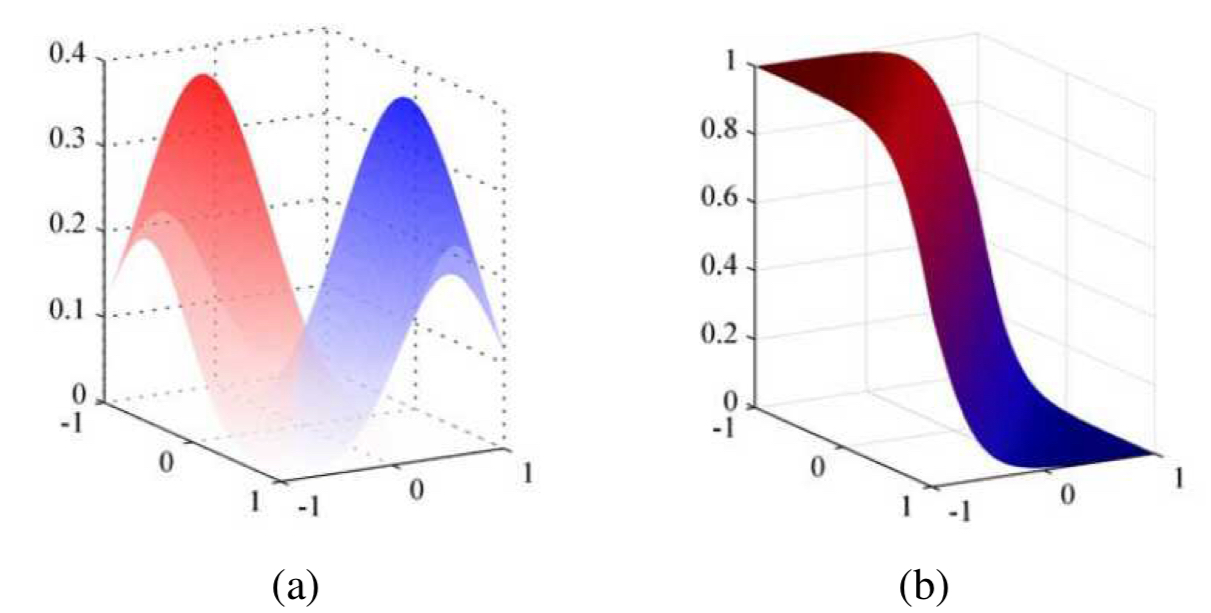
일부 단순한 머신러닝 문제에서는, 각 클래스에 대한 특성 벡터의 조건부 확률 분포 $p(\mathbf{x} \vert C_k)$뿐만 아니라, 클래스의 사전 우도 $p(C_k)$ 역시 결정할 수 있다. Bayes’ rule에 의해 특성 벡터 $\mathbf{x}$가 주어졌을 때 클래스 $C_k$의 우도(그림 5.4)는 다음과 같이 주어진다.

\[\begin{align} p_k = p(C_k\vert \mathbf{x}) &= \frac{p(\mathbf{x}\vert C_k)p(C_k)}{\sum_jp(x\vert C_j)p(C_j)} \tag{5.1} \\ &= \frac{\exp l_k}{\sum_j \exp l_j} \tag{5.2} \end{align}\]

Remark. $P(A\vert B)$ : 조건부 확률, B가 주어졌을 때 A가 일어날 확률

이 때, $\frac{\exp l_k}{\sum_j \exp l_j}$는 정규화된 지수 함수(normalized exponential) 또는 소프트 맥스 함수(softmax function)라고 부른다. $l_k$에 대해

\[l_k=\log p(\mathbf{x}\vert C_k)+ \log p(C_k)\]

는 샘플 $\mathbf{x}$가 클래스 $C_k$에 속할 때의 로그-우도(log-likelihood)를 의미한다.

소프트 맥스 함수는 벡터에서 벡터로의 함수 형태로 나타내기도 하며, 이때는 다음과 같이 표기한다.

\[\mathbf{P}=\text{softmax}(\mathbf{l})\]

소프트 맥스 함수는 최댓값 지시 함수(maximum indicator function)의 부드러운 형태로 볼 수 있다. 이 함수는 $l_k$가 다른 값들에 비해 큰 값일 때, 해당 $l_k$에 대해 1을 반환한다.

특성 벡터 $\mathbf{x}$가 주어졌을 때 클래스 $C_k$의 우도를 결정할 때 사용되는 공식(5.1)을 이용하는 방법을 베이즈 분류(Bayesian classification)라고 한다. 왜냐하면 이 방법은 베이즈 정리를 이용해 조건부 특성 우도 $p(\mathbf{x} \vert C_k)$와 클래스에 대한 사전 분포 $p(C_k)$를 결합함으로써, 후험(posterior) 클래스의 확률을 결정하기 때문이다.

또한, 다음과 같이 특성 벡터의 각 구성 요소들이 독립적으로 생성된다고 가정하는 경우에는 나이브 베이스 분류(_naïve Bayes classifier)라고 한다.

\[p(\mathbf{x}\vert C_k) = \prod_i p(x_i \vert C_k)\]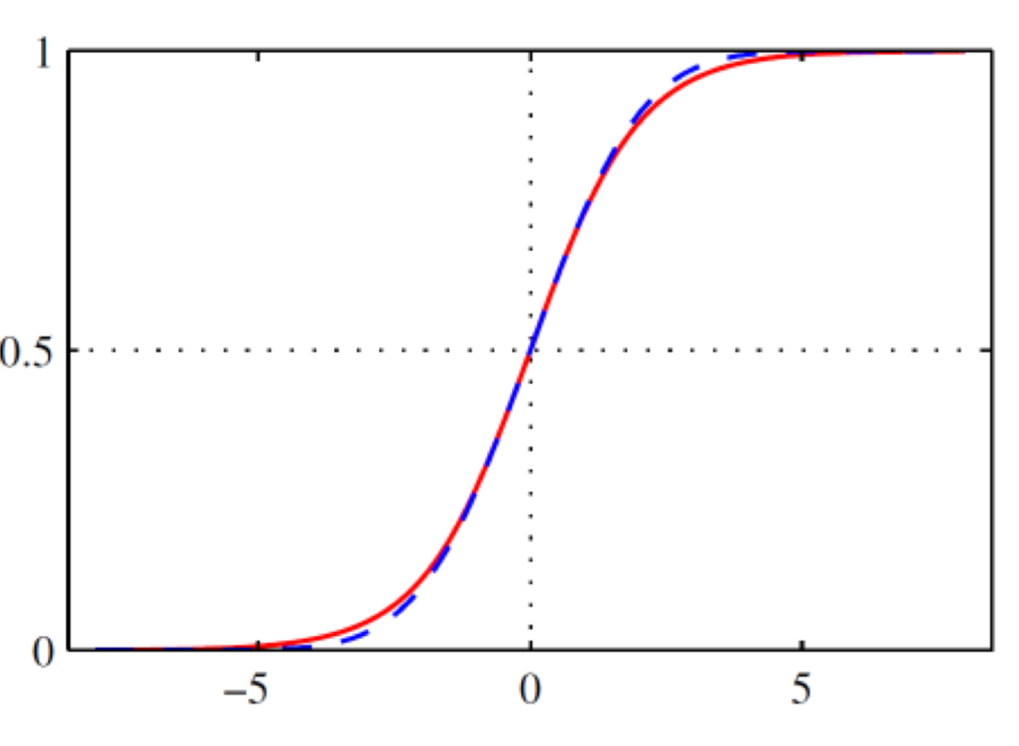

Figure 5.5 붉은색은 로지스틱 시그모이드 함수, 파란색은 수정된 오차함수

이진 분류 문제에서는 공식(5.2)를 다음과 같이 쓸 수 있다.

\[p(C_0 \vert \mathbf{x}) = \frac{1}{1+\exp(-l)}=\sigma(l)\]

이때 $l=l_0-l_1$은 두 클래스 로그-우도의 차이이며 로그 오즈(log odds) 또는 로짓(logit)라고 한다.

$\sigma(l)$함수는 로지스틱 시그모이드 함수(logistic sigmoid function) 또는 로지스틱 함수라고 부르며, 시그모이드는 S자 커브를 의미한다.

LDA(Linear Discriminant Analysis)와 QDA(Quadratic Discriminant Analysis)

LDA

Figure 5.6 두 개의 유일하게 분포된 가우스 클래스의 로지스틱 회귀. (a) 두 개의 가우스 분포가 파랑/빨강으로 표현되어있다. (b) 후험 확률은 함수의 높이와 붉은색 잉크의 비율로 표현되어있다.

소프트맥스 함수와 시그모이드 함수에 기반한 확률적 생성 분류 모델은 모든 로그-우도 집합에 적용할 수 있지만, 분포가 다변량 가우스 형태를 띌 경우 수식이 훨씬 간단해진다. 공분산 행렬 $\Sigma$가 동일한 가우스 분포에 대해서는 다음 수식을 적용할 수 있다.

\[p(\mathbf{x}\vert C_k)=\frac{1}{(2\pi)^{D/2}}\frac{1}{\lVert\Sigma\rVert^{1/2}}\exp \left\lbrace -\frac{1}{2}(\mathbf{x}-\mu_k)^\top\Sigma^{-1}(\mathbf{x}-\mu_k)\right\rbrace\]

이진 분류 문제에서는 다음과 같이 쓸 수 있다.

\[\begin{align} &p(C_0 \vert \mathbf{x}) = \sigma(\mathbf{w^\top x}+b) \tag{5.3}\\ &\mathbf{w}=\Sigma^{-1}(\mu_0-\mu_1), \tag{5.4} \\ &b = \frac{1}{2}\mu_0^\top\Sigma^{-1}\mu_0 +\frac{1}{2}\mu_1^\top\Sigma^{-1}\mu_1 + \log\frac{p(C_0)}{p(C_1)} \end{align}\]

수식 5.3은 비생성형 기반 분류에서 사용되는 로지스틱 회귀(logistic regression)이다. 로지스틱 회귀 라고 불리는 이유는 선형 회귀 식(logit function)

\[l(\mathbf{x}) = \mathbf{w^\top x} + b \tag{5.5}\]

의 출력을 로지스틱 함수에 통과시켜 클래스 확률을 얻기 때문이다. 이때, 선형 회귀 식 (5.4)에서 $\mathbf{w}$는 가중치 벡터를, $b$는 편향을 의미하며 이 둘은 분류 경계를 결정한다.

가중치 벡터 방향(5.4)은 좌표계를 공분산 행렬의 역행렬 $\Sigma^{-1}$에 의해 회전한 뒤, 두 분포의 평균 벡터를 연결하는 방향과 일치함에 주목하자. 또한, 편향항은 평균 제곱 모먼트들과 클래스 사전 확률의 로그 비율 $\log(p(C_0)/p(C_1))$에 비례한다.

QDA

Figure 5.7 QDA. 클래스 공분산이 다를 때, 가우스 분포간의 결정 평면은 이차곡선평면의 형태를 띈다.

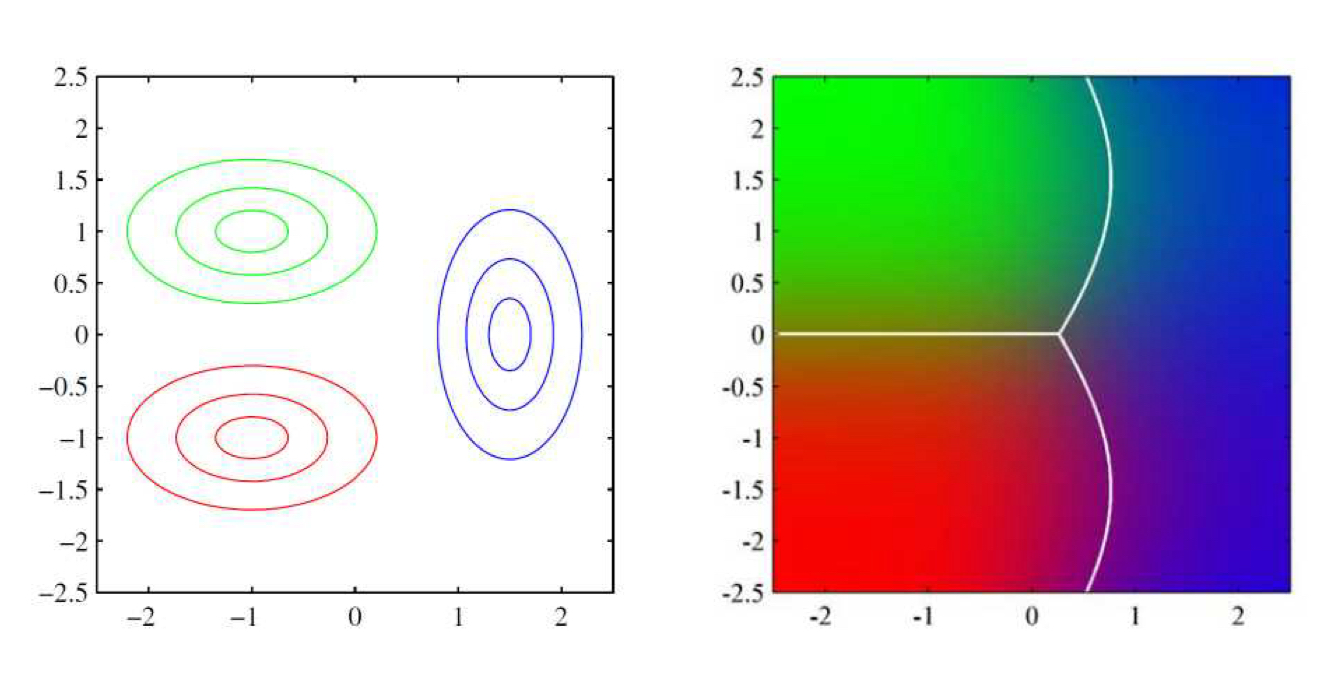
클래스가 2개 이상인 경우에 소프트 맥스 함수(5.2)는 선형 로그 우도에 다음과 같이 적용될 수 있다.

\[\begin{align} &l_k(\mathbf{x})=\mathbf{w}_k^\top\mathbf{x}+b_k \\ &w_k=\Sigma^{-1}\mu_k\\ &b_k = -\frac{1}{2}\mu_k^\top\Sigma^{-1}\mu_k + \log p(C_k) \end{align}\]

분류가 한 클래스에서 다른 클래스로 전환되는 결정 경계가 선형이기 때문에 결정 기준을 다음과 같이 표현할 수 있다.

\[\mathbf{w}_k \mathbf{x} + b_k > \mathbf{w}_l\mathbf{x}+b_l\]

이러한 기준을 사용하여 데이터를 분류하는 기법은 선형 판별 분석(linear discriminant analysis, LDA)라고 한다.

지금까지 살펴본 경우들은 모두 클래스의 공분산 행렬 $\Sigma_k$가 유일한 경우이며, 그렇지 않을 경우 결정 평면은 선형을 유지하지 않으며 quadratic함을 (그림5.7)을 통해 보인다. 이런 이차 결정 평면을 사용하는 기법은 이차 판별 분석(quadratic discriminant analysis, QDA)라고 한다.

Logistic Regression

클래스 분포 문제를 해결하는 가장 쉬운 방법 중 하나는 로지스틱 회귀(logistic regression)이다. 베이시안 분류에서 사용되었던 것과 동일하게 가중치 벡터에 선형 투영을 적용하는 개념을 사용한다.

\[l_i = \mathbf{w\cdot x}_i + b\]

이 선형 투영 결과를 로지스틱 함수에 적용하면

\[p_i=p(C_0\vert \mathbf{x}_i)=\sigma(l_i)=\sigma(\mathbf{w^\top x}_i+b) \tag{5.6}\]

를 사용하여 이진 클래스 확률을 얻을 수 있다.

로지스틱 함수는 미지의 변수들에 대한 사전 확률 분포를 따로 구성하거나 가정하지 않기 때문에 판별(discriminative) 모델의 간단한 예시 중 하나라고 볼 수 있다.

따라서 클래스 평균과 공분산을 추정하여 분석할 수 없기 때문에 가중치 $\mathbf{w}$와 편향 $b$를 구하는 새로운 방법이 필요한데, 정답 클래스의 로그 후험 확률을 최대화 함으로써 구할 수 있다.

이진 분류 문제에서, 각 훈련 샘플 $x_i$에 대한 클래스 레이블이 $t_i \in \lbrace 0,1 \rbrace$라고 하자. 또한, $p_i = p(C_0\vert \mathbf{x})$는 주어진 가중치와 편향 $(\mathbf{w}, b)$에 대해 로지스틱 함수(5.6)에 따라 계산된 클래스 $C_0$의 추정 확률이라고 하자. 이때, 로그 우도의 음수를 최소화 하는 방법으로 추정된 올바른 라벨에 대한 우도를 최대화 할 수 있으며, 이를 크로스-엔트로피 손실(cross-entropy loss) 또는 오류 함수(error function)라고 한다. 이는 모델이 정답 클래스에 대해 높은 확률을 출력하도록 유도하는 손실 함수로, 확률적 해석과 최적화 모두에서 직관적이며 널리 사용된다.

\[E_{CE}(\mathbf{w},b) = - \sum_i \lbrace t_i\log p_i+(1-t_i)\log(1-p_i)\rbrace\]

라벨이 $t_i=0$일 경우, 모델이 예측한 확률 $p_i = p(C_0\vert \mathbf{x}_i)$가 가장 높아야 하며, 반대로, $t_i=1$일 경우에는 이 값이 낮게 나와야 한다는 점에 주목하자.

이 수식은 클래스 마다 수행된 선형 회귀 결과에 정규화된 지수 함수를 적용하여 후험 확률을 정의함으로써, 다중 클래스 손실(multi-class loss)로 확장될 수 있다.

\[p_{ik} = p(C_k\vert \mathbf{x}_i) = \frac{\exp l_{ik}}{\sum_j \exp l_{ij}} = \frac{1}{Z_i}\exp l_{ik}\]

이때, $l_{ik} = \mathbf{w}_k^\top\mathbf{x}_i + b_k$이다.

수식 $Z_i = \sum_j \exp l_{ij}$는 정규화 상수(partition function)로 소프트맥스 함수의 분모에 해당하며 확률 분포로 정규화하는 역할을 한다. 위 형태에서 일부 전개 과정을 거치면 이에 대응하는 다중 클래스 크로스 엔트로피 손실 함수(multi-class cross-entropy loss)를 다음과 같이 구할 수 있다.

\[E_{MCCE}(\lbrace\mathbf{w}_k,b_k\rbrace) = - \sum_i\sum_k\tilde{t}_{ik}\log{p_{ik}}\]

여기서 $\tilde{t}_{ik}$는 원-핫 인코딩을 의미하며, 샘플 $i$가 클래스 $k$에 속할 경우 1, 그렇지 않으면 0이 된다. 클래스 레이블을 원-핫 벡터 대신 정수형 값 $t_i \in \lbrace 0,1, \ldots, K-1\rbrace$로 표현하면 손실 함수는 다음과 같이 더욱 간결하게 쓸 수 있다.

\[E(\lbrace \mathbf{w}_k, b_k) = -\sum_i \log{p_{it_i}}\]

또한 소프트맥스 확률 정의를 손실 함수에 직접 대입하면, 각 샘플 $i$에 대해 다음과 같이 정리할 수 있다.

\[E(\lbrace \mathbf{w}_k, b_k) = -\sum_i(\log Z_i - l_{it_i})\]

최적의 가중치와 편향값을 결정하기 위해서 경사 하강법(gradient descent)를 사용할 수 있다.

\[\mathbf{w \leftarrow w -H^{-1}}\nabla E(\mathbf{w})\]

이 때, $\nabla E$는 손실함수 $E$를 가중치 변수 $\mathbf{w}$에 대해 편미분한 경사(gradient)를 의미하고, $\mathbf{H}$는 이차 편미분으로 구성된 헤세 행렬(Hessian matrix, 곡률 정보를 담고 있다.)이다. 크로스-엔트로피 함수는 미지의 가중치 변수에 비선형이기 때문에, 반복해서 위 수식을 전개하면 최적의 해를 찾을 수 있다.

이 방법은 손실 함수의 이차 근사를 통해 반복적으로 가중 최소제곱(weighted least squares) 문제를 푸는 방식이며, 각 반복 단계에서 헤세 행렬이 갱신된다는 점에서 반복 가중 최소제곱법(iteratively reweighted least squares, IRLS)이라고 불린다.

많은 비선형 최적화 문제들은 다수의 국소 한계점(local minima)을 가지지만, 크로스-엔트로피 함수는 그렇지 않기 때문에, 유일 해에 도달할 수 있음을 보장받는다.

Support vector machines

Figure 5.8 (a) SVM이 근접한 훈련 샘플(서포트 벡터)에 대한 마진을 최대화하는 선형 결정 평면(하이퍼플레인)을 찾는다. (b) 두 클래스에 적용된 가우스 커널 SVM. x는 훈련 샘플을, 원이 쳐진 샘플들은 서포트 벡터를 나타낸다. 검은 선들은 커널 회귀 함수의 등고선을 나타내며, 그 중 파란색과 빨간색 서포트 벡터를 지나는 선들은 ±1 마진 경계이고, 이들 사이의 짙은 검정색 선이 실제 결정 경계(decision surface)이다.

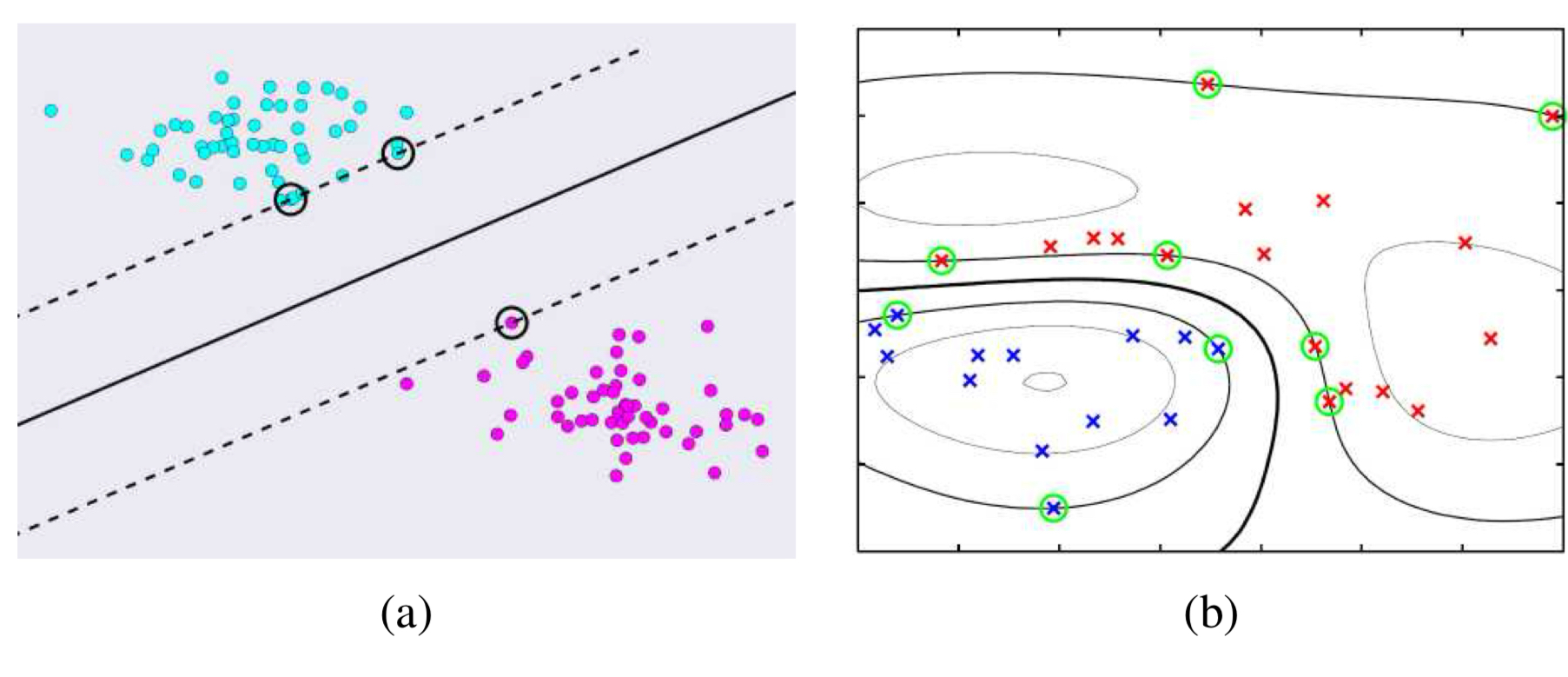
가끔 로지스틱 회귀를 적용하다 보면 피처 공간 사이의 갭(gap)으로 인해 단일한 최적의 결정 평면을 정의하지 못하는 경우가 있다.

그림 5.11(a)는 푸른 점(클래스)와 붉은 점(클래스)를 완벽하게 분할하는 무수히 많은 선들이 존재한다. 이 무수히 많은 결정선들이 학습 데이터를 완벽히 분류하므로 오류는 없지만, 역설적으로 어떤 결정 경계가 가장 좋은지 선택하는 방법은 무엇일까?

위 문제에 대한 정답은 최대 마진 분류기(maximum margin classifiers)를 사용하는 것이다. 그림(a)에서 점선은 둑 개의 평행한 결정 경계를 나타내며, 이들은 서로 간의 수직 거리가 가장 큰 최대 마진을 가진다. 이때, 점선으로 결정된 평면을 반으로 가르는 직선이 최대 마진 분류기라고 할 수 있다.

최대 마진 분류기를 정의하기 위해서 모든 회귀 값 $l_i=\mathbf{w \cdot x}_i+b$의 절댓값이 최소 1 이상이고 올바른 부호를 가지는 가중치-편향 쌍($\mathbf{w},b$)를 찾아야 한다.

\[\hat{t}_i = 2t_i - 1, \quad \hat{t}_i \in \lbrace -1, 1 \rbrace\]

위 $\hat{t}_i$를 부호 클래스 레이블(signed class label)이라고 하면 부등식(inequality condition)을 다음과 같이 쓸 수 있다.

\[\hat{t}_i(\mathbf{w\cdot x}_i+b) \ge 1\]

이 마진을 최대화 하기 위해서 위 부등식을 만족하는 가장 작은 노름 가중치 벡터 $\mathbf{w}$를 찾아야 한다.

\[\arg\min_{\mathbf{w},b}\lVert \mathbf{w} \rVert^2\]

지금까지 기술한 문제를 해결하는 방법은 고전적인 이차 계획법(quadratic programming problem)이 문제로, 라그랑주 승수법(Lagrange multipliers)을 이용해 풀 수 있다.

부등식 제약 조건은 정확하게 점선 위에서 성립하며, 이때는 등식 조건 $l_i=\mathbf{wx}_i +b = \pm 1$로 바뀐다. 이때, 이 점선에 닿아 있는 동그라미 친 데이터 포인트들을 서포트 벡터(support vector)라고 부른다. 간단한 선형 분류에서 서포트벡터는 결정 평면을 측정하도록 도와주는 것 외에는 아무런 이점이 없다. 그러나, 커널 회귀를 적용할 때에는 적은 수의 서포트 벡터만으로도 큰 이점을 가져갈 수 있다.

만약 두 클래스가 선형으로 분류할 수 없다면 그림(b)처럼 샘플들을 분류하기 위해 복잡하게 휘어진 평면이 필요하다. 이런 경우에 선형 회귀가 아닌 커널 회귀(kernel regression)을 적용할 수 있다. 커널회귀는 선형 회귀와는 다르게 가중치 벡터를 피처 벡터에 곱하는 대신 학습 데이터 포인트 $\mathbf{x}_k$를 중심으로 정의된 커널 함수($K$)의 값들과 가중치를 곱해 사용하는 방식으로 바뀐다.

\[l_i = f(\mathbf{x}_i;\mathbf{w},b) = \sum_k w_k\phi(\lVert \mathbf{x}_i - \mathbf{x}_k \rVert) + b\]

모든 학습 데이터 포인트의 합 대신 최대 마진 분류기를 학습하고 나면, 전체 데이터 중 일부 서포트 벡터만 남겨도 충분하다(그림(b)의 동그라미 친 x 점들). 그림에서 진한 검정색 선으로 그려진 결정 경계는 붉은색과 푸른색 클래스 샘플을 원만하게 분리하고 있다. 하지만 커널 회귀의 다른 경우와 마찬가지로, 커널의 너비는 여전히 하이퍼 파라미터로 남아 있기 때문에, 이를 적절히 설정하여 오버/언더피팅을 방지해야 함에 유의하자.

Hinge Loss

Figure 5.9 뒤섞인 훈련 샘플에 대한 SVM. (a) 녹색 원으로 표시된 데이터 포인트는 y=1 마진 경계를 침범하고 있으며, 슬랙 변수 1-y 만큼의 패널티를 갖는다. 이 값은 마진 위반의 정도를 수치적으로 나타내며 슬랙변수가 0보다 크면 해당 샘플은 마진 안쪽에 있음을 의미한다. (b) SVM에서 힌지 로스가 사용된 부분은 파란색으로, 로지스틱 회귀 손실 함수가 사용된 부분은 붉은색으로, 오분류 오류의 발생은 검정색으로, squared error는 녹색으로 표시되어있다.

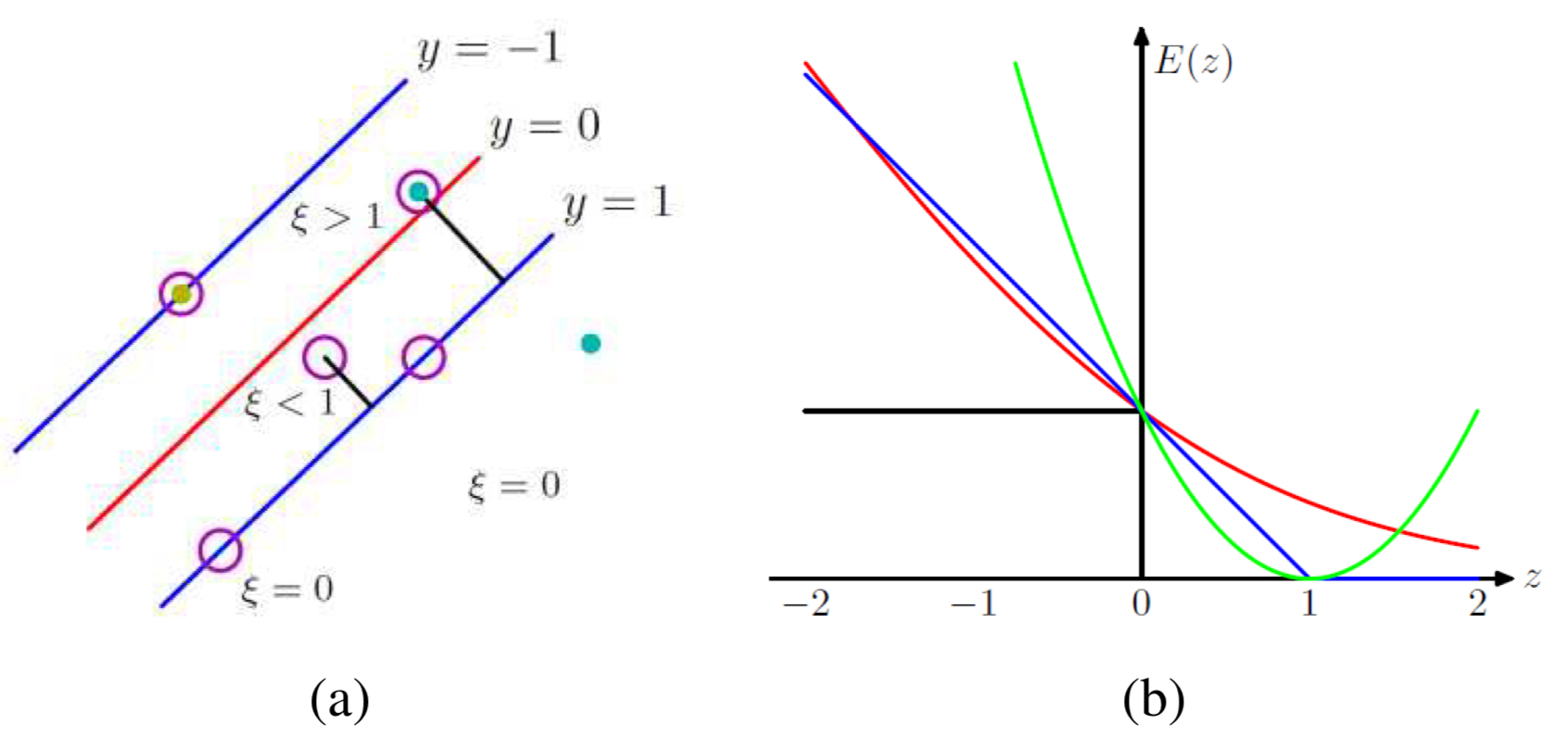
서포트 벡터 머신은 클래스 분포가 뒤섞여 있을 때도 적용할 수 있다. 이번에는 부등식을 힌지 로스 페널티(Hinge Loss Penalty)로 대체해보자.

\[E_{\text{HL}}(l_i,\hat{t}_i)=[1-\hat{t}_il_i]_+\]

여기서 $[\cdot]_{+}$ 은 양의 부분, 즉, $[x]_{+}=\max(0,x)$를 의미한다.

슬랙 변수 $\xi_i$는 각 데이터 포인트가 마진을 얼마나 위반했는지를 나타낸다.

$\xi_i=0$ : 마진 바깥에 제대로 분류됨 $0<\xi_i<1$ : 마진 내부에 있지만 여전히 올바르게 분류됨 $\xi_i > 1$ : 오분류(misclassified)된 샘플

그림 5.9(b)에서 파란색 선으로 표현된 힌지 로스 패널티는 SVM에서 언급했던 부등식을 충족하면 0이 되며, 제약 조건을 위반한 정도에 따라 손실이 선형적으로 커진다는 의미이다.

최적의 가중치 값$(\mathbf{w},b)$를 찾기 위해선 정규화된 힌지 로스 값의 합을 최소화해야한다.

\[E_{\text{SV}}(\mathbf{w},b) = \sum_i E_{\text{HL}}(l_i(\mathbf{x}_i;\mathbf{w},b),\hat{t}_i) + \lambda \lVert \mathbf{w} \rVert^2\]

그림 (b)에서는 힌지 로스와 로지스틱 회귀에서 사용하는 크로스 엔트로피 로스를 비교하고 있다. 힌지 로스는 $\lvert l_i \rvert > 1$인 경우, 즉, 마진을 충분히 만족하는 샘플에 대해서는 손실을 부과하지 않지만, 크로스 엔트로피 손실은 정확히 분류된 경우에도 $\lvert l_i \rvert$가 클수록 더 좋은 것으로 간주한다.

	Hinge Loss (SVM)	Cross-Entropy Loss (Logistic Regression)
마진 외 샘플에 대한 손실	없음 ($l_i > 1$이면 손실 0)	항상 존재하지만 로짓이 커질수록 감소
분류 기준	$\hat{t}_i l_i > 1$	정답 클래스에 해당하는 $l_i$가 클수록 손실 감소
목적	마진 극대화	정답 클래스 확률 극대화
손실 증가 방식	선형 증가 $(\text{max}(0, 1 - \hat{t}_i l_i))$	로그 기반 완만한 증가

실제 문제에서는 SVM의 힌지 로스가 분류에만 집중하는 한편, 로지스틱 회귀는 확률 예측까지 고려하는 모델이다. 따라서 예측 확률이 필요한 문제와 명확한 결정 경계가 필요한 경우로 구분하여 SVM과 로지스틱 회귀를 적합하게 사용할 수 있다.

Decision trees and forests

Figure 5.10

의사결정 트리(decision trees)는 다음 요소로 어떤 것을 선택할 지 결정하기 전에 각각의 피처 요소를 먼저 탐색하는 간단한 작업을 단계별로 수행한다. 의사결정 트리는 통계적 머신러닝에서 오랜 기간 활용되어 왔지만, 이보다 더 강력한 형태인 Decision Forest는 최근 10여년 사이에 들어서야 비전 분야에서 활용되기 시작했다. 서포트 벡터 머신과 마찬가지로 의사결정 트리는 데이터를 분류할 때 해당 데이터의 확률 분포를 따로 구성하지 않기에 판별 분류기(discriminative classifiers)이다.

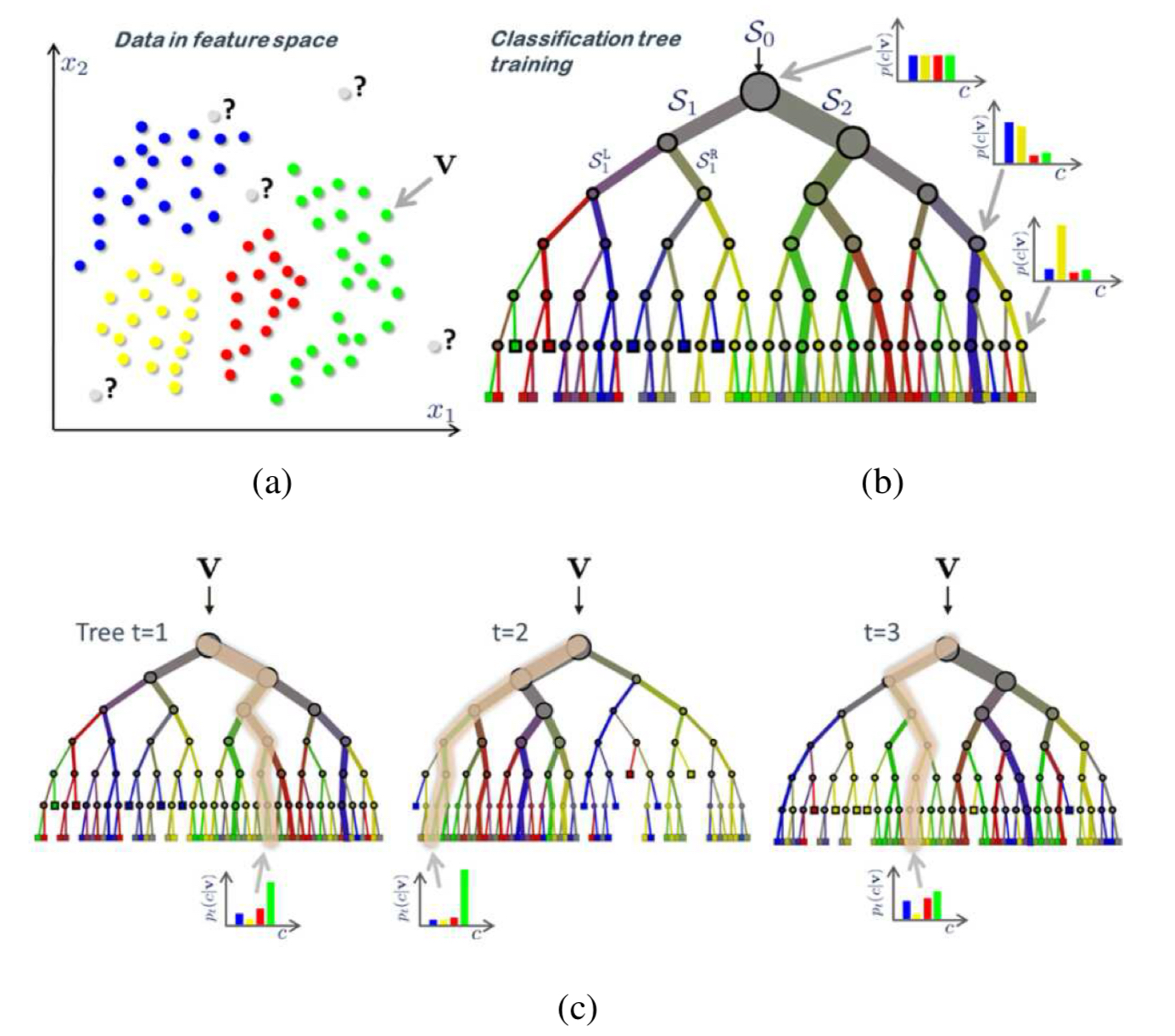
그림 5.10은 의사결정 트리와 랜덤 포래스트의 기본적인 개념이 그려져있다. 이미지의 예시는 각각 다른 네 개의 클래스의 훈련 샘플로 구성되어 있으며, 의사결정 트리(b)는 위에서 아래로 구성되며, 각 노드에서 해당 노드에 도달한 훈련 샘플들을 더 구체적이고 더 낮은 엔트로피의 분포로 나누는 결정을 선택한다. 각 링크의 두께는 해당 경로를 따라 분류된 샘플 수를 나타내고, 링크의 색상은 그 경로를 따라 흐르는 클래스 색상의 혼합으로 표현된다. 색상 히스토그램은 내부 노드의 클래스 분포를 보여준다.

랜덤 포레스트(c)는 각기 다른 결정을 내리는 다수의 의사결정 트리의 집합으로 이루어진다. 테스트 시에 새로운 샘플은 랜덤 포레스트에 속한 각각의 트리들에 의해 개별적으로 분류되고, 최종 잎 노드에서 얻어진 클래스 분포들을 평균하여 주어진 깊이의 단일 트리보다 더 정확한 예측 결과를 제공한다.

Design Parameters of Random forest

Figure 5.11

랜덤 포레스트는 정확도, 일반화 성능, 시간/공간 복잡도를 향상시킬 수 있는 몇 개의 하이퍼 파라미터를 가진다.

트리의 깊이 : $D$
트리의 수 : $T$
샘플링 된 데이터 수 : $\rho$

각 트리가 전체 훈련 데이터 중 일부 무작위 샘플 $\rho$만을 사용하기 때문에 노드마다 서로 다른 분할 기준을 가지게 된다. 이렇게 만들어진 다수의 트리를 평균내면 개별 트리보다 더 부드럽고 일반화된 결정 경계를 만들 수 있다.

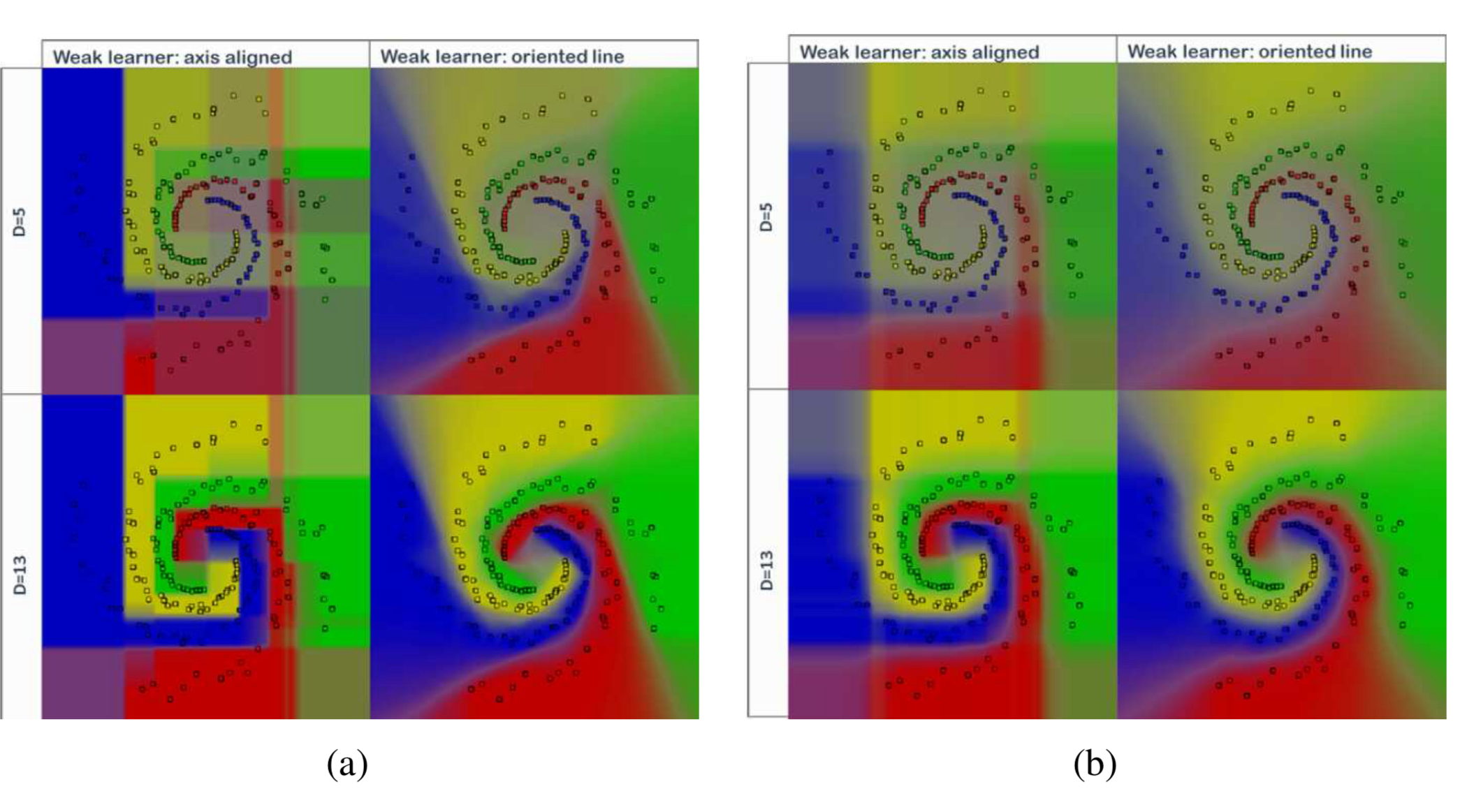
그림 5.11은 간단한 4클래스 2차원 나선형 데이터셋에 대해 일부 하이퍼파라미터가 의사결정 경계에 어떤 영향을 미치는지 보여준다. 트리의 개수는 $T=400$으로 고정되어있다.

(a)와 (b)의 절반은 각각 랜덤성($\rho$)이 미치는 영향을 보여준다. 랜덤성이 적을수록 더 날카롭고 뚜렷한 결정 경계가 만들어지지만, 그만큼 오버피팅의 가능성도 높아진다.

각 그림의 격자에서 위쪽 행은 얕은 트리이고, 아래쪽 행은 깊은 트리로, 결정 경계의 세부묘사는 깊은 트리에서 더 정교하지만, 역시나 오버피팅 위험이 있다. 이는 훈련 데이터에 대한 성능 향상이 곧 일반화 성능과 비례하지만은 않음을 의미한다.

가장 오른쪽 열은 트리 노드에서 사용하는 분할 기준이 축 정렬(axis-aligned)방식이 아니라 특성들의 선형 조합(oblique split)으로 바뀌었을 때 어떤 결과가 나오는지를 보여준다.

파라미터	변화	영향
$\rho$: 샘플링된 데이터 수	큼 → 랜덤성 ↓	결정 경계가 뚜렷, 과적합 위험 ↑
트리 깊이 $D$	큼 → 더 정교한 분할	미세한 경계 가능, 하지만 일반화↓ 가능성
분할 방식	axis-aligned ↔ oblique (선형 조합)	선형 조합은 더 유연한 경계 형성 가능