기초 기하학 요소와 변환

본 섹션에서는 기본적인 2D, 3D 요소와 더불어 3D가 2D평면에 어떻게 투영되는지에 대해 다룬다.

2D 점(Points)

이차원 점(이미지 상의 픽셀 좌표)는 $\mathbb{x}=(x,y) \in \mathbb{R}^2$ 또는

\[\mathbb{x}=\begin{bmatrix} x \\ y \end{bmatrix}\]

로 표현할 수 있다.

이차원 점은 동차 좌표(homogeneous coordinates) $\tilde{\mathbb{x}} = (\tilde{x},\tilde{y},\tilde{w}) \in \mathbb{P}^2$를 사용해 표현할 수 있다.

이때, 크기(scale)만 다른 벡터는 동일한 것으로 간주되며, 이 공간 $\mathbb{P}^2 = \mathbb{R}^3 -(0,0,0)$은 2차원 사영 공간(2D projective space)이라고 부른다.

동차 벡터 $\tilde{x}$는 마지막 원소 $\tilde{w}$로 나누어 비동차 벡터(inhomogeneous vector) $\mathbb{x}$로 변환할 수 있다.

\[\tilde{\mathbb{x}}=(\tilde{x},\tilde{y},\tilde{w}) = \tilde{w}({x}, {y}, 1) = \tilde{w}\bar{\mathbb{x}}\]

여기서 $\tilde{\mathbb{x}}=(x,y,1)$은 보강된 벡터(augmented vector)이다. 또한, 마지막 요소 $\tilde{w}=0$인 동차 점들은 이상점(ideal points) 또는 무한대에 있는 점(points at infinity)이라 불리며, 이는 해당하는 비동차 표현이 존재하지 않는다는 것을 의미한다.

2D 직선(Lines)

이차원 직선은 동차 좌표 $\tilde{\mathbb{I}}=(a,b,c)$로 표현할 수 있다. 상응하는 직선 방정식은

\[\bar{\mathbb{x}}\cdot \tilde{\mathbb{I}}=ax +by + c = 0\]

이다.

직선 방정식 벡터를 정규화 하면 $\mathbb{I}=(\hat{n_x}, \hat{n_y}, d) = (\hat{n}, d)$와 같이 표현할 수 있으며, $\lVert \hat{n} \rVert = 1$(단위 벡터)이다. 이때 $\hat{n}$은 직선에 수직인 법선 벡터(normal vector perpendicular to line)이며, $d$는 그 직선이 원점으로부터 떨어진 거리이다.

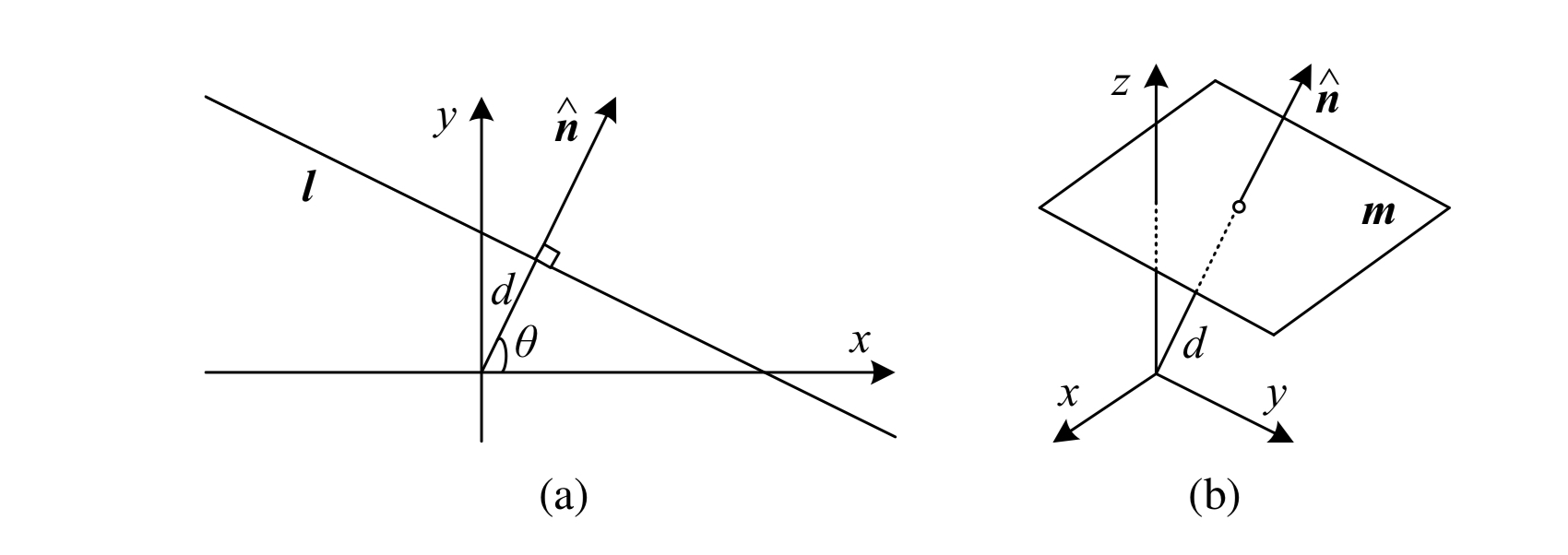
또한 우리는 법선 벡터 $\hat{n}$을 회전각 $\theta$의 함수 $\hat{n}=(\hat{n_x},\hat{n_y})=(\cos\theta, \sin\theta)$ 로 표현할 수 있다(위 그림의 a). 이 표현 방식은 허프 변환 선 탐지 알고리즘에서 사용된다(section 7.4.2링크 추가). $(\theta, d)$ 조합은 극좌표계(poloar coordinates)라고도 부른다.

동차 좌표에서 두 직선의 교점을 다음과 같이 표현할 수 있다.

\[\tilde{\mathrm{x}} = \tilde{\mathrm{l_1}} \times \tilde{\mathrm{l_2}}\]

이때, $\times$는 벡터의 외적 연산자이다. 마찬가지로, 두 점을 잇는 직선은 다음과 같이 표현할 수 있다.

\[\tilde{\mathrm{I}} = \tilde{\mathrm{x_1}} \times \tilde{\mathrm{x_2}}\]

여러 개의 직선에 하나의 교점을 맞추거나, 반대로 여러 개의 점에 하나의 직선을 맞추려고 할 때는 최소제곱법(leastsquares method)를 사용할 수 있다.(section8.1.1링크 추가)

2D 원뿔(Conics)

다른 대수적(algebraic) 곡선들도 간단한 다항식의 동차 방정식을 통해 표현할 수 있다. 그 예로, 원뿔 곡선(conic sections)은 다음과 같은 2차 곡선(quadratic equation)으로 표현 할 수 있다.

\[\tilde{\mathrm{x}}^\top Q \tilde{\mathrm{x}}=0\]

3D 점(Points)

삼차원에 속하는 점 좌표는 비동차 좌표 $\mathrm{x}=(x,y,z)\in \mathbb{R}^3$ 또는 동차 좌표 $\tilde{\mathrm{x}}=(\tilde{x}, \tilde{y}, \tilde{z}, \tilde{w})\in\mathbb{P}^3$로 표현할 수 있다. 종종 3D점을 보강된 벡터 $\bar{\mathrm{x}}=(x,y,z,1)$로 표현하는 것도 유용하다(이때, $\tilde{\mathrm{x}}=\tilde{w}\bar{\mathrm{x}}$).

3D 평면(Planes)

삼차원 평면은 동차 좌표 $\tilde{m} = (a,b,c,d)$를 통해 평면 방정식으로 나타낼 수 있다.

\[\bar{\mathrm{x}} \cdot \tilde{m} = ax + by + cz + d = 0\]

또한 평면 방정식을 다음과 같이 정규화 할 수 있다.

\[\mathrm{m}=(\hat{n_x}, \hat{n_y}, \hat{n_z}, d)=(\hat{\mathrm{n}}, d), \quad \lVert \hat{\mathrm{n}} \rVert = 1\]

이 때, $\hat{\mathrm{n}}$은 평면에 수직인 단위 법선 벡터(normal vector perpendicular to the plane)이며, $d$는 원점으로부터 평면 까지의 거리이다. 2D 직선의 경우와 마찬가지로, 모든 무한대의 점들을 포함하는 무한평면(plane at infinity) $\tilde{\mathrm{m}} = (0,0,0,1)$은 고유한 법선이나 유한한 거리를 갖지 않기에 정규화 할 수 없다

$\hat{\mathrm{n}}$을 두 각도 $(\theta, \phi)$의 함수로 표현할 수 있다. ($\theta$ : 구면좌표계에서의 방위각(azimuthal angle),$\phi$ : 구면좌표계에서의 고도각(elevation angle))

\[\hat{\mathrm{n}} = (\cos{\theta}\cos{\phi},\sin{\theta},\cos{\phi},\sin{\phi})\]

이는 구면 좌표계(spherical coordinates)를 사용하는 방식이지만, 법선 벡터 공간을 균일하게 샘플링하지 않기 때문에 극 좌표계보다 덜 사용된다.

3D 직선(Lines)

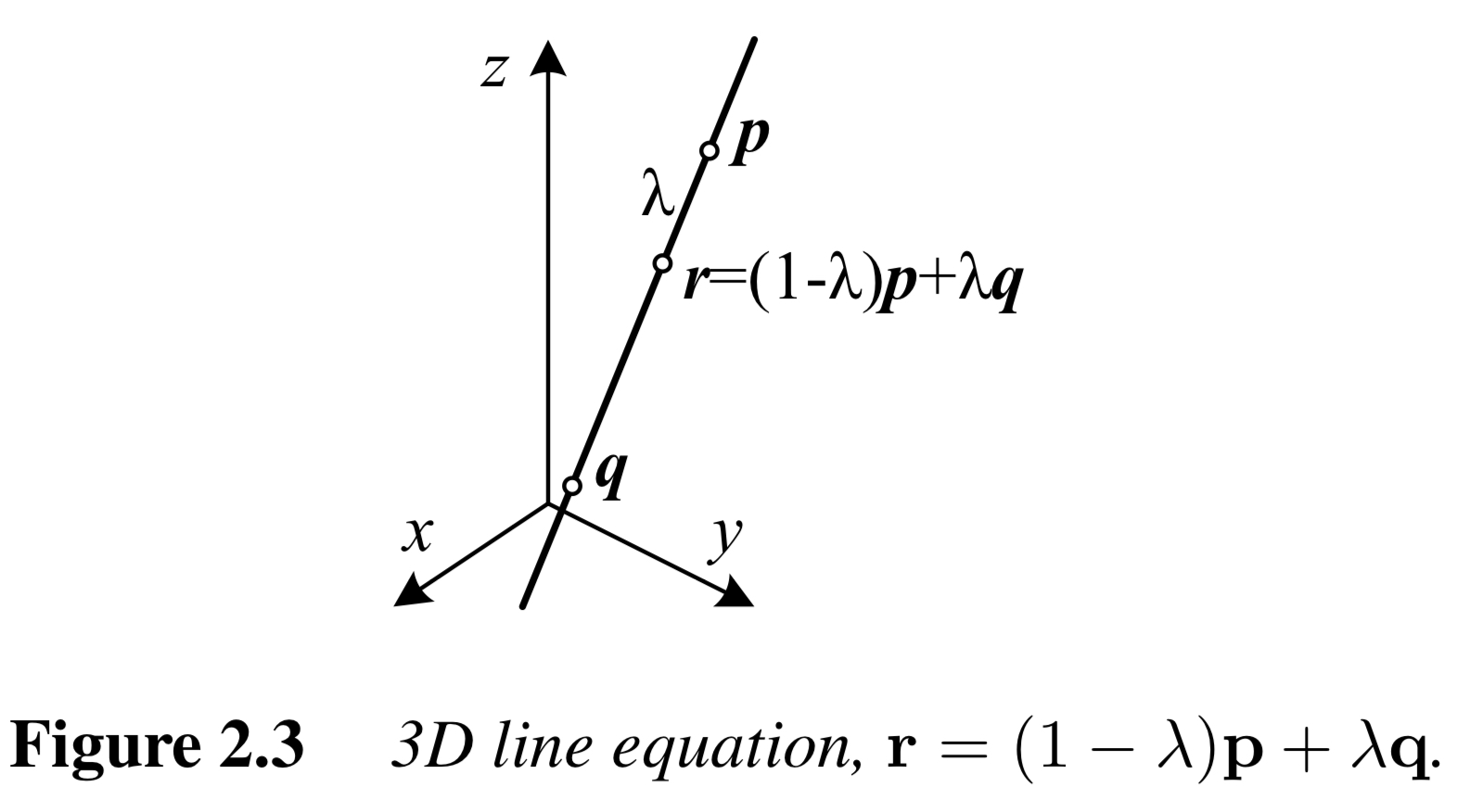
3D 공간상의 직선은 2D 공간에서의 직선이나 3D 공간에서의 평면보다 표현하기 더 까다롭다. 첫직선 위의 두 점 $\mathrm{p, q}$를 활용하면 직선 위의 다른 모든 점은 이 두 점의 선형 결합으로 표현될 수 있다.

\[\mathrm{r} = (1-\lambda)\mathrm{p}+\lambda\mathrm{q}\]

Figure2.3에서 볼 수 있듯이 $0 \le \lambda \le 1$로 제한하면 두 점 $\mathrm{p,q}$를 잇는 선분(line segment)이 된다.

동차 좌표를 사용하면 다음과 같이 직선을 표현할 수 있다.

\[\tilde{\mathrm{r}} = \mathrm{\mu\tilde{p}+\lambda\tilde{q}}\]

특수한 경우는 두 번째 점이 다음과 같이 무한대에 위치하는 경우이다.

\[\tilde{\mathrm{q}} = (\hat{d}_1,\hat{d}_2,\hat{d}_3,\hat{d}_4) = (\hat{\mathrm{d}},0)\]

이 경우에 $\hat{\mathrm{d}}$은 직선의 방향 벡터를 나타내고, 따라서 비동차 3D 직선 방정식을 다음처럼 다시 쓸 수 있다.

\[\mathrm{r=p+\lambda\hat{d}}\]

3D 직선을 양 끝점으로 표현하는 방식의 단점은 너무 많은 자유로운 각도(degrees of freedom)을 가진다는 점이다. 각각의 끝점에 대해 3차원씩 총 6개의 자유각을 갖지만, 실제 3D 직선은 4개의 자유각만 갖는다.

하지만, 두 점이 특정 평면에 있다고 가정하면, 자유각을 4개로 줄일 수 있는데, 거의 수직인 직선을 나타낼 경우 $z=0, z=1$ 평면을 사용해 각 평면상의 ($x,y$)좌표를 직선을 정의하는데 사용할 수 있다. 이런 2-평면 파라미터화(two-plane parameterization)은 빛장(light field)이나 Lumigraph 같은 이미지 기반 렌더링 시스템에서 활용된다. 또한 두 끝점을 사용하는 표현은, 실제 끝점이 명확히 보이지 않고 추정만 가능한 경우에 선분 표현에도 유용하다.

만약 특정 방향에 대해 편향 없이 모든 가능한 직선을 표현하고자 한다면 Plücker 좌표계를 사용할 수 있다. Plücker 좌표는 다음과 같은 $4\times4$ 스큐 대칭 행렬(skew symmetric matrix)의 6개의 독립적인 비영 값(independent non-zero entries)을 의미한다.

\[\mathrm{L=\tilde{p}\tilde{q}^\top-\tilde{q}\tilde{p}^\top}\]

여기서 $\tilde{p},\tilde{q}$는 직선 위의 임의의 서로 다른 두 점이다. 이 표현은 오직 4개의 자유각만 가지며 $\mathrm{L}$은 동차표현이고, $\mathrm{L}=0$을 만족하므로 Plücker 좌표에 대한 이차 제약 조건(quadratic constraint)를 유도한다.

2D 변환(transformations)

평행이동(Translation)

어떤 점 $\mathbf{x}$를 벡터$t$ 만큼 2차원 평행이동을 시행하면 $\mathbf{x}’ = \mathbf{x} + \mathbf{t}$ 또는 행렬 곱 형태

\[\begin{align} \mathbf{x}' &= \begin{bmatrix}\mathbf{I} & t\end{bmatrix} \bar{\mathbf{x}} \\ &= \begin{bmatrix} 1&0&t_x \\ 0 & 1 & t_y \end{bmatrix} \begin{bmatrix}x \\ y \\ 1\end{bmatrix} =\begin{bmatrix}x+t_x \\ y+t_y\end{bmatrix} \end{align}\]

또는 동차좌표계 전체 표현방식인

\[\bar{\mathbf{x}}'=\begin{bmatrix} \mathbf{I} & t \\ 0^\top & 1 \end{bmatrix}\bar{\mathbf{x}}\]

로 표현할 수 있으며, 이때 $\mathbf{I}$는 $2\times2$ 단위벡터, $0^\top$은 영벡터이다.

$2\times3$ 행렬 표현은 간결하게 표기할 때 유용하지만, $3\times3$ 행렬을 사용하면 여러 변환을 행렬 곱으로 체인(chain)이 가능하며, 역변환 계산도 가능하다.

동차 좌표계를 사용하는 이유는 변환 전후 모두 $\bar{\mathbf{x}}$ 형식을 유지하면 일관성 있게 행렬 연산을 통일할 수 있으며, 어떤 식이든 동차 벡터 $\bar{\mathbf{x}}$가 양쪽에 있다면, 일반 벡터 $\mathbf{x}$ 대신 $\bar{\mathbf{x}}$로 대체가 가능하다.

회전과 평행이동(Rotation+Translation)

2D rigid body motion 또는 (유클리드 거리가 보존되기에) 2D Euclidean transformation 라고도 불리는 회전과 평행이동의 결합은 $\mathbf{x’=Rx+t}$ 또는

\[\mathbf{x' = [R \quad t] \bar{x}, \qquad R=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}}\]

로도 표현할 수 있다. 이때 $\mathbf{RR^\top=I,\quad |R|=1}$인 정규 직교 회전 행렬이다.

유사변환 (Scaled rotation, Similarity transform)

유사변환은 $\mathbf{x’=sRx + t}$로 표현할 수 있으며, $\mathbf{s}$는 임의의 스케일 펙터(scale factor)이다. 유사변환은 다음과도 같이 기술할 수 있다.

\[\mathbf{x'=\begin{bmatrix} sR & t \end{bmatrix}\bar{x}=}\begin{bmatrix}a & -b & t_x \\ b & a & t_y\end{bmatrix}\mathbf{\bar{x}}\]

이때 $a^2+b^2=s^2$ 조건만 충족하면 되며, $a^2+b^2=1$일 필요는 없다. 또한 유사변환은 각도와 형상(비율)을 유지한다.

요약하자면 회전 + 이동 + 비율 유지의 역할을 한다.

아핀 변환(Affine)

아핀 변환은 $\mathbf{x’=A\bar{x}}$로 표기하며 이때 $A$는 임의의 $2\times3$ 행렬이다. 예를 들면 다음과 같다.

\[\mathbf{x'}=\begin{bmatrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{bmatrix} \mathbf{\bar{x}}\]

아핀 변환은 직선은 직선으로, 평행선은 평행선으로 이동되며 이는 선형 공간 구조를 보존한다는 의미를 갖는다. 다만 원근효과를 갖지는 않는다.

요약하자면 선형 변환 + 이동의 역할을 한다.

사영 변환 (Projective)

perspective transform 또는 _homography_로도 불리는 사영 변환은 $\mathbf{\tilde{x}’=\tilde{H}\tilde{x}}$로 표기하며 이때 $H$는 임의의 $3\times3$ 동차행렬이다.

변환 결과인 동차 좌표 $\mathbf{\tilde{x}’}=[x,y,1]^\top$는 정규화를 거쳐야 비동차 좌표 $\mathbf{x}$를 얻을 수 있다.

\[x’ = \frac{h_{00}x + h_{01}y + h_{02}}{h_{20}x + h_{21}y + h_{22}},\quad y’ = \frac{h_{10}x + h_{11}y + h_{12}}{h_{20}x + h_{21}y + h_{22}}\]

사영 변환은 원근 왜곡(perspective distortion) 표현이 가능하며 직선은 여전히 직선으로 이동하지만, 평행성과 거리, 각도는 보존되지 않는다.

요약

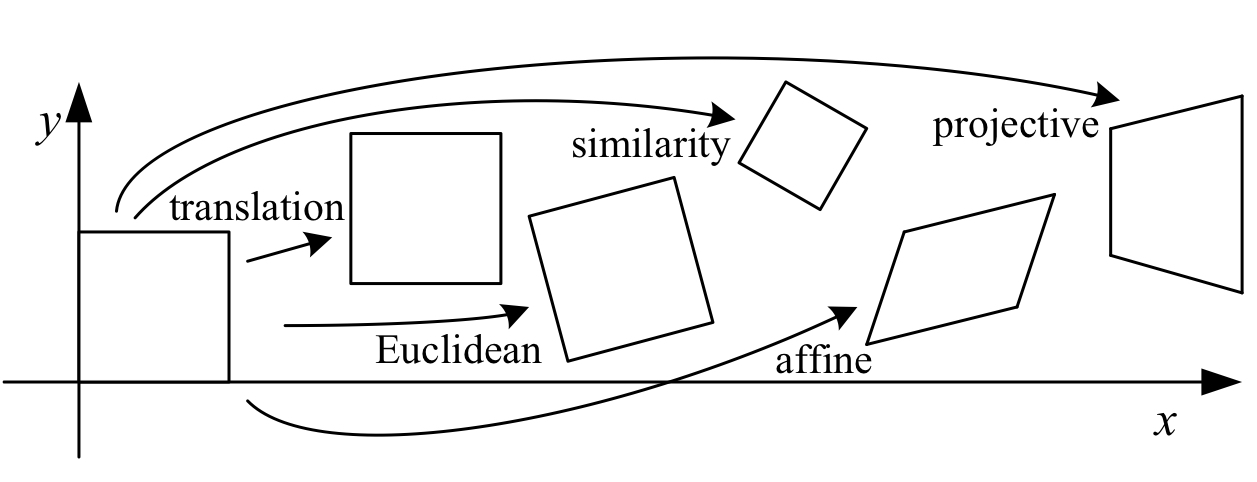
컴퓨터 비전에서 이미지의 위치나 구조를 바꾸기 위해 자주 쓰이는 변환은 다음 세 가지로 분류할 수 있다.

• Similarity transform
• Affine transform
• Projective transform

이들 변환은 동차 좌표 상에서 이루어지며, 모두 $3\times3$ 행렬로 표현된다. 특히 이 변환들은 수학적으로 군(Group)을 이루며, 서로 포함(subgroup) 관계를 가진다.

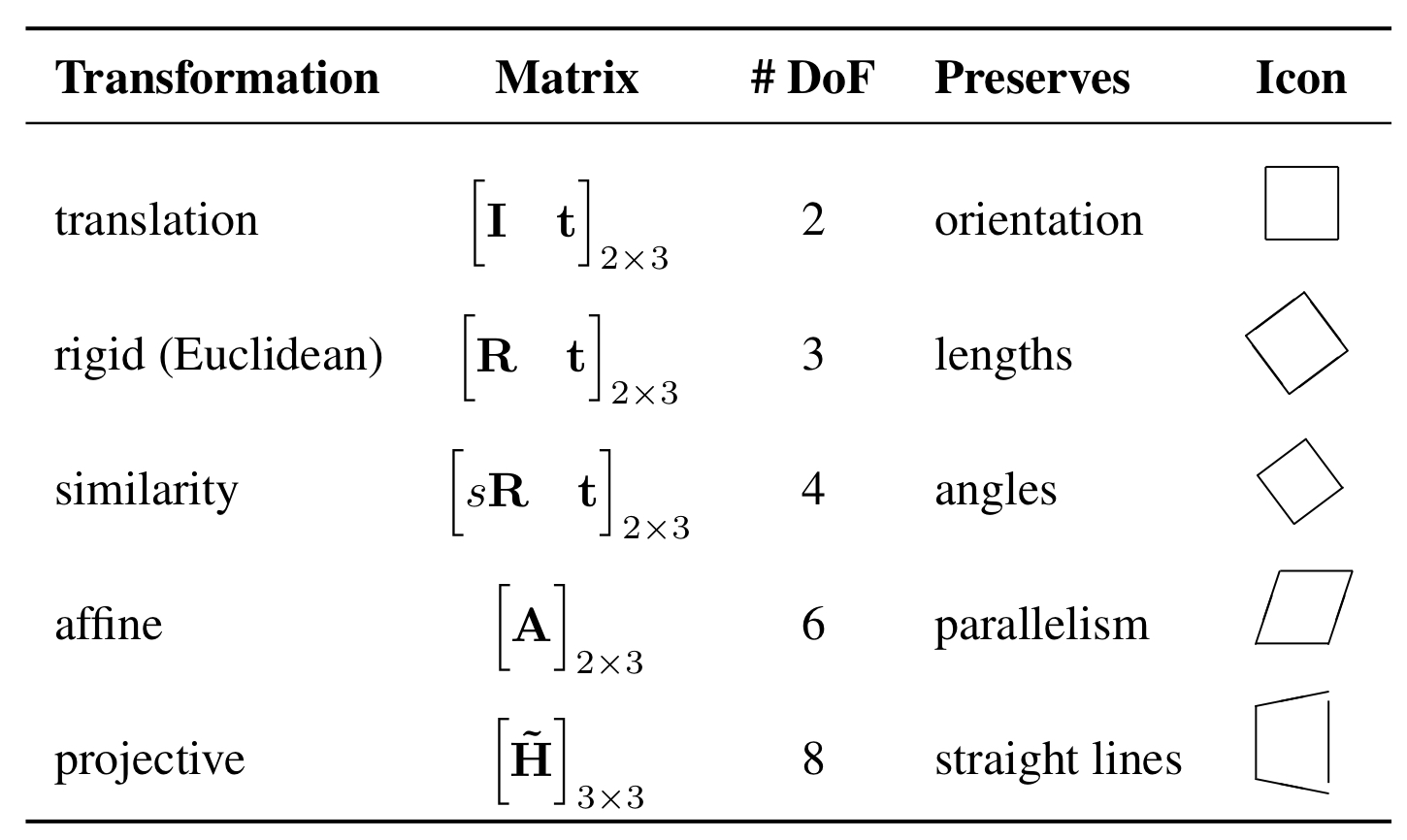
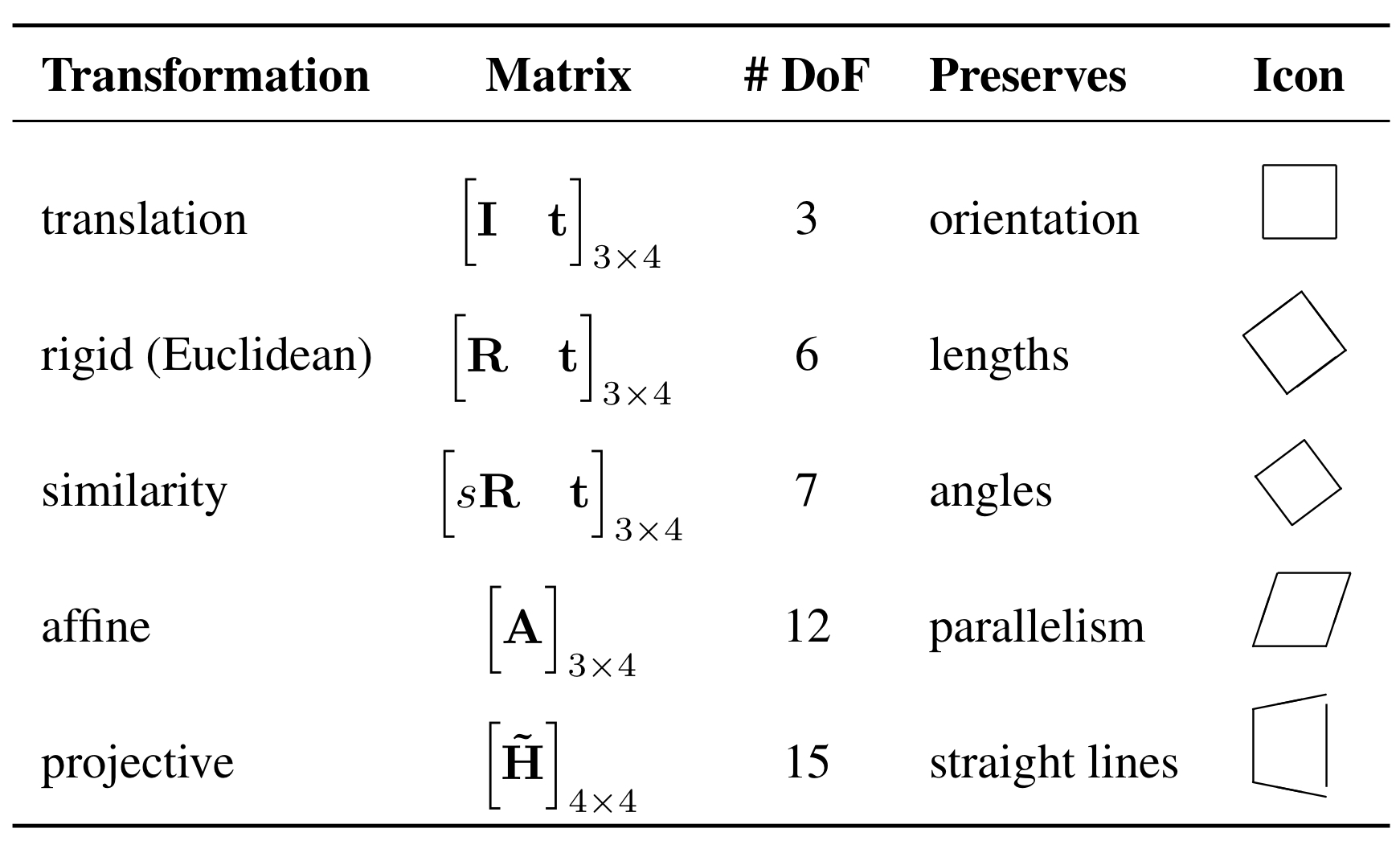
\[\mathrm{Similarity\subset Affine\subset Projective }\]

군 구조는 다음 표 처럼 정리할 수 있다.

군	설명	의미
SO(2)	Special Orthogonal Group	2D 회전만 포함
SE(2)	Special Euclidean Group	회전 + 평행이동 포함
Affine Group	일반 아핀 변환 전체	선형 + 이동
Projective Group	전체 사영변환	일반적인 구조

각 변환은 자신과 동일한 종류의 다른 변환과 합성할 수 있으며, 당연히 그 역변환도 존재한다.

Co-vectors

2D 평면에서 좌표 $\mathbf{\tilde{x}}$에 대해 사영 변환을 적용할 수 있으면, 직선 방정식에도 동일한 방식으로 변환을 적용할 수 있을까?

예를 들어 동차 좌표계 선형 방정식 $\mathbf{\tilde{l}\cdot\tilde{x}}$을 생각해보자($\mathbf{\tilde{l}}$은 직선을 나타내는 공벡터이고, $\mathbf{\tilde{x}}$는 점이다). 점이 사영 변환에 따라 $\mathbf{\tilde{x}’=\tilde{H}\tilde{x}}$로 변환된다면, 직선에 해당하는 식도 다음과 같이 전개된다.

\[\tilde{\mathbf{l}}’ \cdot \tilde{\mathbf{x}}’ = \tilde{\mathbf{l}}’^{\top} \tilde{\mathbf{H}} \tilde{\mathbf{x}} = (\tilde{\mathbf{H}}^{\top} \tilde{\mathbf{l}}’)^{\top} \tilde{\mathbf{x}} = \tilde{\mathbf{l}} \cdot \tilde{\mathbf{x}} = 0\]

따라서 공벡터의 변환은 다음과 같다.

\[\mathbf{\tilde{l}'=\tilde{H}^{-\top}\tilde{l}}\]

즉, 사영 변환이 공벡터(2D 직선 또는 3D 법선 벡터)에 작용할 때는, 변환 행렬의 전치 역행렬을 사용해서 표현해야 한다. 이러한 표현은 사영 변환 행렬 $\mathbf{\tilde{H}}$가 동차행렬이기 때문에 결국 여인자 행렬(adjoint)을 사용한 것과 동등하다.

늘리기/찌그러뜨리기 (Stretch/squash)

이 변환은 이미지의 종횡비(aspect ratio)를 변형시킨다.

\[\begin{gather} x'=s_xx+t_x \\ y'=s_yy+t_y \end{gather}\]

아핀 변환의 제한된 형태이며, 상술한 군 구조들에 부합하지는 않는다.

평면 표면 흐름 변환 (Planar surface flow)

\[\begin{gather} x'=a_0+a_1x+a_2y+a_6x^2+a_7xy \\ y'=a_3+a_4x+a_5y+a_6xy+a_7y^2 \end{gather}\]

여덟 개의 파라미터를 가지는 변환은 평면 표면이 약간의(small) 3차원 운동을 할 때 발생하며, 전역적인 호모그래피(full homography)에 대한 소운동 근사(small motion approximation)로 해석할 수 있다.

이 방식의 장점은 변환 파라미터 $a_k$들에 대해 선형적이라는 점이며, 이 파라미터들은 일반적으로 우리가 추정하고자 하는 값이다.

쌍선형 보간 변환 (Bilinear interpolant)

\[\begin{gather} x’ = a_0 + a_1 x + a_2 y + a_6 x y \\ y’ = a_3 + a_4 x + a_5 y + a_7 x y \end{gather}\]

이는 정사각형의 네 꼭짓점 움직임에 따른 변형을 보간(interpolate)하는 데 사용될 수 있으며, 네 개의 공선이 아닌 점들의 움직임도 보간할 수 있다.

이 변환은 motion parameter들에 대해 선형적이지만, 일반적으로 직선은 보존하지 않으며, 정사각형 축에 평행한 선만 유지된다. 또한 산재한 그리드(sparse grids) 보간에 매우 유용하게 사용된다.(9.2.2절 링크 추가)

3D 변환

평행이동 (Translation)

어떤 점 $\mathbf{x}$를 벡터$t$ 만큼 3차원 평행이동을 시행하면 $\mathbf{x}’ = \mathbf{x} + \mathbf{t}$ 또는 행렬 곱 형태

\[\begin{align} \mathbf{x}' &= \begin{bmatrix}\mathbf{I} & t\end{bmatrix} \bar{\mathbf{x}} \\ \end{align}\]

로 표현할 수 있으며, 이때 $\mathbf{I}$는 $3\times3$ 단위벡터이다.

회전과 평행이동 (Rotation+Translation)

3D 강체 운동(3D rigid body motion) 또는 3D 유클리드 변환(3D Euclidean transformation) 또는 SE(3)라고도 불리는 이 변환은 $\mathbf{x’=sRx + t}$ 또는

\[\mathbf{x' = [R \quad t] \bar{x}}\]

로 표현할 수 있다. 여기서 $\mathbf{R}$은 $\mathbf{RR^\top=I, \quad |R|=1}$을 만족하는 $3\times3$ 정규 직교 회전 행렬(_orthonormal rotation matrix)이다.

경우에 따라 다음 형태로 표현하는 것이 더 편리할 수 있다.

\[\mathbf{x}’ = \mathbf{R}(\mathbf{x} - \mathbf{c}) = \mathbf{R} \mathbf{x} - \mathbf{R} \mathbf{c}\]

여기서 $\mathbf{c}$는 회전의 중심을 의미하며 종종 카메라의 중심을 뜻하기도 한다.

유사변환(Scaled rotation)

3D 유사 변환 (3D similarity transform)은 $\mathbf{x’=sRx + t}$로 표현될 수 있으며, $\mathbf{s}$는 임의의 스케일 펙터(scale factor)이다. 유사변환은 다음과 같은 행렬 형태로도 기술할 수 있다.

\[\mathbf{x'=\begin{bmatrix} sR & t \end{bmatrix}\bar{x}}\]

이 변환은 2차원 유사 변환에서와 마찬가지로 직선과 평면 사이의 각도를 보존한다.

아핀변환 (Affine)

아핀 변환은 $\mathbf{x’=A\bar{x}}$로 표기하며 이때 $A$는 임의의 $3\times4$ 행렬이다. 예를 들면 다음과 같다.

\[\mathbf{x}’ = \begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \end{bmatrix} \bar{\mathbf{x}}\]

아핀 변환에서는 평행한 직선과 평면이 그대로 평면을 유지한다.

사영변환 (Projective)

3D 원근 변환(3D perspective transform), homography, 또는 공선변환(collineation)이라고 불리는 사영 변환은 동차 좌표계에서 다음과 같이 기술된다.

\[\tilde{\mathbf{x}}’ = \tilde{\mathbf{H}} \tilde{\mathbf{x}}\]

이때 $H$는 임의의 $4\times4$ 동차행렬이다.

2차원의 경우와 마찬가지로 변환된 벡터는 비동차 좌표계 결과 $\mathbf{x}$를 얻기 위해 정규화 되어야 하며, 사영 변환은 직진성을 유지한다.

3D 회전 (3D Rotation)

축/각 (Axis/Angle)

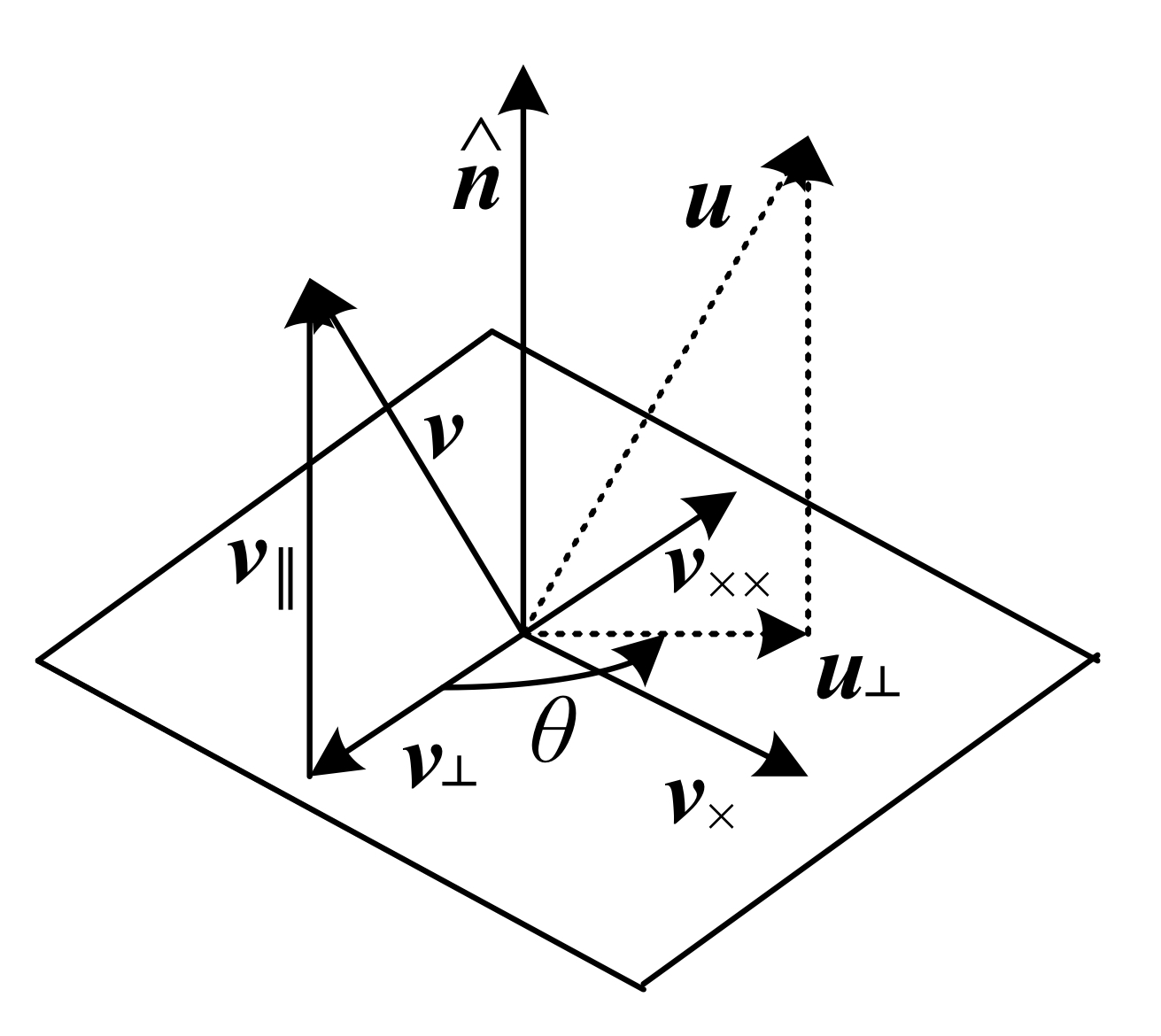
회전은 회전각 $\mathbf{\hat{n}}$과 $\theta$ 또는 삼차원 벡터 $\mathbf{\omega=\theta\hat{n}}$으로 표현할 수 있다. 그림 2.5는 등적 변환을 계산하는 방법에 대해서 표현되어 있는데, 수식으로 자세히 기술해보자.

먼저 벡터 $\mathbf{v}$를 회전 축 $\mathbf{\hat{n}}$ 위로 정사영하면 다음과 같다.

\[\mathbf{V_\parallel=\hat{n}(\hat{n}\cdot v)=(\hat{n}\hat{n}^\top)v}\]

이 성분은 회전에 영향을 받지 않는 부분이다. 다음으로 $\mathbf{v}$에서 $\mathbf{\hat{n}}$방향으로의 수직 잔여(perpendicular residual) 벡터를 구하면 다음과 같다.

\[\mathbf{v_\perp=v-v_\parallel=(I-\hat{n}\hat{n}^\top)v}\]

이제 이 벡터를 90도 회전시키기 위해 벡터의 외적을 사용한다.

\[\mathbf{v_\times=\hat{n}\times v_\perp=\hat{n}\times v=[\hat{n}]_\times v}\]

(이 때, $\mathbf{v=v_\parallel+v_\perp}$이며, 평행한 두 벡터의 외적은 0이기 때문에 $\mathbf{\hat{n}\times v_\parallel=0}$이므로 $\mathbf{\hat{n}\times v_\perp=\hat{n}\times v}$. 또한, $[\hat{n}]_\times$는 벡터 $\mathbf{\hat{n}}=(\hat{n_x}, \hat{n_y}, \hat{n_z})$에 대한 외적 연산을 행렬로 표현한 것이다.)

\[[\hat{\mathbf{n}}]_{\times} = \begin{bmatrix} 0 & -\hat{n}_z & \hat{n}_y \\ \hat{n}_z & 0 & -\hat{n}_x \\ -\hat{n}_y & \hat{n}_x & 0 \end{bmatrix}\]

여기서 벡터를 다시 한 번 90도 회전시키는 것은 외적을 한번 더 수행하는 것과 동일하다.

\[\mathbf{v}_{\times \times} = \hat{\mathbf{n}} \times \mathbf{v}_{\times} = [\hat{\mathbf{n}}]^2_{\times} \mathbf{v} = -\mathbf{v}_{\perp}\]

따라서 다음이 성립한다.

\[\mathbf{v_\parallel=v-v_\perp=v+v_{\times\times}=(I+[\hat{n}]^2_\times)v}\]

이제 회전된 벡터 $\mathbf{u}$의 평면 내 성분을 계산할 수 있다.

\[\mathbf{u}_{\perp} = \cos\theta \mathbf{v}_{\perp} + \sin\theta \mathbf{v}_{\times} = (\sin\theta [\hat{\mathbf{n}}]_{\times} - \cos\theta [\hat{\mathbf{n}}]^2_{\times}) \mathbf{v}\]

위에서 계산된 모든 성분을 종합하여 최종적으로 회전된 벡터 $\mathbf{u}$는 다음과 같다.

\[\mathbf{u} = \mathbf{u}_{\perp} + \mathbf{v}_{\parallel} = (\mathbf{I} + \sin\theta [\hat{\mathbf{n}}]_{\times} + (1 - \cos\theta)[\hat{\mathbf{n}}]^2_{\times}) \mathbf{v}\]

따라서 $\hat{n}$축을 중심으로 $\theta$만큼 회전하는 회전 행렬은 다음과 같이 쓸 수 있으며 로드리게즈 공식(Rodrigues’ formula)로도 알려져 있다.

\[\mathbf{R}(\hat{\mathbf{n}}, \theta) = \mathbf{I} + \sin\theta [\hat{\mathbf{n}}]_{\times} + (1 - \cos\theta) [\hat{\mathbf{n}}]^2_{\times}\]

다만 회전축과 각도를 활용한 위 표현은 삼차원 회전을 위한 최소 표현에 불과하다. 다만 $\theta$가 도 단위가 아니라 라디안으로 표현되었을 때, 특히나 미세한 정도의 작은 회전에서는 매우 적합한 방식이다. 그러나 360도 또는 $2\pi$의 배수를 더해도 동일한 회전을 만들며, $(\hat{n},\theta)$와 $(-\hat{n},-\theta)$도 같은 회전을 나타내기에 유일한 표현은 아니다.

상술했던 작은 회전의 경우에 로드리게즈 공식은 다음처럼 단순화 할 수 있다.

\[\mathbf{R}(\boldsymbol{\omega}) \approx \mathbf{I} + \sin\theta [\hat{\mathbf{n}}]_{\times} \approx \mathbf{I} + [\boldsymbol{\omega}]_{\times} = \begin{bmatrix} 1 & -\omega_z & \omega_y \\ \omega_z & 1 & -\omega_x \\ -\omega_y & \omega_x & 1 \end{bmatrix}\]

위 행렬은 회전 파라미터 $\omega$와 회전행렬 $\mathbf{R}$사이의 선형화된 관계를 제공한다.

또한 벡터 $\mathbf{v}$에 대해 $\mathbf{R}(\boldsymbol{\omega})\mathbf{v} \approx \mathbf{v} + \boldsymbol{\omega} \times \mathbf{v}$로 근사할 수 있고, 이것은 $\mathbf{Rv}$를 $\omega$에 대해 편미분할 때 유용하다.

\[\frac{\partial (\mathbf{R}\mathbf{v})}{\partial \boldsymbol{\omega}^T} = -[\mathbf{v}]_{\times} = \begin{bmatrix} 0 & z & -y \\ -z & 0 & x \\ y & -x & 0 \end{bmatrix}\]

지수 꼬임(exponential twist)를 통해서도 고정된 각도 회전을 유도할 수 있다. $\theta$각도만큼 회전하는 것은 $\theta/k$각도의 회전을 $k$번 반복하는 것과 동일하므로 다음과 같은 극한 표현을 사용할 수 있다.

\[\mathbf{R(\hat{n},\theta)=\lim_{k\to\infty}(I+\frac{1}{k}[\theta\hat{n}]_\times)^k=\exp[\omega]_\times}\]

여기서 행렬 지수 $\exp([\omega]_\times)$ 는 다음과 같이 테일러 급수로 전개할 수 있으며, 이는 로드리게스(Rodrigues) 공식이다. (이때, \(\mathbf{[\hat{n}]^k_\times = -[\hat{n}]^{k+2}_\times}, \ k > 0\), $\theta$ 는 라디안으로 가정.)

\[\begin{align} \exp([\boldsymbol{\omega}]_{\times}) &= \mathbf{I} + \theta[\hat{\mathbf{n}}]{\times} + \frac{\theta^2}{2}[\hat{\mathbf{n}}]^2_{\times} + \frac{\theta^3}{3!}[\hat{\mathbf{n}}]^3_{\times} + \cdots\\ &= \mathbf{I + (\theta-\frac{\theta}{3!}+\cdots)[\hat{n}]_\times+(\frac{\theta^2}{2}-\frac{\theta^4}{4!}+\cdots)[\hat{n}]_\times^2}\\ &=\mathbf{I} + \sin\theta [\hat{\mathbf{n}}]_{\times} + (1 - \cos\theta)[\hat{\mathbf{n}}]^2_{\times}, \\ \\ \mathbf{[v]^2_\times} &= \begin{bmatrix} -y^2-z^2 & xy & xz \\ xy & -x^2-z^2 & yz \\ xz & yz & -x^2-y^2 \end{bmatrix} \end{align}\]

Unit quaternions

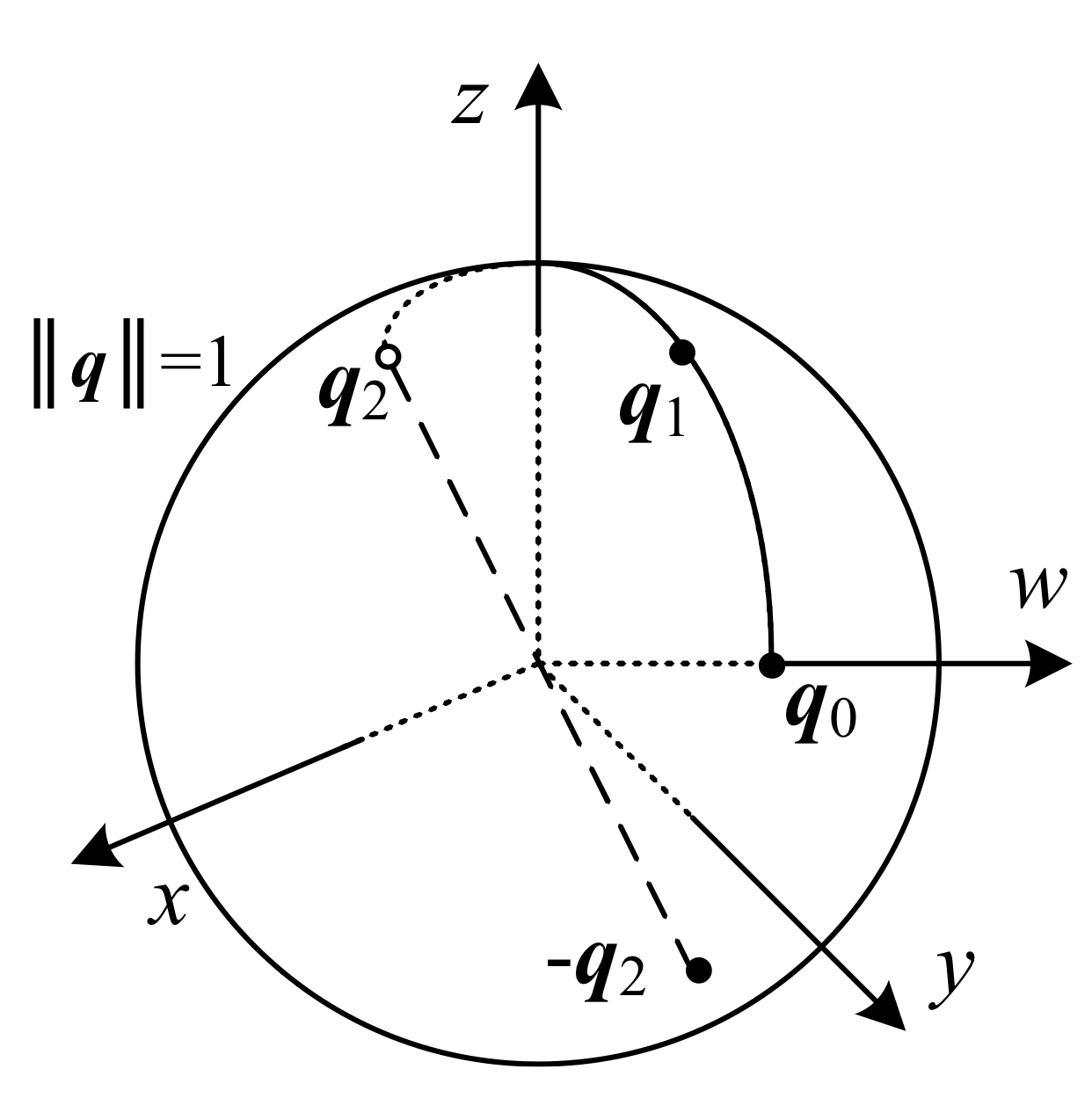
Quaternions은 복소수를 확장한 4차원 수 체계로 다음과 관계로 구성된다.

\(\begin{gather} q = w+xi+yj+zk, \quad w,x,y,z \in \mathbb{R}, \quad i^2=j^2=k^2 = -1 \\ ij = k,\ jk=i,\ ki=j, \\ ji = -k, \ kj = -i \ ik = -j \end{gather}\) 이때 세 단위 허수의 제곱은 -1 이지만, 세 항의 순차적인 곱은 -1이므로 순서에 주의해야 한다.

Unit Quaternions는 노름이 1인 쿼터니언 $q$를 의미한다. 즉, 길이가 1인 쿼터니언이다.

\[\lVert q \rVert = \sqrt{w^2 + x^2 + y^2 + z^2} = 1\]

Unit Quaternion은 길이가 1인 4차원 벡터 $q = (q_x,q_y,q_z,q_w) = (x,y,z,w)$로 표현된다. 부호가 반대인 쿼터니언 $q, -q$는 동일한 회전 표현을 나타내며 이를 dual covering라고 부른다. dual covering을 제외하면 단위 쿼터니언을 통한 회전 표현은 유일하며, 연속적이다. 예를 들면, 회전 행렬이 연속적으로 변화할 때 이에 대응하는 쿼터니언 경로도 존재하며, 구면 위를 완전히 한 바퀴 돌아 원점 $q_0=(0,0,0,1)$로 돌아올 수 있다.

쿼터니언은 [[#축/각 (Axis/Angle)]] 표현을 이용해 다음과 같은 공식으로부터 도출할 수 있으며, $\hat{n}, \theta$는 각각 회전축과 회전 각도를 의미한다.

\[\mathbf{q} = (\mathbf{v},w)=\mathbf{(\sin{\frac{\theta}{2}\hat{n},\cos{\frac{\theta}{2}}})}\]

위 식을 삼각 함수 항등식 $\sin{\theta}=2\sin{\frac{\theta}{2}\cos{\frac{\theta}{2}}}$와 $1-\cos{\theta}=2\sin^2\frac{\theta}{2}$를 활용하면 로드리게즈 공식을 다음과 같이 표현할 수 있다.

\[\begin{align} \mathbf{R(\hat{n},\theta)} &= \mathbf{I+\sin\theta[\hat{n}]_\times+(1-\cos\theta)[\hat{n}]^2_\times} \\ &=I +2w\mathbf{[v]_\times + 2[v]^2_\times} \end{align}\]

일련의 외적, 스케일 조정, 덧셈 연산으로 구성되어 벡터 v를 쿼터니언을 사용해 빠르게 회전시키는 방법을 제안한다. 쿼터니언 성분$(x,y,z,w)$에 대해 회전 행렬 $\mathbf{R(q)}$를 표현하기 위해 [[#축/각 (Axis/Angle)]]에서 사용되었던 다음 항등식을 사용한다.

\[[\mathbf{v}]_\times = \begin{bmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{bmatrix}, \quad [\mathbf{v}]^2_\times = \begin{bmatrix} -y^2 - z^2 & xy & xz \\ xy & -x^2 - z^2 & yz \\ xz & yz & -x^2 - y^2 \end{bmatrix}\]

따라서 쿼터니언에 대한 회전 행렬은 다음과 같이 계산된다.

\[\mathbf{R(q)} = \begin{bmatrix} 1 - 2(y^2 + z^2) & 2(xy - zw) & 2(xz + yw) \\ 2(xy + zw) & 1 - 2(x^2 + z^2) & 2(yz - xw) \\ 2(xz - yw) & 2(yz + xw) & 1 - 2(x^2 + y^2) \end{bmatrix}\]

단위 쿼터니언의 가장 큰 장점은 회전을 조합할 때 매우 단순한 대수 구조를 가진다는 점이다.

두 쿼터니언 $\mathbf{q_0=(v_0},w_0), \mathbf{q_1=(v_1},w_1)$에 대해 곱셈은 다음과 같이 정의되며, 이 곱셈은 교환 법칙을 따르지 않는다.

\[\mathbf{q}_2 = \mathbf{q}_0 \mathbf{q}_1 = (\mathbf{v}_0 \times \mathbf{v}_1 + w_0 \mathbf{v}_1 + w_1 \mathbf{v}_0, w_0 w_1 - \mathbf{v}_0 \cdot \mathbf{v}_1)\]

쿼터니언의 역원을 구할 때는 v 또는 w 중 하나의 부호를 바꾸기만 하면 되며, 쿼터니언의 나눗셈 연산은 다음과 같이 정의된다.

\[\mathbf{q}_2 = \mathbf{q}_0 / \mathbf{q}_1 = \mathbf{q}_0 \mathbf{q}_1^{-1} = (\mathbf{v}_0 \times \mathbf{v}_1 + w_0 \mathbf{v}_1 - w_1 \mathbf{v}_0, w_0 w_1 + \mathbf{v}_0 \cdot \mathbf{v}_1)\]

위 연산은 두 회전 간의 점진적 회전(incremental rotation)이 필요할 때 매우 유용하다.

Spherical Linear intERPolation(SLERP)

구면 선형 보간 $slerp(\mathbf{q_0,q_1}, \alpha)$ 알고리즘

1. $\mathbf{q_r=q_1/q_0=(v_r,}w_r)$
2. $if\ w_r < 0 \ then \ \mathbf{q_r}\leftarrow - \mathbf{q_r}$
3. $\theta_r = 2 \tan^{-1}(|\mathbf{v}_r| / w_r)$
4. $\hat{\mathbf{n}}_r = \mathcal{N}(\mathbf{v}_r) = \mathbf{v}_r / |\mathbf{v}_r|$
5. $\theta_\alpha = \alpha \cdot \theta_r$
6. $\mathbf{q}\alpha = \left( \sin\left( \frac{\theta\alpha}{2} \right) \hat{\mathbf{n}}_r, \cos\left( \frac{\theta\alpha}{2} \right) \right)$
7. return \(\mathbf{q}_2 = \mathbf{q}_\alpha \mathbf{q}_0\)

쿼터니언 비율로부터 회전축과 전체 회전 각도를 계산한 후, 보간된 중간 회전 쿼터니언을 계산해 시작 회전 쿼터니언에 곱해 최종 회전을 구할 수 있다.

이 외에도 SLERP를 구현하는 두 가지 다른 수식이 있다.

첫 번째는, 보간 회전 쿼터니언 $\mathbf{q}_r$을 $\alpha$제곱 후 원래 쿼터니언에 곱하는 방식이다.

\[\mathbf{q_2}=\mathbf{q_r^\alpha}\cdot\mathbf{q_0}\]

두 번째는, 쿼터니언을 4차원 구면 상의 벡터로 간주하여 보간하는 방식이다.

\[\mathbf{q}_2 = \frac{\sin((1 - \alpha)\theta)}{\sin \theta} \cdot \mathbf{q}_0 + \frac{\sin(\alpha \theta)}{\sin \theta} \cdot \mathbf{q}_1\]

여기서 $\theta$는 두 쿼터니언 간의 내적(dot product)으로부터 계산한 회전 각이다

\[\theta = \cos^{-1}(\mathbf{q}_0 \cdot \mathbf{q}_1)\]

쿼터니언들은 4차원 벡터이므로, 이 내적은 각 성분 간의 일반적인 내적이다.

이 모든 방법들은 비슷한 결과를 내지만 $\mathbf{q_0, q_1}$이 매우 가까운 경우에는 조심해야 할 필요가 있으며, 회전각을 구할 때 아크 탄젠트를 활용하는 방법도 고려할 수 있다.

3D to 2D projections

Orthography and para-perspective

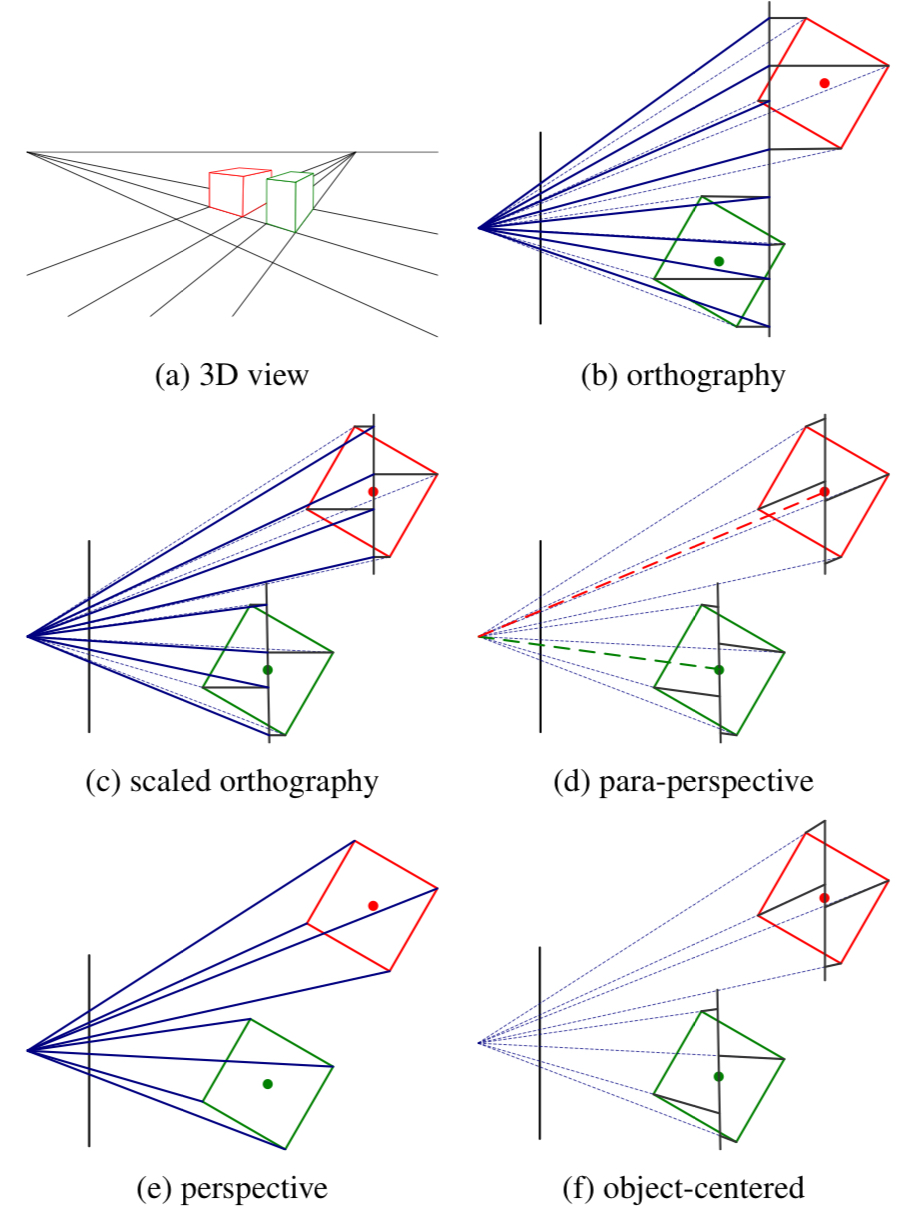
직교 투영법(orthographic projection)을 이용해 3차원 좌표 $\mathbf{P}$에서 2차원 점 $\mathbf{x}$를 얻는 것은 간단하게 $z$값을 덜어주기만 하면 된다.

\[\mathbf{x=[I_{2\times2}\|0]p}\]

동차 좌표계를 활용한 표현법은 다음과 같다.

\[\mathbf{\tilde{x}}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \mathbf{\tilde{p}}\]

직교 투영시에 깊이($z$)는 덜어내지만 동차 좌표($w$)는 유지해서 변환 연산에 사용한다.

직교 투영은 초점 거리가 긴 망원렌즈나 카메라로부터의 거리에 비해 깊이가 얕은 물체들에 대해 근사 모델로 사용되며, 직교 투영 가정이 완벽히 성립하려면 특수한 렌즈를 사용해야한다.

실제로는 일반적으로 미터 단위로 측정되는 월드 좌표계(world coordinates) 값을 이미지 센서 상에 맞게 스케일을 조정해야 한다. 이미지 센서는 물리적으로는 밀리미터 단위이지만, 실제 계산에서는 픽셀 단위로 사용된다. 이러한 이유로 scaled 직교 투영이 실제로는 더 일반적으로 사용된다.

\[\mathbf{x = [s\cdot I_{2\times2}\|0]\cdot p}\]

즉, $\mathbf{x}$좌표는 단순히 상위 2차원 성분에 스케일 $s$를 곱한 값이다.

scaled 직교 투영은 다음과 동일한 방식이다.

1. 월드 좌표를 카메라에 정면으로 평행한 평면으로 먼저 투영
2. 그 이미지를 일반적인 원근 투영 방식으로 스케일링

스케일링은 장면의 모든 부분에 대해 동일하게 적용될 수도(Figure 2.7b), 혹은 독립적으로 모델링된 객체마다 다르게 적용될 수도 있다(Figure 2.7c). 더 중요한 점은 Structure-From-Motion을 수행할 때, 스케일 값이 프레임마다 달라질 수 있고, 이는 물체가 카메라에 가까워짐에 따라 생기는 스케일 변화를 더 잘 모델링할 수 있게 해준다.

scaled 직교 투영은 카메라의 방향을 단순한 최소제곱법으로 추정할 수 있는 것과 같이 일부 계산을 상당히 단순화 하기에 카메라로부터 멀리 떨어진 3D 객체의 형상 복원에 널리 사용된다. 직교 투영 모델을 사용하는 경우 구조(structure)와 모션(motion)을 동시에 추정할 수 있으며, 이때는 특이값 분해(factorization)을 활용한다.

이와 밀접하게 연관된 모델로는 para-perspective모델을 들 수 있는데, 이 모델에서도 객체의 점들은 이미지 평면과 평행한 지역 참조 평면(local reference plane)에 먼저 투영된다. 다만 이미지 평면에 수직인 직교 방향이 아니라, 카메라 중심에서 객체 중심으로 향하는 시선 방향과 평행한 방향을 따른다(Figure 2.7d). 그리고 난 후, 중간 평면으로 투영된 결과는 이미지 평면으로 변환되고, 전체 투영 과정은 아핀 변환으로 표현될 수 있으며, 다음과 같이 수식으로 표현될 수 있다.

\[\tilde{\mathbf{x}} = \begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \tilde{\mathbf{p}}\]

Para-perspective 모델은 scaled 직교 투영보다 더 정확한 투영 모델을 제공하며, 픽셀마다의 per-pixel 나눗셈 같이 복잡한 계산 없이 투영을 수행할 수 있다.

Perspective

컴퓨터 그래픽스와 컴퓨터 비전 분야에서 가장 일반적으로 사용되는 투영은 true 3D perspective(Figure 2.7e)를 들 수있다. 점들은 $z$ 값으로 나누어 이미지 평면으로 투영되는데, 비동차 좌표계에서는 다음과 같이 표현된다.

\[\bar{\mathbf{x}} = \mathcal{P}_z(\mathbf{p}) = \begin{bmatrix} x/z \\ y/z \\ 1 \end{bmatrix}\]

동차 좌표계에서는 좀 더 단순한 선형 형태로 표현될 수 있다.

\[\tilde{\mathbf{x}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \tilde{\mathbf{p}} \tag{2.51}\]

이 모델은 $\mathbf{p}$의 $w$ 성분을 버리므로, 투영 후에는 거리 정보가 소실되고, 이는 2차원 이미지 센서의 특성상 당연하다고 볼 수 있다.

컴퓨터 그래픽스 시스템에서는 일반적으로 다음과 같은 2단계 투영이 사용된다.

1. 3차원 좌표를 정규화된 디바이스 좌표(normalized device coordinates)로 변환 $(x,y,z)\in[-1,1]\times[-1,1]\times[0,1]$
2. 변환된 좌표를 뷰포트 변환을 퉁해 정수형 픽셀 좌표로 다시 스케일링

이 때 투영은 다음과 같은 $4\times 4$행렬로 처리된다.

\[\tilde{\mathbf{x}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -z_{\text{far}}/z_{\text{range}} & z_{\text{near}} z_{\text{far}}/z_{\text{range}} \\ 0 & 0 & 1 & 0 \end{bmatrix} \cdot \tilde{\mathbf{p}}\]

이 때, $z_{near}, z_{far}$은 각각 가깝거나 먼 z-클리핑 평면이고, $z_{range}=z_{far} - z_{near}$이다.

위 행렬의 첫 행과 두 번째 행은 초점 거리와 종횡비에 따라 스케일 조정되어 시야로 들어오는 광선들이 $[-1,1]^2$ 범위로 매핑되도록 한다. 세 번째 행을 유지하는 이유는 z-buffering과 같은 가시성 연산을 수행하기 위해서는 렌더링 되는 모든 그래픽 요소에 대해 깊이 정보가 필요하기 때문이다.

만약 $z_{near}=1,z_{\text{far}} \to \infty$로 설정하고, 세 번째 행의 부호를 바꾸면, 이 스크린 벡터의 3번째 성분은 깊이의 역원이(inverse depth) 된다.

Camera intrinsics

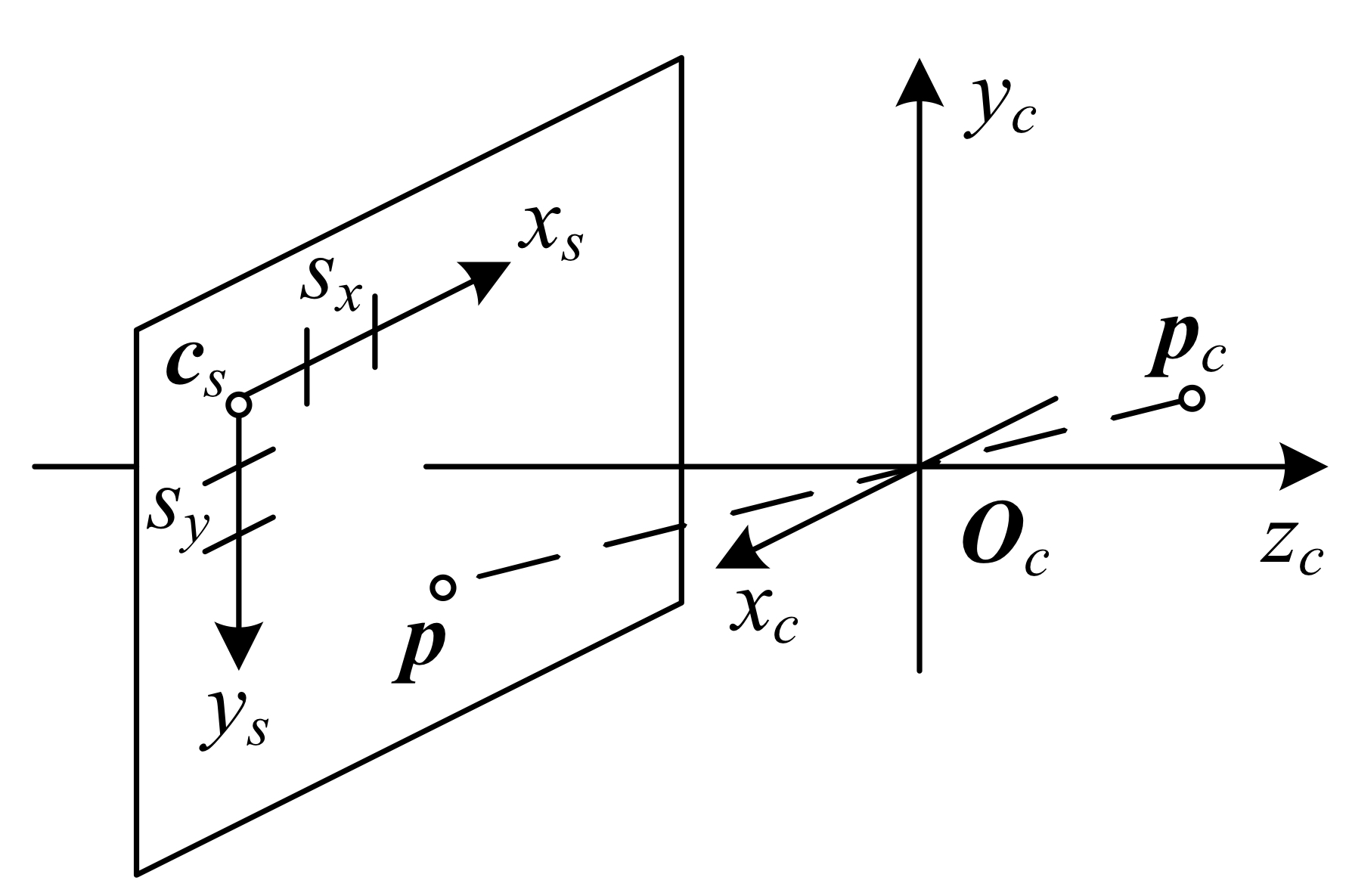
이제껏 이상적인 핀홀 모델을 통해 3차원 포인트를 투영했지만, 투영된 결과 좌표를 센서의 픽셀 간격과 센서 평면의 상대적 위치에 따라 다시 변환해야 한다. 이 변환을 위해서 첫째로 센서 호모그래피(sensor homography) 행렬 $M_s$를 사용해 2차원 픽셀 좌표에서 3차원 광선(rays)으로의 매핑을 설명하고, 둘째로, 내부 파라미터(intrinsic) 행렬 $K$와의 관계를 설명해야 한다. 이때, 내부 파라미터 행렬 $K$는 3차원 카메라 중심 좌표계의 점 $\mathbf{p}_c$를 2차원 픽셀 좌표 $\mathbf{\tilde{x}}_s$로 매핑하는데 사용한다.

이미지 센서는 정수 기반의 픽셀 좌표 $(x_s,y_s)$에 따라 픽셀 값을 반환한다. 보통 이 좌표계는 이미지의 좌상단에서 시작해 우하단으로 진행한다. 픽셀 중심을 3차원 좌표로 매핑하려면, 픽셀 간격$(s_x,s_y)$으로 스케일링한 후, 카메라 중심 $\mathbf{O}_c$에 대한 센서 배열의 방향을 센서 원점 $\mathbf{c}_s$와 3차원 회전 행렬 $\mathbf{R}_s$로 설명한다. 이런 과정을 하나의 투영 모델로 합치면 다음과 같이 표현된다.

\[\mathbf{p} = \begin{bmatrix} \mathbf{R}_s & \mathbf{c}_s \end{bmatrix} \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\0 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_s \\ y_s \\ 1 \end{bmatrix} = \mathbf{M}_s \tilde{\mathbf{x}}_s\]

이때 행렬 $\mathbf{M}_s$의 첫 두 열은 $x_s,y_s$의 방향과 대응되며, 세 번째 열은 센서 원점 $\mathbf{c}_s$이다.

행렬 $\mathbf{M}_s$는 총 8개의 미지수로 구성되는데, 회전을 설명하는 3개의 매개변수 $\mathbf{R}_s$, 이동을 설명하는 3개의 매개변수 $\mathbf{c}_s$, 2개의 스케일 펙터 $(s_x,s_y)$로 구성되어있다. (반도체 제조 기술의 발달로 이미지 평면의 두 축 간 스큐 가능성은 무시할 수 있을 정도로 작기 때문에 무시한다.) 그러나, 실제로는 센서 간격이나 방향에 대한 외부 정보가 없다면, 우리가 얻을 수 있는 자유각은 7개 뿐이다. 이미지 기반의 외부 측정만으로는 센서의 원점으로부터의 거리와 센서 스케일을 분리해낼 수 없기 때문이다.

하지만 자유도 7개를 갖는 $\mathbf{M}_s$를 직접적으로 추정하는 것은 현실적으로 불가능하기에, 대부분 일반적인 동차 $3\times3$행렬 형태를 가정한다.

3차원 픽셀 중심 $\mathbf{p}$와 카메라 기준 삼차원 포인트 $\mathbf{p}_c$사이의 관계는 미지의 스케일 계수 $s$를 통해 다음과 같이 표현된다.

\[\mathbf{p}=s\mathbf{p}_c\]

따라서 $\mathbf{p}_c, \tilde{\mathbf{x}_s}$ 간의 완전한 투영 식은 다음과 같이 쓸 수 있다.

\[\mathbf{\tilde{x}}_s=\alpha \mathbf{M}_s^{-1}\mathbf{p}_c=\mathbf{Kp}_c\]

이 $3\times3$ 행렬 $\mathbf{K}$는 캘리브레이션 행렬(calibration matrix)라고 하며, 카메라의 내부 파라미터(camera intrinsics)를 설명한다.(카메라의 공간 내 위치와 방향은 외부 파라미터(extrinsics)라고 한다.)

이론적으로 $\mathbf{K}$는 7개의 자유각을 갖지만 실제로는 $3\times3$ 동차 행렬 전체의 차원인 8개의 자유각을 갖는다. 그러나 일반적으로 $\mathbf{K}$를 상삼각 행렬로 취급하고, 자유각을 5개로 보는 이유는 외부 측정만으로는 $\mathbf{K}$의 전체 요소를 복원할 수 없기 때문이다.

외부 삼차원 점이나 측정값을 이용해 카메라 보정(Calibration)을 수행할 때, 우리는 일반적으로 내부 파라미터 $\mathbf{K}$와 외부 파라미터 $\mathbf{R,t}$를 동시에 추정하게 된다.

\[\mathbf{\tilde{x}_s=K[R \quad t]p_w = Pp_w}\]

여기서 $\mathbf{p}_w$는 알려진 삼차원 월드 좌표이며, 행렬 $\mathbf{P}$

\[\mathbf{P=K[R\|t]}\]

는 카메라 행렬(camera matrix)라고 불린다.

이 수식을 유심히 들여다보면, $\mathbf{K}$에 $\mathbf{R}_1$을 오른쪽 곱(post-multiply) 하고($\mathbf{KR_1}$), $\mathbf{[R|t]}$ 에 $\mathbf{R}_1^\top$를 왼쪽 곱(pre-multiply)을 수행($\mathbf{R_1^\top[R|t]}$)해도 유효한 보정 결과를 얻을 수 있다는 것을 알 수 있다.

종합해서 정리해보자면, 결국, 이미지 측정만으로는 센서의 실제 방향이나 진짜 카메라 내부의 파라미터를 정확히 알아내는 것은 불가능하다.

$\mathbf{K}$를 상삼각 행렬 형태로 선택하는 것이 관례적이다. 주어진 $3\times4$ 카메라 행렬 $\mathbf{P=K[R|t]}$를 $\mathbf{QR}$ 분해를 사용해 상삼각 행렬 형태의 $\mathbf{K}$를 계산할 수 있다.

상삼각 행렬 형태의 $\mathbf{K}$는 여러가지 형태로 작성할 수 있다.

첫 번째는, 센서 $x,y$축에 대해 서로 다른 초점 거리 $f_x, f_y$를 사용한 다음과 같은 표현이다.

\[\mathbf{K} = \begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}\]

$s$는 센서가 광축에 수직으로 장착되지 않아 생길 수 있는 센서 축 간의 기울기(skew)를 반영한다. $(c_x,c_y)$는 픽셀 좌표계에서 표현된 영상 중심(image center)을 나타내며, 컴퓨터 비전 분야에서는 이 영상 중심을 주점(principal point) 이라고 부르기도 한다. 반면, 광학 분야에서 주점이란 일반적으로 렌즈 내부에서 주평면이 광축과 교차하는 지점에 위치한 3차원 좌표를 의미한다.

다른 표현은 다음과 같다.

\(\mathbf{K} = \begin{bmatrix} f & s & c_x \\ 0 & af & c_y \\ 0 & 0 & 1 \end{bmatrix}\) 이때 종횡비 $a$를 명시적으로 사용하며 하나의 공통된 초점 거리 $f$를 사용한다. 반면, 실제로는 $a=1, s=0$으로 가정하여 훨씬 더 간단한 형태를 적용한다.

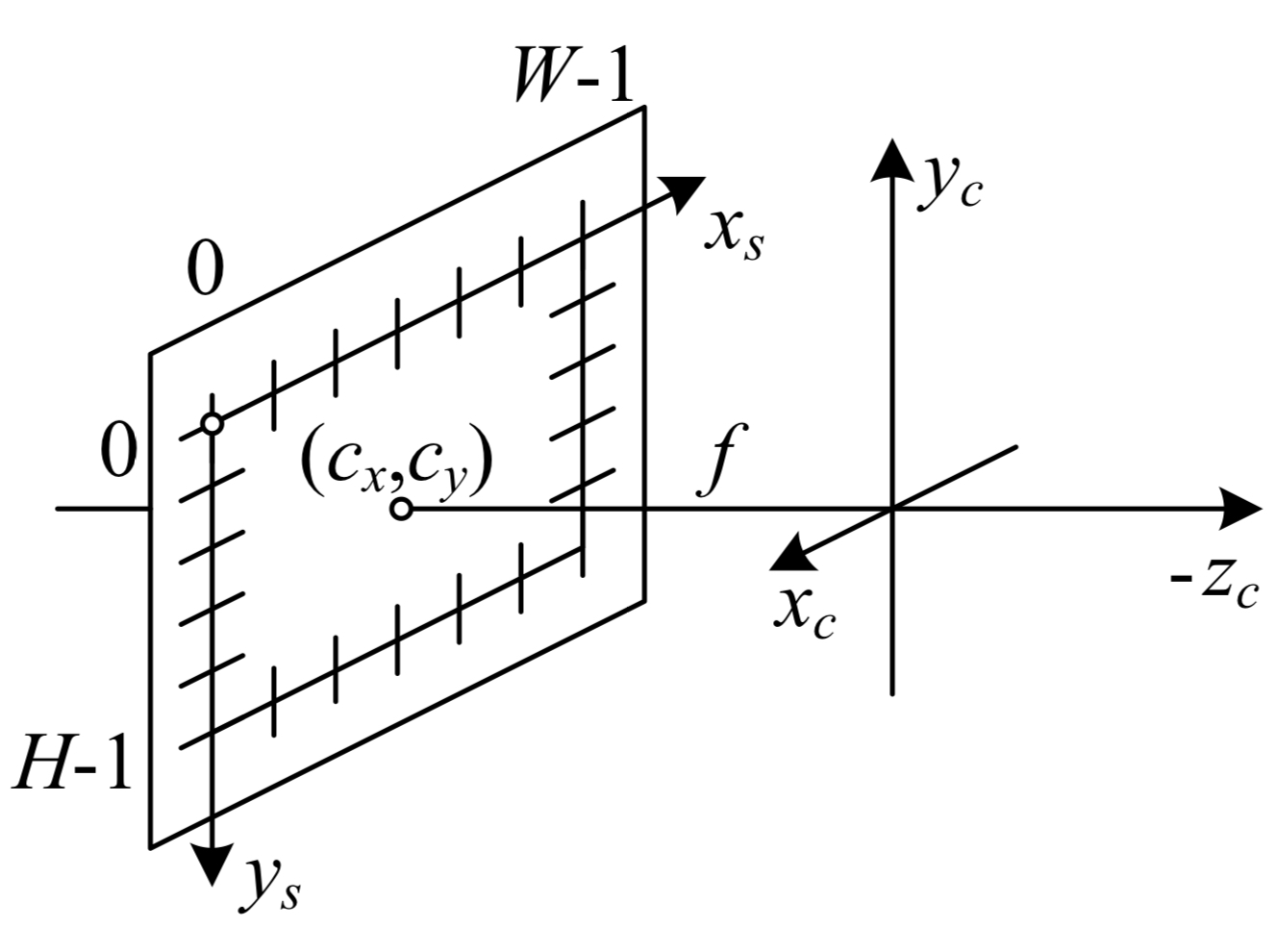
\[\mathbf{K} = \begin{bmatrix} f & 0 & c_x \\ 0 & f & c_y \\ 0 & 0 & 1 \end{bmatrix}\]

종종, 이미지의 중심을 러프하게 원점(origin)으로 두기도 한다 ($(c_x, c_y)=(W/2,H/2)$). $W,H$는 각각 너비와 높이를 의미하며, 한개의 변수를 가지고 있는 카메라 모델에 완벽히 들어맞춰 사용할 수 있다.

Figure 2.9는 단순화된 이미지 모델의 일부분으로써 이러한 값들이 어떻게 시각화되는지를 보여준다. 주목해야 할 점은 **이미지 평면을 렌즈의 결절점(투영 중심, nodal point, projection center of the lens) 앞쪽에 배치했다는 점이며, 대부분의 영상 처리 라이브러리들이 행 방향의 좌표를 처리하는 방식에 맞추기 위해 $y$축의 방향도 반전되어있다.

Focal lengths

초점 거리는 픽셀을 어떤 단위로 측정하는지에 따라 달라지기 때문에 비전 알고리즘을 구현하거나 결과를 해석할 때 종종 혼란을 야기한다. 예를 들어 픽셀 좌표를 정수값 범위 $[0,W) \times [0,H)$로 정의한다면 캘리브레이션 행렬 $\mathbf{K}$에서의 초점거리와 카메라 중심은 픽셀 단위로 표현 가능하다. 그렇다면 이 값들이 실제 사진 촬용에서 사용되는 단위의 초점 거리와는 어떻게 연결되는걸까?

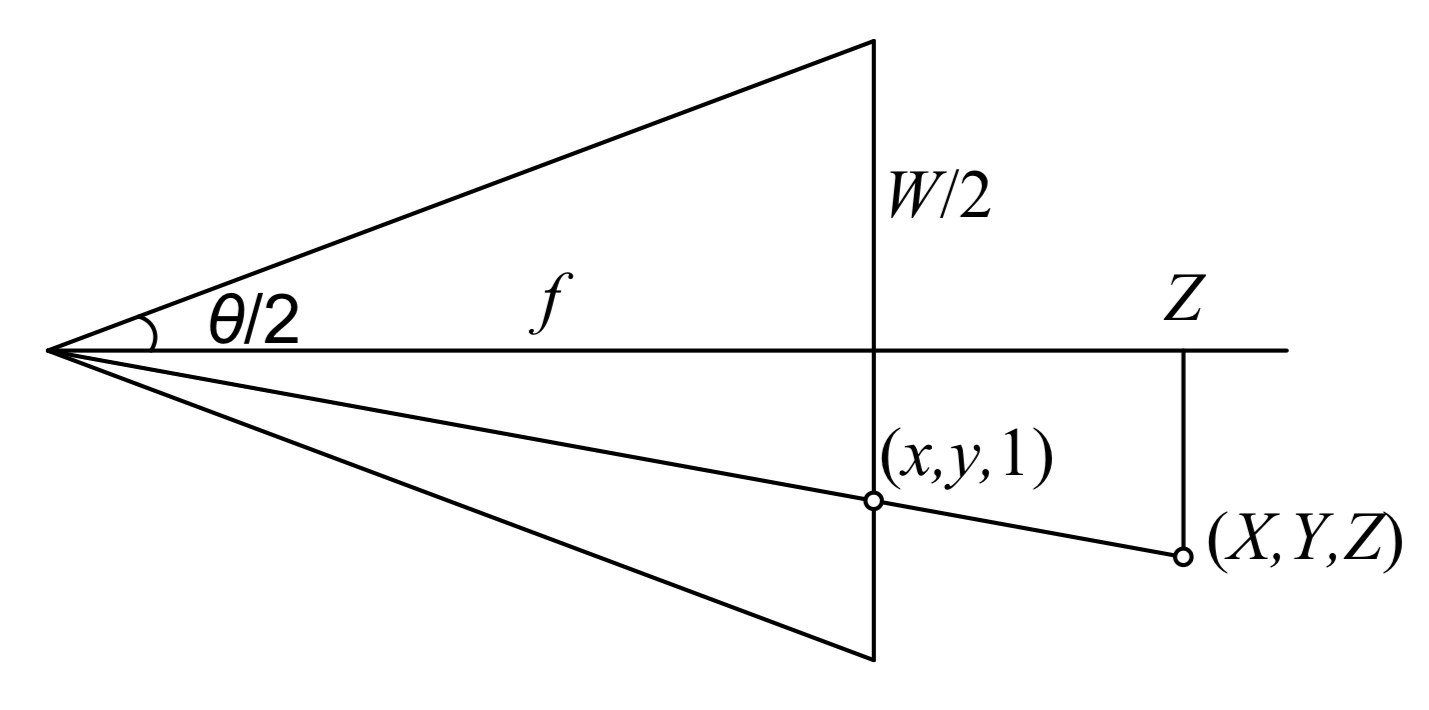
그림 2.10은 초점거리, 센서 너비, 그리고 수평 시야각 사이의 관계를 보여주며, 다음 수식을 따른다.

\[\tan{\frac{\theta_H}{2}}=\frac{W}{2f} \qquad or \qquad f=\frac{W}{2}\left[\tan{\frac{\theta_H}{2}}\right]^{-1}\]

전통적인 35mm 카메라의 노출 영역은 $24mm \times 36mm$이므로, $W=36mm$, 초점 거리 $f$도 보통 밀리미터 단위로 표현된다. 하지만 디지털 이미지 환경에서는 $W$를 픽셀 단위로 표현하고 $f$를 캘리브레이션 행렬 $\mathbf{K}$에 직접 사용할 수 있도록 하는 것이 더 편리하다.

또 다른 방식은 픽셀 좌표계를 $[-1,1)$ 범위로 정규화하는 방법도 있다. 긴 축을 $[-1,1]$, 짧은 축을 $[-a^{-1},a^{-1})$로 정규화하며, 여기서 $a \ge 1$은 이미지 종횡비(aspect ratio)를 나타낸다. 이러한 방식은 수정 정규화 디바이스 좌표 (modified normalized device coordinates)를 통해 구현할 수 있다.

\[x_s’ = \frac{2x_s - W}{S}, \quad y_s’ = \frac{2y_s - H}{S}, \qquad \text{where } \qquad S = \max(W, H)\]

이 방법의 장점은 초점거리와 카메라 중심이 이미지 해상도에 무관해지기 때문에, 다중 해상도, 이미지 피라미드 등 해상도에 따라 달라지는 알고리즘을 구현할 때 유용하다. 또한 $W$ 대신 $S = \max(W, H)$ 를 사용하면 가로 사진과 세로 사진 모두 동일한 초점 거리 표현을 사용할 수 있게 되며 만약 $S=W=2$로 설정하면, 다음과 같이 더 간단한 수식을 얻을 수 있다.

\[f^{-1}=\tan{\frac{\theta_H}{2}}\]

Camera matrix

위에서 서술한 바와 같이 카메라의 내/외부 파라미터를 함께 쓰는 $3\times4$ 카메라 행렬을 다음과 같이 표현할 수 있다.

\[\mathbf{P=K \ [R \ t]}\]

가끔은 $4\times4$ 가역 행렬을 사용하는 경우가 더 나을 때도 있으며, 이는 기존 카메라 행렬에서 마지막 행을 제거하지 않고 구성함으로써 표현할 수 있다.

\[\tilde{\mathbf{P}} = \begin{bmatrix} \mathbf{K} & 0 \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ 0^T & 1 \end{bmatrix} = \tilde{\mathbf{K}}\mathbf{E}\]

여기서 $\mathbf{E}$는 3차원 강체(Rigid-body, Euclidean) 변환이고, $\tilde{\mathbf{K}}$는 정칙(full-rank) 보정 행렬이다. 이 $4\times4$ 카메라 행렬은 3차원 세계 좌표 $\bar{\mathbf{P}}_w = (x_w, y_w, z_w, 1)$을 스크린 좌표(및 시차 __disparity__) $\mathbf{x}_s=(x_s,y_s,1,d)$로 직접 변환하는데 사용할 수 있다.

\[\mathbf{x_s\sim\tilde{P}\bar{p}_w}\]

여기서 $\sim$ 기호는 스케일에 의한 동치(equal up to scale)를 나타낸다. 즉, $\tilde{\mathbf{P}}$ 와 곱셈을 수행한 후, 결과 벡터는 그 세 번째 원소로 나누어져서 정규화된 형태 $\mathbf{x}_s = (x_s, y_s, 1, d)$ 를 얻게 된다.

Plane + parallax (projective depth)

일반적으로 $4\times3$ 카메라 행렬 $\tilde{\mathbf{P}}$을 사용할 때, 행렬의 마지막 행을 우리가 원하는 목적에 맞게 자유롭게 재정의할 수 있다. 즉, 단순히 시차를 깊이의 역수로 해석하는 전통적인 방식에만 얽매이지 않아도 된다는 의미이다.

$\tilde{\mathbf{P}}$의 마지막 행을 다음과 같이 다시 써보자.

\[\mathbf{p}_3 = s_3[\hat{\mathbf{n}}_0\|c_0]\]

이 때, $\hat{\mathbf{n}}_0$는 기준 평면의 단위 법선 벡터, $c_0$는 기준 평면의 오프셋, $s_3$는 임의의 스케일링 상수다. 이 세 변수를 통해서, 마지막 행이 하나의 평면 방정식을 암시하고 있음을 알 수 있다. 그러면 다음과 같은 수식을 얻을 수 있다.

\[d = \frac{s_3}{z} \left(\hat{\mathbf{n}}_0 \cdot \mathbf{p}_w + c_0\right)\]

이 때, $d$는 시차 또는 투영 깊이를 의미하며, $\mathbf{P}_w$는 삼차원 공간 상의 점, $\hat{\mathbf{n}}_0\cdot\mathbf{p}_w + c_0 = 0$은 기준 평면의 일반형이다. 위 수식은 삼차원 점이 기준 평면으로부터 얼마나 떨어져 있는지를 투영 형태로 해석하는 방식이다. 또한, 점이 카메라 중심 $C$로부터 광축(z축) 방향으로 얼마나 떨어져 있는지 나타내기 위해 다음 수식을 사용할 수 있다.

\[z=\mathbf{r}_z\cdot(\mathbf{P}_w-c)\]

즉, $z$는 삼차원 상의 점을 카메라 Z축 방향 단위 벡터 $\mathbf{r}_z$와 내적하여 계산한 거리이다. 따라서 시차 $d$는 단순한 깊이의 역이 아닌, 기준 평면으로부터의 투영 거리로 해석될 수 있다. 기준 평면이 $\mathbf{\hat{n}_0\cdot p_w}+c_0=0$일 때, 삼차원 점이 평면으로부터 얼마나 떨어져 있는지를 나타낸다.

만약, 기준 평면이 무한대에 위치한다고 가정하면 $\mathbf{\hat{n}}_0 = 0, c_0 = 1$이 되며, 이때, 표준적인 시차 $d=\frac{s_3}{z}=\frac{1}{z}$(깊이의 역)를 얻을 수 있다.

이러한 구조를 이해하는 또 다른 방법은, $\tilde{P}$ 행렬을 역행렬로 만들어서, 픽셀 좌표와 시차가 포함된 벡터 $\mathbf{x}_s$로부터 직점 삼차원 점을 복원하는 방식이다.

\[\mathbf{\tilde{p}_w=\tilde{P}^{-1}x_s}\]

• $\mathbf{x}_s = (x_s, y_s, 1, d)^T$: 픽셀 좌표 + 시차 정보 포함
• $\tilde{\mathbf{P}}^{-1}$: $4\times4$ 정칙 행렬이므로 역변환 가능

일반적으로 $\tilde{P}$를 목적에 따라 주유롭게 구성해 공간을 임의의 투영 방식으로 샘플링하는데 사용할 수 있다. 이러한 접근은 다중 시점 스테레오 재구성 알고리즘(multi-view stereo reconstruction)을 구성할 때 특히나 유용한데, 왜냐하면, 여러 개의 평면을 공간 속에서 ‘쓸어가며’(plane sweeping) 이미지의 움직임에 가장 잘 맞는 방식으로 가변적 샘플링을 할 수 있기 때문이다.

Mapping from one camera to another

3차원 공간의 상을 서로 다른 위치의 카메라로 촬영하게 되면 어떤 일이 일어날까? 풀 랭크의 $4\times4$ 카메라 행렬 $\mathbf{\tilde{P}=\tilde{K}E}$를 활용해 3차원 월드 좌표계를 스크린 좌표계로 다음과 같이 투영할 수 있다.

\[\tilde{\mathbf{x}}_0 \sim \tilde{\mathbf{K}}_0 \mathbf{E}_0 \mathbf{p} = \tilde{\mathbf{P}}_0 \mathbf{p}\]

이때 한 이미지의 픽셀에 대해 z-buffer나 시차 값 $d_0$를 알고있다면 삼차원 점의 위치 $\mathbf{p}$를 다음과 같이 계산할 수 있다.

\[\mathbf{p \sim E_0^{-1}\tilde{K}_0^{-1}\tilde{x}_0}\]

그리고 이를 다른 이미지로 투영하면 다음과 같다.

\[\tilde{\mathbf{x}}_1 \sim \mathbf{K}_1 \mathbf{E}_1 \mathbf{E}_0^{-1} \tilde{\mathbf{K}}_0^{-1} \tilde{\mathbf{x}}_0 = \mathbf{M}_{10} \tilde{\mathbf{x}}_0\]

그러나 일반적으로 사진 이미지에서 픽셀의 깊이 좌표값을 얻어내기는 힘들다. 그러나 장면이 평면일 경우 $z=\mathbf{r}_z\cdot(\mathbf{P}_w-c)$ 수식을 사용하여 $\mathbf{P}_0$의 마지막 행을 일반적인 평면 방정식 $\mathbf{\hat{n}_0\cdot p} + c_0$로 대체하여, 이 평면상의 점들이 $d_0=0$인 값으로 매핑되도록 할 수 있다. 따라서 $d_0=0$으로 설정하면 상단의 수식에서 마지막 열과 행을 무시할 수 있고 투영 식을 다음처럼 단순화 할 수 있다.

\[\tilde{\mathbf{x}}_1 \sim \tilde{\mathbf{H}}_{10} \tilde{\mathbf{x}}_0\]

이 때, $\mathbf{\tilde{H}_{10}}$은 $3\times3$ 동차 행렬이며, $\tilde{\mathbf{x}}_n$은 2차원 동차 좌표이다.

깊이를 몰라도 카메라 간 매핑이 가능한 또 다른 경우는, 카메라가 ‘순수 회전’만 수행하는 경우이며, 이 경우 다음과 같이 $3\times 3$ 동차 행렬로 쓸 수 있다.

\[\tilde{\mathbf{x}}_1 \sim \mathbf{K}_1 \mathbf{R}_1 \mathbf{R}_0^{-1} \mathbf{K}_0^{-1} \tilde{\mathbf{x}}_0 = \mathbf{K_1R_{10}K_0^{-1}\tilde{x}_0}\]

이 수식이 의미하는 바는 내부 보정 행렬이 주점과 종횡비를 알고 있다고 가정하면, 이 호모그래피는 회전량과 두 초점 거리로 매개변수화 할 수 있다는 것이다.

Object-centered projection

긴 초점 거리 렌즈를 사용할 때에는 초점 거리와 객체까지의 거리가 강한 연관성을 가져 이 둘의 영향을 구분하기 어렵기에 이미지 측정값만으로 초점 거리를 신뢰성 있게 추정하기 어려운 경우가 자주 발생한다. 이런 애매모호함은 다음과 같이 투영식을 정리하면 좀 더 명확해진다.

\[x_s = f\frac{ \mathbf{r}_x \cdot \mathbf{p} + t_x}{\mathbf{r}_z \cdot \mathbf{p} + t_z} + c_x\] \[y_s = f\frac{\mathbf{r}_y \cdot \mathbf{p} + t_y}{\mathbf{r}_z \cdot \mathbf{p} + t_z} + c_y\]

이 때 $\mathbf{r_x,r_y,r_z}$는 행렬 $\mathbf{R}$의 세 개 행을 의미한다.

만약 객체까지의 거리 $t_z$가 매우 크다면, 분모는 거의 $t_z$로 근사되고, 결과적으로 투영된 객체의 크기는 $f/t_z$의 비율에 의해 결정되며, 다음과 같은 변수 치환을 통해 수식을 다시 정리할 수 있다.

\[\eta_z = \frac{1}{t_z}, \quad s = \eta_z f\] \[x_s = \frac{s\, \mathbf{r}_x \cdot \mathbf{p} + t_x}{1 + \eta_z \mathbf{r}_z \cdot \mathbf{p}} + c_x\] \[y_s = \frac{s\, \mathbf{r}_y \cdot \mathbf{p} + t_y}{1 + \eta_z \mathbf{r}_z \cdot \mathbf{p}} + c_y\]

이 때 투영 스케일$s$는 삼차원 좌표 $\mathbf{p}$를 알고 있는 객체를 볼 때 신뢰성 있게 추정할 수 있으며, 역거리 $\eta_z$는 스케일$s$의 추정과 거의 독립적이고, 객체가 회전할 때 생기는 원근 왜곡의 양으로부터 추정할 수 있다. 따라서, 원근 투영 모델을 굳이 정사영 모델로 바꿀 필요 없이 동일한 식을 그대로 사용할 수 있다.

Lens distortions

상술한 영상 모델들은 카메라가 선형 투영 모델을 따른다고 가정하며, 실제 세계의 직선이 이미지에서도 직선으로 보인다고 가정한다. 하지만, 대부분의 광각 렌즈에서는 반지름 방향의 왜곡(radial distortion)이 일반적으로 발생하며, 직선이 곡선처럼 휘어 보이게 된다. 이 왜곡을 보정하지 않으면, 정확한 포토리얼리스틱 복원은 불가능하다.

다행히도 반지름 방향의 왜곡을 보정하는건 그다지 어렵지 않다. 대부분의 렌즈에 대해서 4차 다항식 기반의 단순 모델로도 실용적 보정이 가능하다 $(x_c,y_c)$를 투영된 좌표에서 초점 거리 스케일링과 중심 이동 전에 얻는 값이라고 해보자.

\[x_c = \frac{\mathbf{r}_x \cdot \mathbf{p} + t_x}{\mathbf{r}_z \cdot \mathbf{p} + t_z}\] \[\quad y_c = \frac{\mathbf{r}_y \cdot \mathbf{p} + t_y}{\mathbf{r}_z \cdot \mathbf{p} + t_z}\]

위 수식을 거치면 왜곡된 좌표는 중심을 기준으로 바깥(배럴 왜곡, barrel distortion, Figure 2.13a) 또는 안쪽(핀쿠션 왜곡, pincushion distortion, Figure 2.13b)으로 밀려나며, 이 밀림의 크기는 중심에서의 거리 $r_c$에 비례한다. 이때, 저차원 다항식을 사용한 반지름 방향의 왜곡 모델은 다음과 같다.

\[\hat{x}_c = x_c (1 + \kappa_1 r_c^2 + \kappa_2 r_c^4), \ \hat{y}_c = y_c (1 + \kappa_1 r_c^2 + \kappa_2 r_c^4) \qquad \quad r_c^2 = x_c^2 + y_c^2\]

여기서 $\kappa_1, \kappa_2$는 반지름 왜곡 계수(radial distrotion parameters)이다. 이 모델에는 비대칭 렌즈 배치를 보정하기 위한 접선 성분(tangentail component)도 있으나, 불안정한 추정치를 유발하기에 일반적으로는 무시하며, 최종적인 왜곡 보정 후의 픽셀 좌표는 다음과 같이 계산된다.

\[x_s = f \hat{x}_c + c_x, \quad y_s = f \hat{y}_c + c_y\]

어안 렌즈(fisheye lens)는 여태까지 설명한 전통적인 다항식 기반 왜곡 모델과는 다른 접근이 필요하다. 어안렌즈는 광축에서 떨어진 각도 $\theta$에 대해 등거리(equi-distance) 투영을 수행한다고 볼 수 있는데, 이는 극좌표 투영과 동일한 수식이다.

\[r=f\theta\]

이러한 렌즈는 f-세타 렌즈라고도 불리며, 왜곡이 더 크거나 불규칙할 경우, 스플라인 기반의 파라메트릭 모델이 필요할 수 있으며, 투영 중심이 일정하지 않은 렌즈는 픽셀마다 3차원 선을 별도로 모델링해야 할 수 있다.