Dimensionality Reduction
차원 축소
차원 축소란 고차원의 데이터를 포함하는 핵심 정보와 패턴을 유지하는 동시에 더 낮은 차원의 공간으로 표현하는 과정이다. 차원 축소는 데이터 분석, 시각화 및 모델링을 용이하게 하며, 고차원 데이터셋에서는 계산 효율성을 높이고, 과적합을 방지하는데 도움이 된다. 더불어, 차원 축소는 데이터의 중요한 특성을 보다 명확히 드러내여, 더 효과적인 인사이트와 결론 도출에 기여한다.
PCA(주성분 분석)
PCA(주성분 분석)는 고차원의 데이터를 저차원으로 축소하는 통계적 기법이다.
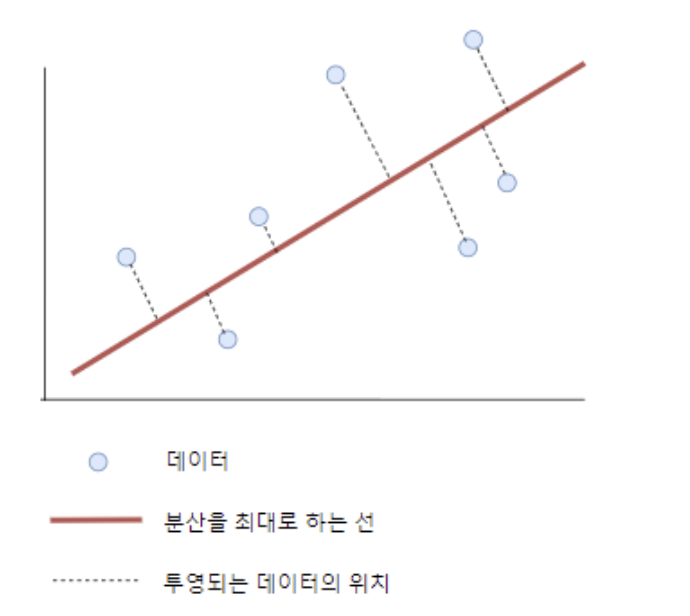
PCA는 데이터의 분산을 최대화하는 방향으로 새로운 축을 찾아, 데이터를 이 축에 투영한다.
2차원일 때는 그림과 같이 첫 번째 주성분(실선)은 데이터가 가장 넓게 퍼져있는 방향을 나타내며, 두 번째 주성분은 첫 번째 주성분에 직교하는 방향으로 설정된다.
3차원 이상일 때, 첫 번째 주성분은 동일한 역할을 하지만, 두 번째 주성분은 첫 번째 주성분에 직교하는 방향 중 가장 큰 분산을 설명하고, 세 번째 주성분은 이전 두 주성분에 모두 직교하며 남은 분산을 포착한다.
PCA의 장단점
| 장점 | 단점 |
|---|---|
| 데이터의 특성을 유지하며 차원을 줄이고 복잡성 감소 | 주성분은 원본 변수들의 선형 결합으로 구성되어 무엇을 의미하는지 해석하기 어려움 |
| 불필요한 변동성을 제거하여 데이터의 핵심 특성을 더욱 명확히 함 | 차원을 줄이는 과정에서 일부 정보 손실 가능성 |
| 저차원으로 변환된 데이터는 시각화와 해석 용이 | 모든 변수의 동일한 중요도를 가정하므로 어떤 변수가 더 중요한지 구별하기 어려움 |
| 데이터 처리와 분석이 더 빠르고 효율적 |
결측치가 있는 경우 데이터의 분산을 올바르게 파악할 수 없으며, 주성분이 잘못 계산될 수 있다. 또한 데이터의 각 특성이 서로 다른 스케일을 가질 경우, 스케일이 큰 특성이 결과에 더 큰 영향을 미치게 된다.
따라서 PCA 이전에 스케일링을 수행하는 것은 중요한 이점을 가진다. 또한, 스케일링 과정에서 각 특성의 평균을 0으로 조정하기 때문에, 전체 데이터에서 평균을 빼는 중심화 과정을 거치지 않게 되어 PCA과정이 간소화 된다.
PCA 구현 1 : 특잇값 분해
PCA를 수행하는 데에는 주로 다음 두 가지 방법을 사용한다.
- 고윳값 및 고유 벡터를 사용
- Singular Value Decomposition(SVD)
이 때 SVD를 주로 사용하여 PCA를 구현하는 이유는 다음과 같다.
- SVD는 고유값 분해에 비해 수치적으로 더 안정적이며, 고차원 데이터나 특이값이 매우 작은 경우에 이점이 있다.
- SVD는 고차원 데이터에 대해서도 효율적으로 작동하며, 분산이 낮은 주성분을 빠르게 제거할 수 있다.
$\mathsf{A}$ : 우리가 분해하고자 하는 원본 데이터를 나타내는 행렬 (m x n)
$\mathsf{U}$ : 좌측 특이 벡터들을 담고 있는 행렬. 원본 데이터의 행과 관련된 변환을 나타낸다. (m x m)
$\mathsf{\Sigma}$ : 특이값들이 대각선에 위치하는 대각 행렬. 데이터의 각 축에 대한 분산을 나타낸다. (n x m)
$\mathsf{V^T}$ : 우측 특이 벡터들의 전치 행렬로, 원본 데이터의 특성(열)과 관련된 정보를 담고 있다. (n x n)
SVD를 사용한 PCA에서는 $\mathsf{V^T}$만 주성분 분석에 사용된다.
1
2
3
4
import numpy as np
U, S, Vt = np.linalg.svd(scaled_train, full_matrices = False)
#full_matries = False 파라미터를 통해 계산 비용을 절약할 수 있다.
PCA 구현 2 : 주성분 선택
1
2
3
4
5
6
7
#주성분 개수 설정
n_components = 3
#n_components에 해당하는 주성분만 선택
components_train = Vt[:n_components]
components_train.shape
상술한 $\mathsf{V^T}$는 SVD를 통해 얻은 우측 특이 벡터들의 전치 행렬로, 이 행렬의 각 행은 원본 데이터의 특성들을 새로운 축(주성분)으로 변환하는 역할을 한다.
코드에서는 데이터의 가장 중요한 정보를 포착하는 상위 3개의 주성분을 선택하고 있다. 이 주성분들은 데이터의 분산을 최대화하는 방향으로 정렬되어 있으며, 이를 통해 데이터의 차원을 축소하면서도 중요 정보를 유지할 수 있다.
선택된 주성분(components_train)은 이후 데이터를 이 새로운 축에 투영하는데 사용되며, 이는 저차원으로 효과적으로 축소하면서도 데이터의 핵심적인 변동성을 유지할 수 있게 해준다.
PCA 구현 3 : 데이터 투영
\(\mathsf{Scaled\_Data \ x \ (Components\_train)^T = PCA\_train}\) 데이터를 주성분에 투영하기 위해 각 데이터 포인트를 주성분의 방향으로 투영한다. 이는 데이터의 차원을 축소하고, 주성분이 포착하는 변동성을 기반으로 데이터를 재구성한다.
1
2
3
4
5
#학습 데이터를 주성분에 투영
pca_train = np.dot(scaled_train, components_train.T)
#테스트 데이터를 주성분에 투영
pca_test = np.dot(scaled_test, components_train.T)
LDA(선형 판별 분석)
PCA와 마찬가지로 LDA 또한 고차원 데이터를 저차원으로 축소하는 데 사용되는 기법으로, 주로 분류 문제에서 데이터의 클래스를 가장 잘 구분할 수 있는 축을 찾는데 초점을 맞춘다. LDA는 클래스 간 분산은 최대화하되, 클래스 내 분산은 최소화하는 방식으로 작동한다.
LDA는 데이터 내에 존재하는 클래스 간의 차이를 명확히 하여 데이터의 시각화 및 해석을 용이하게 하며, 데이터의 복잡성을 감소시킨다.
LDA를 활용한 데이터 차원 축소 및 변환
LDA는 분류 문제를 위해 설계된 지도학습 기법이다. LDA의 주 목적은 클래스 간 구분을 최대화 하는 동시에 클래스 내 분산을 최소화하는 특성 축을 찾아 다차원 데이터를 저차원으로 효과적으로 축소하여 계산 효율성을 높인다.
LDA는 각 클래스의 데이터를 가장 잘 구분하는 선형 결합을 찾아내며, 이는 분류를 위한 결정 경계를 설정하는 역할을 한다. PCA와는 달리 LDA는 각 클래스에 속한 데이터 포인트의 레이블 정보를 활용하여 분류 성능을 극대화 하는 특성 축을 찾는다.
PCA와의 차이점을 정리하자면 PCA는 데이터의 주요 변동성을 강조하는 데 유용한 반면, LDA는 분류 작업에서 높은 성능을 발휘한다.
| 장점 | 단점 |
|---|---|
| 데이터의 클래스별 평균 차이가 클 때 탁월한 성능 발휘 | 클래스 불균형, 비정규 분포, 다중 공선성과 같은 데이터의 특정한 특성에 의해 성능 영향 |
| 차원 축소 시 클래스 간 거리 고려로인해 생성된 축은 해석 용이성이 높음 | 클래스 수에 따라 생성할 수 있는 성분 수 제한 |
| 분산 구조가 일정한 가정이 위반되더라도 비교적 잘 작동 | 데이터가 정규분포를 따른다고 가정하므로, 가정에서 벗어날 경우 성능 저하 유발 |
1
2
3
4
5
6
7
8
9
10
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA()
lda.fit(scaled_train, y_train)
lda_transformed_train = lda.transform(scaled_train)
lda_columns = [f'lda{i+1}' for i in range(lda_transformed_train.shape[1])]
lda_df = pd.DataFrame(lda_transformed_train, columns = lda_columns)
LDA 파라미터
- solver
- svd : Singular Value Decomposition, 계산 효율성이 높고 특성 선택에 영향을 받지 않으며, 추가적인 공분산 계산이 필요 없다.
- lsqr : 최소 제곱 해를 찾는 알고리즘 사용
- eigen : 고유값 분해를 사용하여 공분산 행렬을 계산
- shrinkage : lsqr과 eigen에서 사용되며, 공분산 추정에 대한 정규화를 적용한다. 주로 샘플 수보다 특성이 많은 경우에 유용하다.
- priors : 클래스별 사전 확률을 지정한다.
- n_components : 축소할 차원의 수를 지정하며, 기본값은 클래스의 수 - 1중 더 작은 값으로 설정된다.
- tol : 수치적 안정성을 위한 공분산 행렬의 절단 기준값이다. svd에서는 사용되지 않는다.
구성 요소별 설명된 분산 비율 시각화
데이터의 고차원성은 차원의 저주문제를 야기시키며, 차원이 증가함에 따라 같은 수의 데이터 포인트들 사이의 거리가 점점 멀어진다.
이는 데이터의 밀도가 감소함을 의미하며, 데이터 포인트들 간의 상대적 거리가 증가하는 결과를 가져온다. 고차원 데이터셋에서는 이 거리의 증가가 더욱 극적으로 나타나며, 데이터 분석에 상당한 문제점이 된다.
결과적으로, 모델이 더 많은 데이터를 요구하며, 모델의 성능 저하와 과적합 발생의 위험성을 가지게 된다.
이에 대한 해결책으로 Scree Plot과 같은 도구를 사용하여 차원 축소 시의 최적 차원 수를 결정할 수 있다.
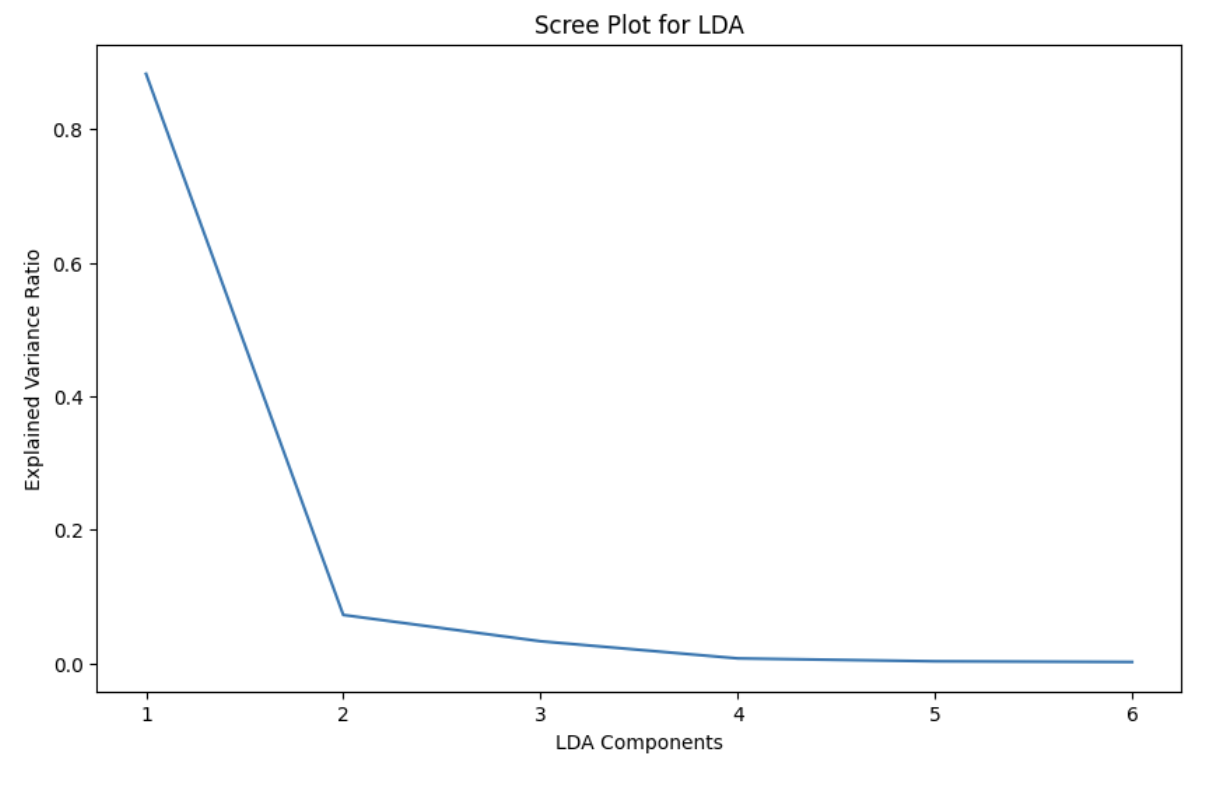
설명된 분산의 증가율이 급격히 감소하는 지점과 그 이후 분산 감소가 완만해지는 부분을 찾아, 그 지점 이후의 주성분은 덜 중요하다고 판단한다.
일반적으로 차원 축소된 차원의 설명된 분산 비율을 70%에서 90% 사이를 목표로 설정하고, 이러한 지점을 elobw라고 부른다.
1
2
3
4
5
6
plt.figure(figsize=(10, 6))
plt.plot(range(1, lda_transformed_train.shape[1] + 1), lda.explained_variance_ratio_)
plt.xlabel('LDA Components')
plt.ylabel('Explained Variance Ratio')
plt.title('Scree Plot for LDA')
plt.show()
PCA를 이용한 분산 설명률 및 구성 요소 시각화
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.decomposition import PCA
# PCA 객체 생성
pca = PCA()
# 훈련 데이터에 PCA 적용
pca.fit(scaled_train)
pca_transformed_train = pca.transform(scaled_train)
# Scree Plot 그리기
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(pca.explained_variance_ratio_) + 1), pca.explained_variance_ratio_, marker='o')
plt.title('Scree Plot for PCA')
plt.xlabel('Number of Components')
plt.ylabel('Explained Variance Ratio')
plt.xticks(range(1, len(pca.explained_variance_ratio_) + 1)) # X축 눈금 설정
plt.show()
위 코드는 PCA를 이용해 데이터의 차원을 축소하는 과정과, 적절한 차원의 수를 결정하기 위한 Scree Plot을 그리는 과정을 나타낸다. LDA를 수행한 후와 마찬가지로 각 주성분이 데이터의 분산에 기여하는 정도를 보여주며, 이 과정을 통해 찾아낸 적절한 차원의 수는 다음 스텝에서 PCA를 재정의하고, 학습 데이털르 다시 변환하는 데 사용된다.
지정된 차원 수로 LDA와 PCA 재적용
마지막으로 정리하자면 LDA는 지도 학습 방식의 차원 축소 기법으로, 데이터의 클래스 레이블을 활용해 클래스 간 분리를 최대화하는 방식으로 작동한다. 반면, PCA는 비지도 학습 방식의 축소 기법으로, 데이터 분산을 최대화하는 주성분을 찾는것을 목표로 한다.
이러한 차이점을 고려할 때, LDA와 PCA는 서로 다른 유형의 문제와 데이터셋에 적합하다. 공통점은 이러한 차원 축소된 데이터는 원래 데이터프레임에 결합될 수 있으며, 이는 축소된 특성과 원래 데이터의 다른 특성들을 함께 활용하여 더 풍부한 데이터 분석을 가능하게 한다.
1
2
3
4
5
6
7
8
9
10
11
# LDA, PCA 객체 재생성
lda = LDA(n_components=2)
pca = PCA(n_components=4)
# LDA, PCA를 훈련 데이터에 적용
lda.fit(scaled_train, y_train)
pca.fit(scaled_train)
# 차원 축소가 완료된 각 데이터
lda_transformed_train = lda.transform(scaled_train)
pca_transformed_train = pca.transform(scaled_train)
3D 시각화
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(20, 10))
# LDA 3D 시각화 (가상의 3번째 축 추가)
# 3D로 표현하기 위해 projection='3d'를 지정합니다.
ax = fig.add_subplot(1, 2, 1, projection='3d')
# LDA 변환된 데이터를 3D 스캐터 플롯으로 시각화합니다. 여기서는 LDA가 2차원 데이터이므로, 세 번째 축은 0으로 설정하여 가상의 축을 추가합니다.
scatter = ax.scatter(xs = lda_transformed_train[:, 0], ys = lda_transformed_train[:, 1], zs = np.zeros_like(lda_transformed_train[:, 0]), c = y_train, cmap = plt.cm.rainbow)
ax.set_title('LDA: 2D Projection with Zero Third Dimension')
ax.set_xlabel('LDA Component 1')
ax.set_ylabel('LDA Component 2')
ax.set_zlabel('Zero Axis')
# PCA 3D 시각화 (처음 세 주성분 사용)
ax = fig.add_subplot(1, 2, 2, projection='3d')
# 두 번째 서브플롯을 생성할 때, PCA 변환된 데이터의 처음 세 주성분을 사용하여 3D 스캐터 플롯으로 시각화합니다.
scatter = ax.scatter(xs = pca_transformed_train[:, 0], ys = pca_transformed_train[:, 1], zs = pca_transformed_train[:, 2], c = y_train, cmap = plt.cm.rainbow)
ax.set_title('PCA: First 3 Components')
ax.set_xlabel('PCA Component 1')
ax.set_ylabel('PCA Component 2')
ax.set_zlabel('PCA Component 3')
legend = ax.legend(*scatter.legend_elements(), title="Classes")
ax.add_artist(legend)
plt.show()
위 코드는 LDA와 PCA를 이용하여 차원 축소된 데이터를 3차원 공간에서 시각화하는 방법을 보여준다.
위에서 LDA로 처리된 데이터는 2차원이다. 따라서, 데이터에 가상의 세 번째 축을 추가해 3차원 공간에 표현하였다. PCA로 처리된 데이터는 4차원이기에 데이터의 분산을 최대화 하는 주성분을 순서대로 찾는다. 따라서 첫 세 개의 주성분만으로 전체 데이터의 60%를 설명할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 2차원 시각화
plt.figure(figsize=(16, 8))
# LDA 변환 결과 시각화
plt.subplot(1, 2, 1)
sns.scatterplot(x=lda_transformed_train[:, 0], y=lda_transformed_train[:, 1], hue=y_train, palette=plt.cm.rainbow)
plt.title('2D Projection from LDA')
plt.xlabel('LDA Component 1')
plt.ylabel('LDA Component 2')
# PCA 변환 결과 시각화 (처음 두 주성분 사용)
plt.subplot(1, 2, 2)
sns.scatterplot(x=pca_transformed_train[:, 0], y=pca_transformed_train[:, 1], hue=y_train, palette=plt.cm.rainbow)
plt.title('2D Projection from PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
# 시각화 결과를 표시합니다.
plt.show()
Enjoy Reading This Article?
Here are some more articles you might like to read next: