용어 정리

디지털 이미지 센서의 성능에 영향을 미치는 주요 요인들로는 셔터 스피드, 샘플링 피치, 체움 계수(충전율), 센서 크기(Chip size), 아날로그 게인(Analog gain), 센서 노이즈 및 아날로그-디지털 변환기의 해상도 및 품질을 들 수 있다.

Shutter Speed

셔터 스피드(Shutter Speed)는 이미지 센서가 빛에 노출되는 시간의 길이로 정의할 수 있다. 셔터 스피드가 길수록 더 많은 빛이 센서에 들어오고, 짧을수록 적은 빛만 들어온다.

조도 조절 : 센서에 도달하는 빛의 양을 조절하여 결과적으로 이미지가 Under/Over-exposed 되는 것을 결정한다.
모션 블러 : 움직이는 대상이 촬영되는 동안 셔터가 열려 있으면, 움직임이 번져 보이는 현상이 발생한다. 셔터 속도가 빠를수록 움직임이 정지된 것 처럼 보이고, 느릴수록 흐릿해진다.

Fill Factor

이론적 감지 면적 대비 실제 감지 면적의 비율

충전율은 센서의 셀에서 실제로 빛을 감지하는 활성 면적 비율을 의미한다.

\[\frac{(\text{Active sensing area})}{(\text{Total available area})}\]

충전율이 높을수록 더 많은 빛을 수집 가능하며 얼라이어싱(Aliasing)이 감소한다. 충전율은 일반적으로 캘리브레이션 장비를 통해 실험적으로 측정이 가능하다.

요약하면, 충전율이 높을수록 감도와 성능은 오르고 왜곡은 줄어든다.

Sampling Pitch

센서의 셀 사이의 물리적 간격

샘플링 피치는 이미지 센서에서 인접한 픽셀 간의 거리를 의미한다.

샘플링 피치가 작을수록 샘플링 밀도(Sampling Density)가 증가하여 해상도가 증가하지만, 각 센서의 면적이 감소해 받아들이는 빛(광자, Photon)의 수가 감소하여 노이즈가 증가하고 저조도에서의 성능이 저하된다

요약하자면 샘플링 피치가 낮아지면 해상도와 노이즈는 오르며 감도는 낮아진다.

Chip Size

센서 전체 면적

칩의 크기는 이미지 센서가 차지하는 물리적 칩의 크기이며 인치 단위로 표현된다. 크면 클수록 픽셀당 면적이 증가하여 광 감도가 증가하지만 그에 상응하는 제작 비용이 수반된다.

Analog Gain

센서 신호의 증폭량

아날로그 게인은 아날로그-디지털 변환 전에 센서에서 감지한 미약한 신호를 증폭시키는 과정이며, 주로 sense amplifier를 통해 수행된다.

일반적인 비디오 카메라는 Automatic Gain Control(AGC)로 자동 조절되며, 디지털 카메라는 사용자가 ISO설정을 통해 수동으로 조절할 수 있다.

Sensor Noise

이미지 센싱 과정에서 발생하는 다양한 형태의 신호 왜곡

노이즈는 빛의 세기, 노출 시간, 센서 게인을 통해 그 수준이 결정된다. 또한 픽셀 밝기에 따른 노이즈 분산 모델(Noise Level Function, NLF)을 구할 수 있으며, 사전 캘리브레이션이나 반복 촬영으로 추정이 가능하다.

노이즈의 추정은 영상 복원, 테두리 검출, 정합 등에 중요하게 사용되며 일정한 밝기의 영역에서 노이즈 분산을 추정하는것이 가장 단순한 형태이다.

종류

Fixed pattern noise: 정해진 위치에서 반복되는 패턴 노이즈
Dark current noise: 빛이 없을 때도 발생하는 전류 노이즈
Shot noise: 광자 수의 확률적 변화에 따른 노이즈
Amplifier noise: 신호 증폭기에서 유입되는 노이즈
Quantization noise: ADC 변환 중 발생하는 근사화 오차

ADC Resolution

아날로그 신호를 디지털 비트로 변환하는 정밀도

ADC 해상도는 센서에서 수집한 아날로그 신호를 디지털 값으로 변환하는 최종 단계이다.

Resolution : 몇 비트로 표현하느냐(8-bit JPEG, 12_16 bit RAW, etc…)
Noise Level : 변환된 비트 중 실제로 유효하게 사용 가능한 비트 수

센서 노이즈와 유사하게 동일 장면을 반복 촬영하고 밝기에 따른 노이즈를 측정해 유효 비트를 추정하여 확인할 수 있다.

Digital Post-Processing

센서에서 디지털로 변환된 데이터의 이미지 개선 작업

디지털 후처리는 변환된 픽셀 값을 저장하기 전에 이미지 품질을 향상시키기 위한 작업들을 통들어 일컫는다.

주요 작업 항목은 다음과 같다.

CFA Demosaicing: 컬러 필터 배열의 픽셀을 보간하여 RGB 이미지 재구성
White Point Setting: 백색 균형 조정
Gamma Mapping: 감마 함수로 동적 범위 향상

Sampling and aliasing

Figure 2.15 1차원 신호의 얼라이어싱 : 파란 사인파와 붉은 사인파는 샘플링 주파수 f=2에서 동일한 디지털 샘플을 갖는다. 필 팩터가 100%인 박스 필터로 컨볼루션 한 이후에도, 두 신호는 크기는 다르지만 여전히 얼라이어싱 상태에 있다. 이는 샘플링된 붉은 신호가 파란 신호를 반전시키고 크기를 줄인 형태처럼 보이기 때문이다.

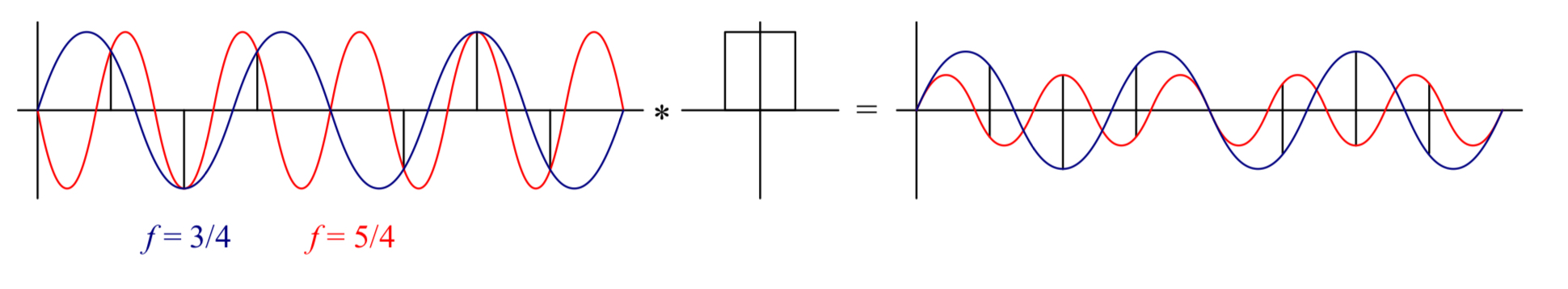
이미지 센서에 입사하는 빛의 장(field of light)이 영상 칩의 활성 감지 영역(active sense areas)에 떨어지면 각 활성 셀에 도달한 광자들은 통합(integrated)된 후 디지털화된다. 그러나 칩 위의 충전율이 작고, 신호의 대역이 다른 방식으로 제한(band-limited)되지 않는다면, 얼라이어싱이 발생할 수 있다.

얼라이어싱 현상을 이해하기 위해 두 개의 사인파를 가지는 일차원 신호를 살펴보자(그림 2.15). 만약 $f=2$의 파장으로 두 신호를 샘플링 한다면, 동일한 샘플로 귀결됨을 알 수 있으며(그림 2.15의 좌측) 이런 현상을 얼라이어싱되었다(aliased)고 표현한다.

얼라이어싱이 발생하면 두 원본 주파수 중 어느 것이 실제로 존재했는지를 알 수 없기 때문에 원래의 신호를 복원할 수 없다. 구체적으로는 어떤 신호를 순간(instantaneous) 샘플로부터 재구성하기 위해 필요한 최소 샘플링 비율은 그 신호의 가장 높은 주파수의 두 배 이상이어야만 한다.

\[f_2 \ge 2f_{\text{max}}\]

이때 최대 주파수를 Nyquist frequency, 샘플링 주파수의 최소값의 역 $r_s=\frac{1}{f_s}$를 Nyquist rate라고 부른다.

그런데, 이미지 센서는 실제로 제한된 영역엥 걸쳐 빛을 평균으로 계산하기에 점 단위 샘플링(point sampling) 이론이 여전히 유효한지에 대해 검증해볼 필요가 있다. 우선, 센서 영역 전체에서의 평균은 일반적으로 고주파 성분을 일부 줄여주는 효과가 있다. 하지만, 그림 2.15의 우측 처럼 충전율이 100%라고 하더라도, Nyquist limit(샘플링 주파수의 절반)를 넘는 주파수 성분은 여전히 얼라이어싱 현상을 유발한다. 다만, 그 신호의 세기는 대역 제한된 신호에 비해 더 작게 나타날 수 있다.

Figure 2.16 2차원 신호의 얼라이어싱 : (a) 원래의 전체 해상도 이미지; (b) 25% 필 팩터 박스 필터로 4배 다운샘플링 된 이미지 ; (c) 100% 필 팩터 박스 필터로 4배 다운샘플링된 이미지 ; (d) 고품질 9-탭 필터로 4배 다운샘플링 된 이미지 ;

얼라이어싱이 왜 문제가 되는지 더 확실히 이해하고자 한다면, 박스 필터와 같은 저품질 필터를 사용해 다운샘플링 한 경우를 확인해보면 된다. 그림 2.16에서는 시간에 따라 주파수가 점점 증가하는 고주파 chirp 이미지와 함께, 이를 25% 충전율 센서, 100% 충전율 센서, 그리고 고품질 9-탭 필터로 샘플링한 결과를 보여준다.

이미 처리 알고리즘이 만들어내는 얼라이어싱의 양을 예측하는 가장 적합한 방법은 점 확산 함수(point spread function, PSF)을 측정하는 것이다. 점 확산 함수는 이상적인 점 광원으로부터의 특정 픽셀이 반응하는 정도를 나타낸다. PSF는 광학 시스템에서 유도된 흐림효과(blur)와 센서의 유한한 통합 면적(finite integration area)이 결합되어 형성된다.

Figure 2.17 PSF : (a)에서 블러 디스크(파란색)의 지름은 픽셀 간격의 절반이다. 반면, (c)에서는 그 지름이 픽센 간격의 두 배이다. 센서 칩의 수평 필 팩터는 80%이며, 갈색으로 표시되어 있다. 이 두 커널을 컨볼루션하면 PSF가 계산되며, 초록색으로 표시되어 있다. PSF의 푸리에 응답은 (b), (d)에 그래프로 나타나있다. Nyquist 주파수를 초과하여 얼라이어싱이 발생하는 영역은 빨간색으로 표시되어 있다.

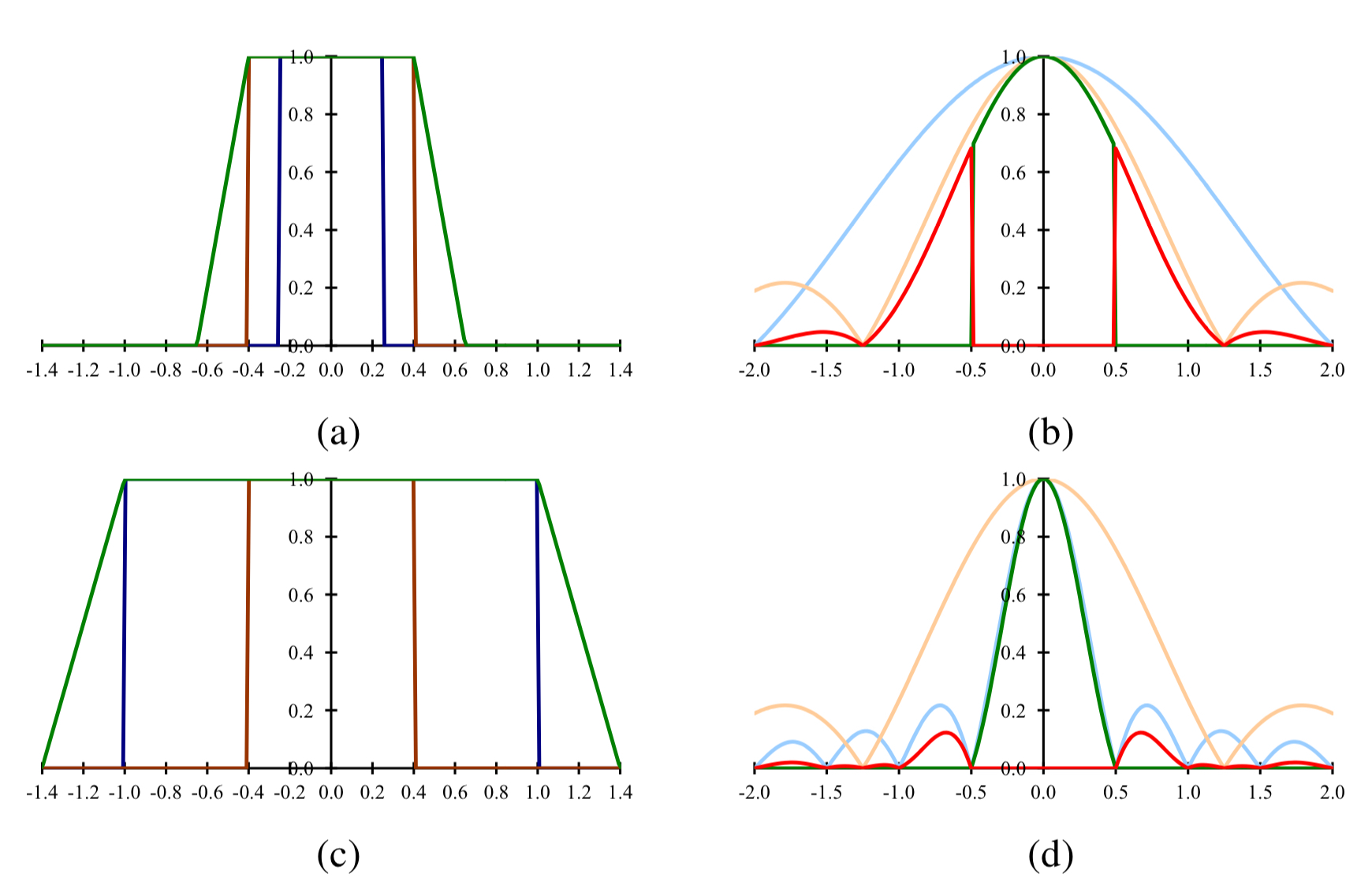
렌즈의 블러 함수와 영상 칩의 필 팩터를 알고 있다면 이들을 결합해 PSF를 구할 수 있다.(3.2장 바로가기 추가) 그림 2.27a는 렌즈의 블러 함수가 반지름 s인 원형이고, 수평 필 팩터가 80%인 센서 칩을 사용하는 경우를 보인다. 이 PSF에 푸리에 변환을 적용하면, 변조 전달 함수(modulation transfer function, MTF)를 얻을 수 있다.(3.4장 바로가기 추가). 이렇게 얻은 MTF를 통해 $f \le f_s$ Nyquist 주파수 바깥의 푸리에 스펙트럼 크기 면적을 계산함으로써 얼라이어싱의 양을 추정할 수 있다. 이 때, 렌즈를 디포커싱해서 블러 함수의 반지름이 $2s$가 되면 얼라이어싱은 확연히 줄어들지만, 동시에 고주파 정보의 손실도 동시에 일어난다.

Digital Camera