심층 신경망(Deep Neural Networks, DNN)은 일관적이고 미분 가능한 계산 구조를 제공하면서, 유용한 내부 표현을 자동으로 학습한다.

Weights and layers

Figure 5.20

Figure 5.21

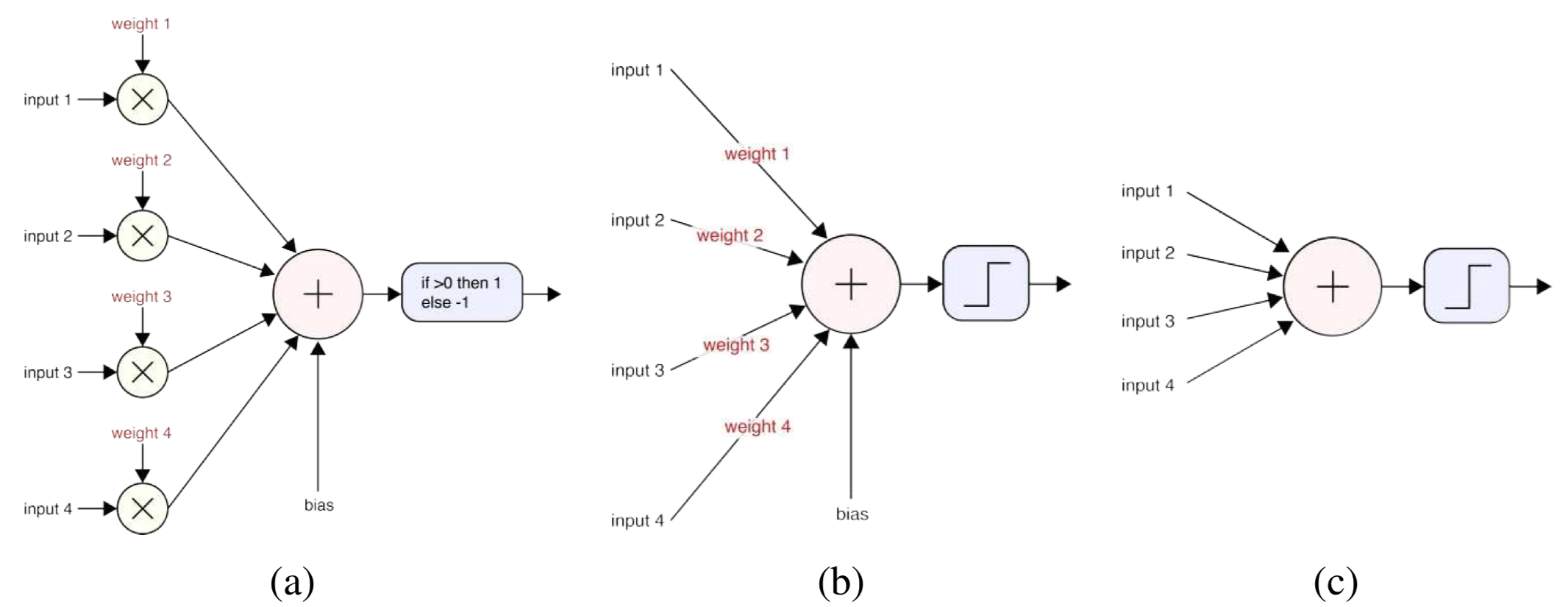
DNN은 수천개의 서로 연결된 뉴런(Neurons)으로 구성된 순방향(feedforward) 계산 그래프이다. 각 뉴런은 로지스틱 회귀와 유사하게 입력값의 가중 합을 계산한 뒤, 비선형 활성화 함수(activation function)로 다시 매핑한다.

\[\begin{align} s_i &= \mathbf{w}_i^\top\mathbf{x}_i+b_i \\ y_i &= h(s_i) \end{align}\]

각각 $\mathbf{x}_i$는 i 번째 뉴런의 입력값, $\mathbf{w}_i, b_i$는 학습 가능한 가중치(weights)와 편향값(bias), $s_i$는 가중선형합(weighted linear sum)의 출력값, $y_i$는 $s_i$를 활성화 함수 $h$에 입력하였을때 출력되는 최종 출력값을 의미한다.

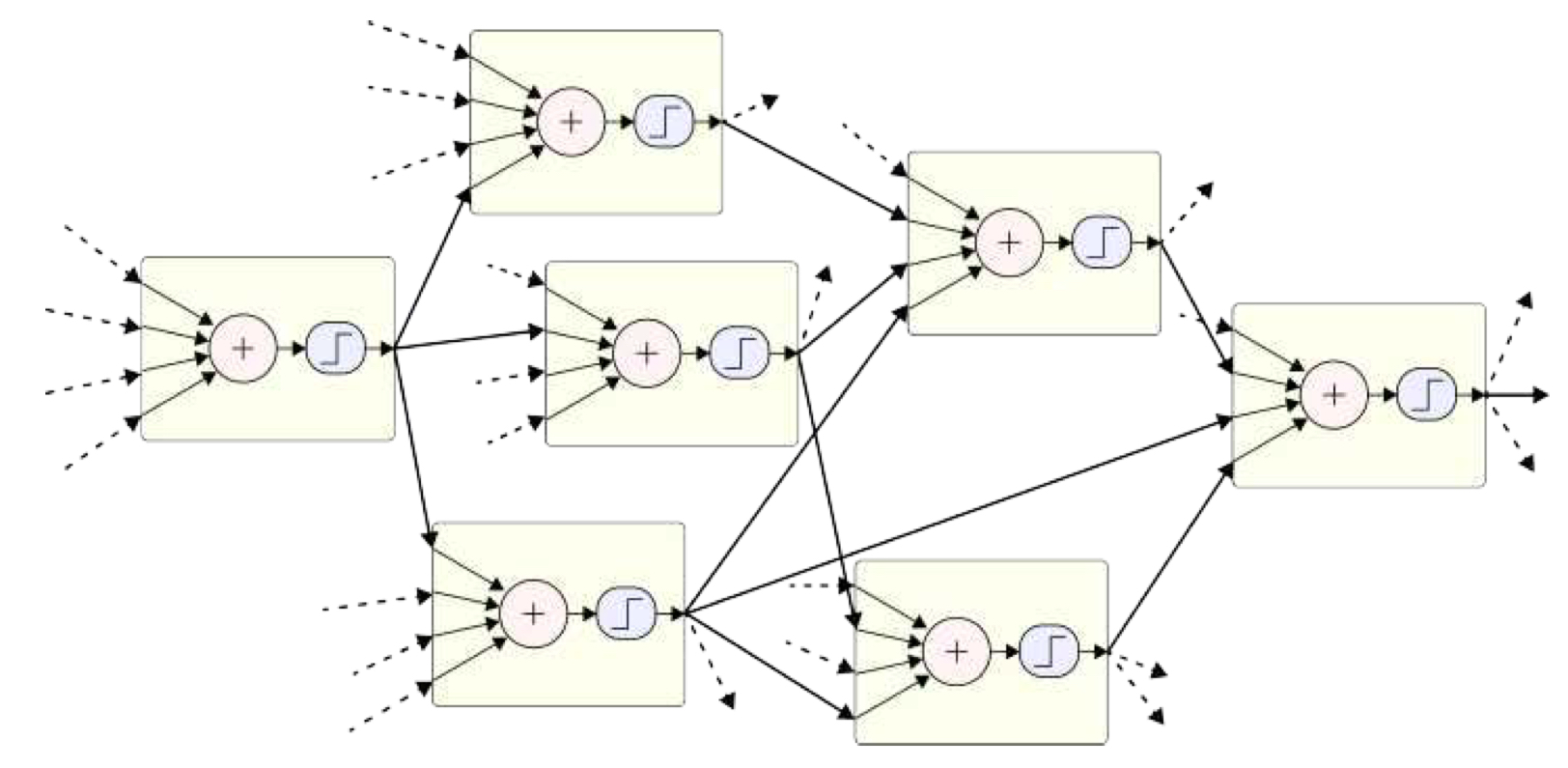
활성값(activations)이라고 불리는 각 단계의 출력값은 그림5.21에 묘사된 것 처럼 다음 단계의 입력값으로 주어진다.

이러한 신경망 뉴런의 최조 형태는 퍼셉트론(perceptron)이라고 불리며 그림 5.20(a)와 같이 표현되었다. 그림(a)에서는 가중치가 학습 과정에서 최적화된다는 점을 고려해 각 연결에서 이루어지는 원소별 곱셈과 함께 명시적으로 표시되어 있다. 그림(b)에서는 가중치가 뉴런 간의 연결을 나타내는 선 위에 표기되어 있으며, 가장 흔히 사용되는 형태인 그림(c)는 가중치와 편향을 완전히 생략하여 그림상에 명시하지 않더라도 내부적으로 존재한다고 간주한다.

Figure 5.22

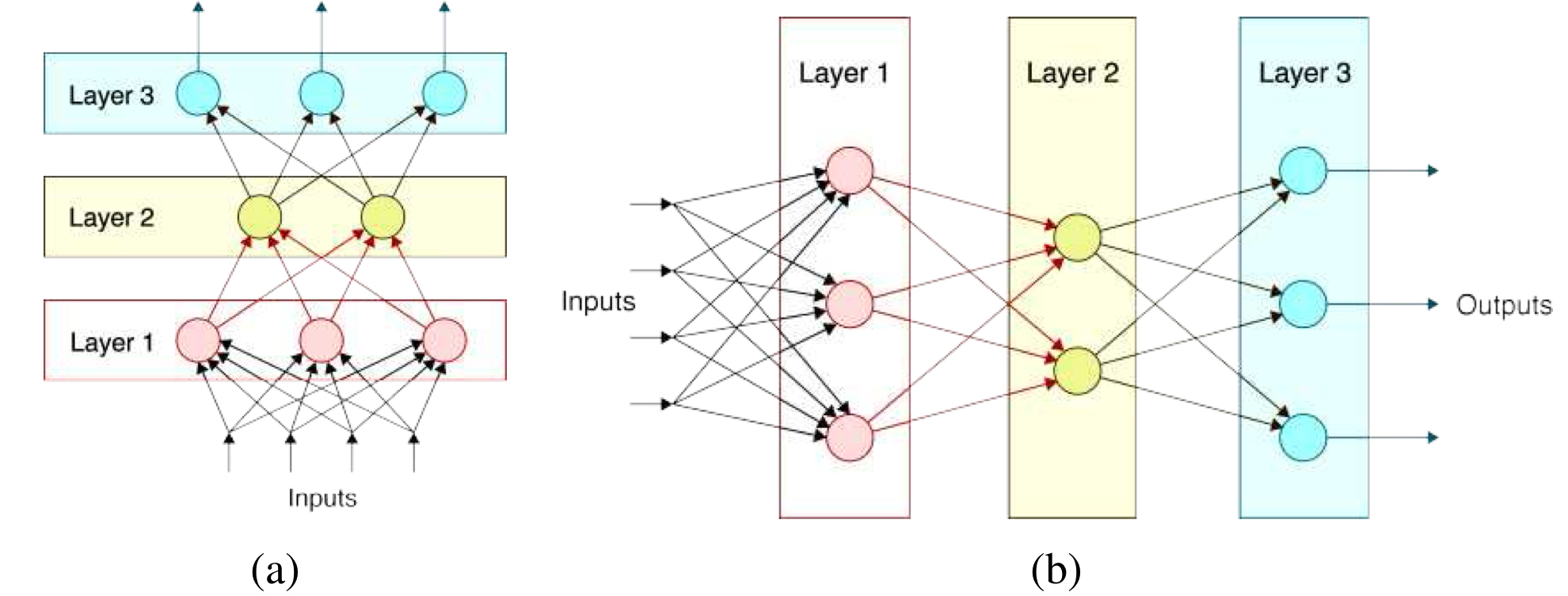
그림5.21과 같은 불규칙한 계산 그래프 형태로 연결되는 대신, 신경망(Neural Networks)는 일반적으로 그림 5.22와 같이 연속적인 레이어(layers) 구조로 조직된다. 이제 각 레이어 안의 모든 뉴런들을 하나의 벡터로 간주할 수 있으며, 이 벡터의 각 원소는 다음과 같은 선형 결합으로 계산된다.

\[\mathbf{s}_l = \mathbf{W}_l\mathbf{x}_l\]

이 때, $\mathbf{x}_l$은 $l$번 째 레이어로 입력되는 입력 벡터, $\mathbf{W}$는 가중치 행렬, $\mathbf{s}_l$은 가중합 벡터를 의미한다.

이후, 각 원소에 비선형 활성화 함수를 원소 단위로 적용하여 다음 레이어의 입력 벡터인 $\mathbf{x}_{l+1}$을 계산한다.

\[\mathbf{x}_{l+1} = \mathbf{y}_l = \mathbf{h}(\mathbf{s}_l)\]

선형 결합시에 완전 연결 가중치 행렬(full weight matrix)을 사용한 레이어는 레이어의 모든 입력이 레이어의 모든 출력으로 연결되어 있기에 _fully-connected(FC)_레이어라고 한다. 또한 FC레이어로만 구성된 네트워크를 multi-layer perceptron(MLP)라고 한다.

Activation functions

Figure 5.23

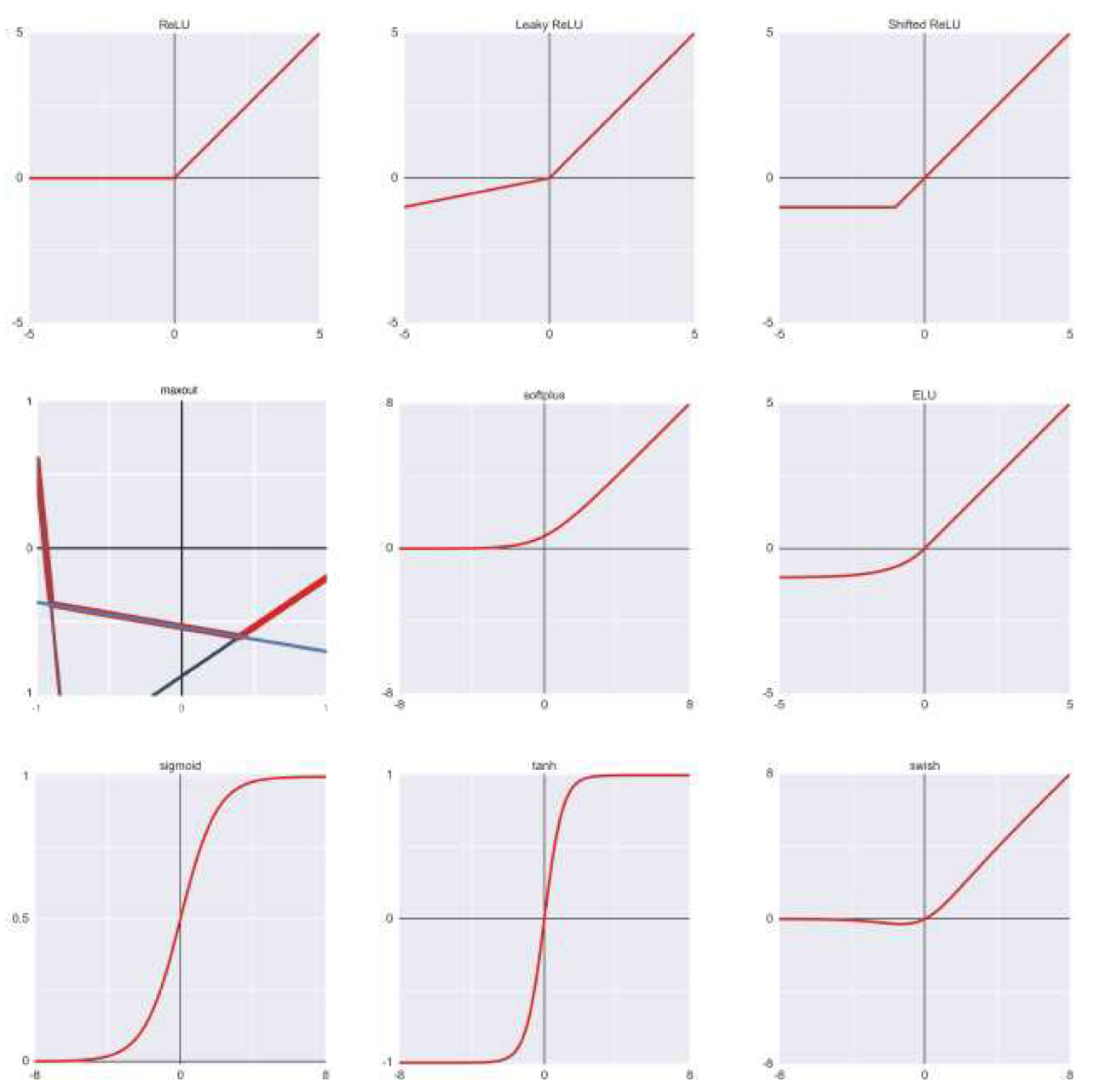
초창기 신경망은 로지스틱 회귀와 유사한 시그모이드 함수를 활성화 함수로 사용했지만, 최근 들어서는 Rectified Linear Unit(ReLU)나 ReLU의 변형을 사용하는 추세이다.

\[h(y)=\max(0,y)\]

다만 ReLU 뉴런은 훈련 중 죽을 수(die)도 있다는 위험성을 가지고 있다. 예를 들어 큰 그래디언트가 흘러들어오면 가중치가 크게 변해, 그 뉴런이 앞으로 어떤 입력에 대해서도 활성화되지 않을 수 있으며, 한 번 죽은 뉴런은 그래디언트가 0이 되어 영구적으로 비활성화된다.

Figure 5.24

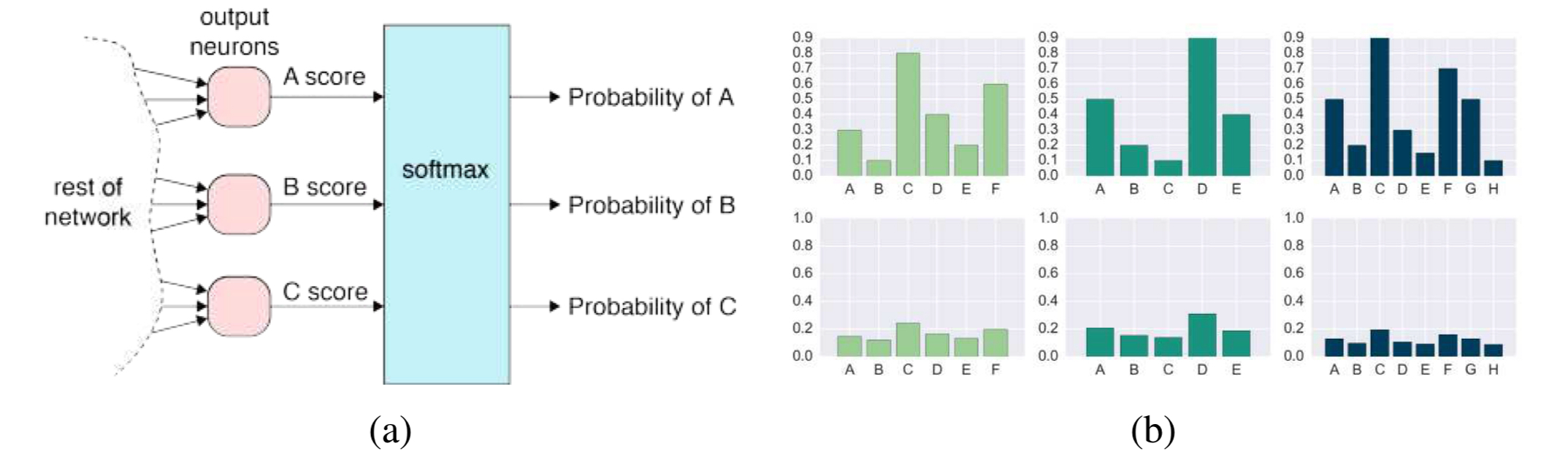
분류 모델의 마지막 레이어에서는 실제 세상의 활성값을 클래스 우도로 변환하기 위해 소프트맥스 함수가 일반적으로 사용된다. 따라서, 끝에서 두 번째 레이어의 뉴런들은 활성화 공간(activation space)에서 각 클래스에 해당하는 로그 우도와 가장 잘 일치하는 방향을 결정한다고 볼 수 있으며, 이와 동시에 다른 클래스들의 로그 우도는 최소화된다.

입력이 최종 출력 클래스와 확률로 순방향으로 흐르기 때문에 순방향 네트워크는 판별(discriminative)모델이다. 즉, 이 모델은 클래스 간 경계를 구분할 수는 있지만, 클래스를 생성하거나 샘플링하는 능력은 없다.

Regularization and normalization

앞으로 서술할 Reularization을 포함한 다른 기법들은 신경망의 오버피팅을 예방해 처음 보는 데이터에 대한 일반화 성능 향상을 도모한다.

Regularization and weight decay

Regularizer

\[E_{\text{W}}=\sum_k \lVert \mathbf{w}_k\rVert^p\]

가중치에 L2 패널티(quadratic) 또는 L1/Lp 패널티 같은 정규화 항을 추가하면, 모델의 수치적 안정성을 높이고 과적합을 방지하는 데 도움이 된다.

$p=2$는 $L_2$ 정규화를 적용시켜 큰 가중치를 작게 만드는 효과를 내며, $p=1$은 LASSO(Least Absolute Shrinkage and Selction Operator)라고 부르는 정규화를 적용시켜 일부 가중치를 완전히 0으로 만드는 효과를 가질 수 있다.

이런 종류의 regularization을 통해 신경망의 가중치를 최적화 시킬 수 있으며, 이를 Weight decay라고 부른다.

Dataset augmentaton

미리 구해놓은 샘플의 입력값이나 출력값을 뒤섞어 훈련 샘플에 추가하는것도 오버 피팅을 방지하는 강력한 방법 중 하나다. 이런 기법을 데이터셋 증강(dataset augmentation)이라고 부르며 특히나 이미지 분류 문제에서 강력한 성능을 보인다.

Figure 5.25

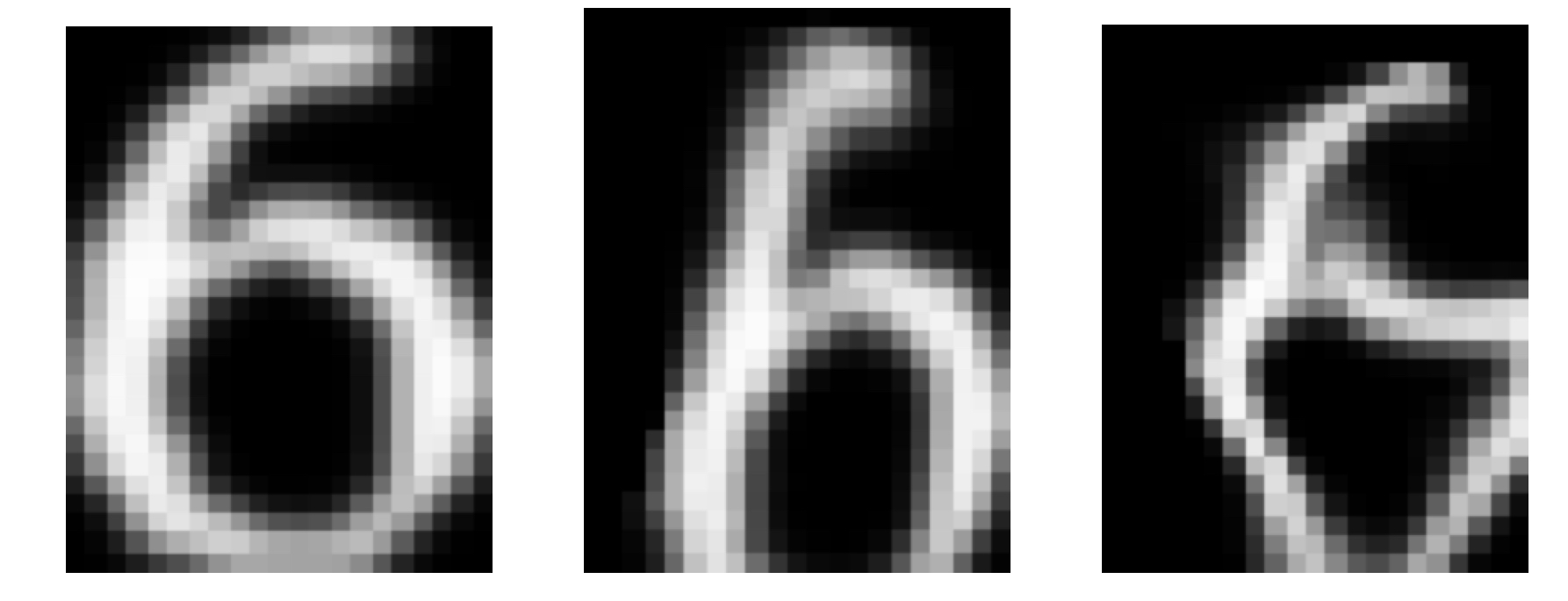
초기 신경망 분류 문제에서는 elastic distortion이라는 기술이 주로 사용되었다. Elastic distortion은 랜덤한 저주파 변위 장을 각 훈련 샘플로부터 생성하여 훈련 과정에 입력값으로 활용한다.

Elastic distortion을 사용해 발생한 왜곡들은 입력값에 단순히 픽셀 노이즈를 삽입하거나 추가하는 방식은 아니다. 장(fields)이라는 용어를 통해 알 수 있듯이 픽셀을 주변으로 움직여 입력값 벡터 공간에 변화를 주는 동시에 입력 샘플의 ‘맥락’을 유지한다.

Dropout

Figure 5.26

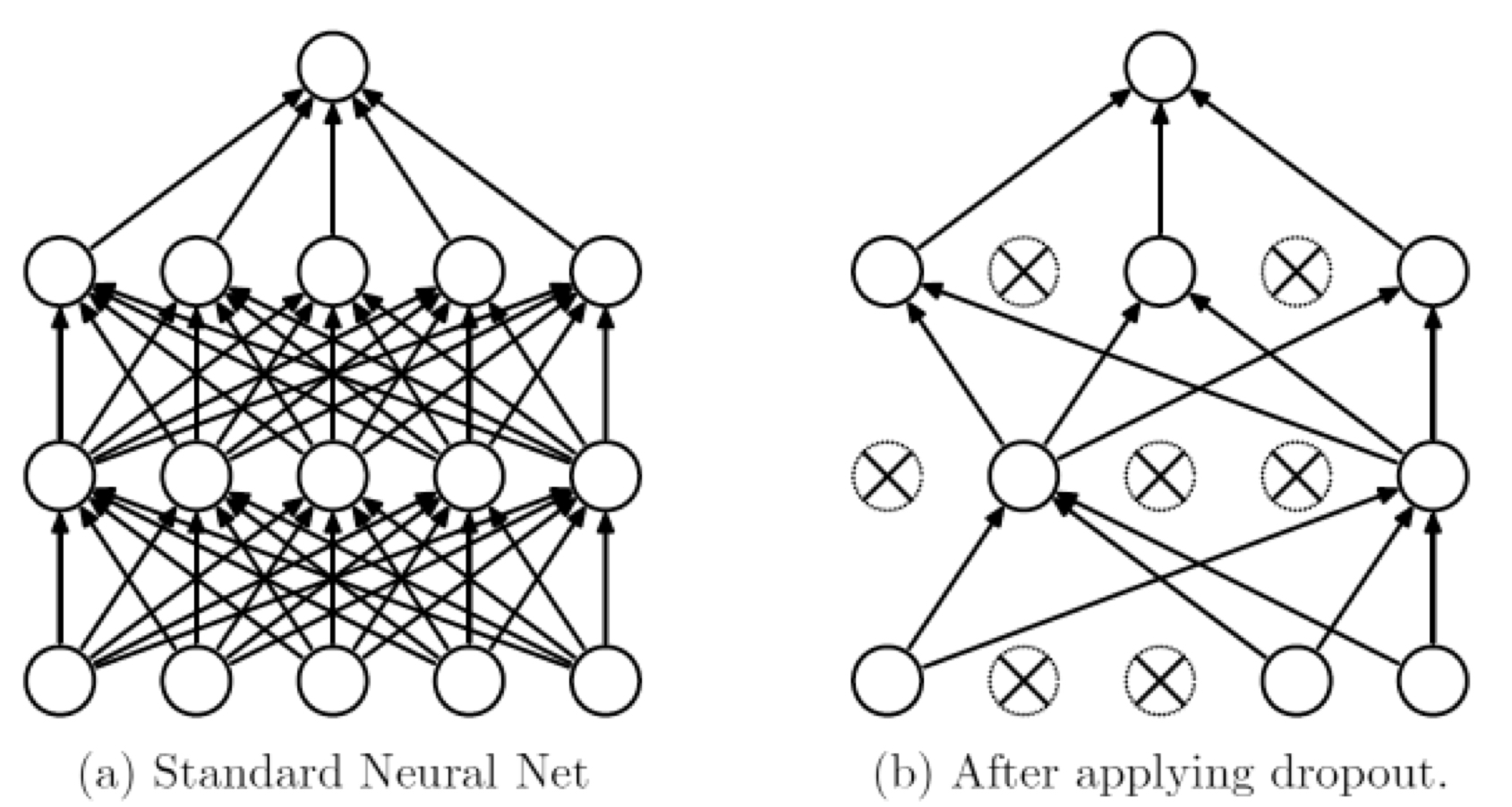
Dropout은 미니배치의 훈련 과정에 각 레이어에 속한 특정 비율 $p$ 만큼의 뉴런을 0으로 만들어버린다. 랜덤한 비율의 뉴런을 0으로 만들어 훈련 과정에 삽입해 노이즈를 만들고, 신경망의 특정 뉴런이 특정한 샘플에 과도하게 적응하는것을 예방한다.

뉴런 중 $p$ 만큼을 제거하면, 그 뉴런이 기여하는 합의 기대값이 $(1-p)$ 만큼 줄어들기 때문에, 각 층에서의 가중합 $s_i$는 학습시에 $(1-p)^{-1}$로 곱해진다. 테스트 과정에서는 Dropout 없이 전체 뉴런을 다 사용하므로 별도의 보정을 하지 않는다.

Batch normalization

반복적 최적화(iterative optimization)에서는 종종 gradient의 각 요소들이 스케일이 너무 달라서 학습이 잘 안 되는 문제가 발생하는데, 이러한 현상을 “컨디셔닝이 나쁘다(poor conditioning)”고 표현한다.

나쁜 컨디셔닝 문제를 해결하기 위해서 단계를 밟기 전에 각 원소의 gradient를 scale 하는 것 과 같이 preconditioning 기법을 사용하는 것도 유용하다.

Poor conditioning이란?

수치 최적화에서, 변수 방향마다 스케일이 너무 다르거나 일부 방향에서는 gradient가 거의 0에 가까워 수렴이 느려지는 문제를 말한다. 이 문제로 인해 학습 속도가 느려지거나, gradient descent가 지그재그로 수렴하거나 발산할 수 있다.

깊은 신경망에서 나쁜 컨디셔닝 문제가 나타나는지 확인하는 방법은 층 간 가중치나 출력 크기 불균형이 관찰되는 경우이다. 예를 들어, 한 층을 100 배 크게 만들고 다음 층을 100배 줄이면 ReLU 활성 함수는 정의역 전체에서 선형이기에 두 번째 층의 출력은 여전히 동일하지만, 내부 값들이 왜곡된다. 이로 인해 역전파 시 gradient가 왜곡되며, 너무 크거나 작은 값이 발생해 오버 슈팅(Overshooting)이 발생할 수 있다. 따라서 매우 작은 학습률을 요구하게 된다.

배치 정규화(Batch normalization)의 아이디어는 특정 뉴런의 활성화를 다시 스케일링 해서 뉴런들을 표준 정규 분포(분산이 1이고 평균이 0인, zero-mean unit-variance)로 만든다. Batch Normalizaton에서는 각 미니 배치 $\mathcal{B}$ 내의 데이터를 기준으로 각 뉴런 $i$의 평균과 분산을 계산하여 정규화를 수행한다.

\[\begin{align} \mu_i &= \frac{1}{\lvert \mathcal{B} \rvert}\sum_{n\in\mathcal{B}}s_i^{(n)} \\ \sigma_i^2 &= \frac{1}{\lvert \mathcal{B} \rvert}\sum_{n\in\mathcal{B}}(s_i^{(n)} - \mu_i)^2 \\ \hat{s}_i^{(n)} &= \frac{s_i^{(n)}-\mu_i}{\sqrt{\sigma_i^2+\epsilon}} \end{align}\]

위 수식에서 $s_i^n$은 훈련 샘플 $n$의 뉴런 $i$의 가중합(weighted sum)을, $\hat{s}^{(n)}_i$는 그에 대응되는 배치 정규화된 합을, $\epsilon$은 0으로 나눠지는 것을 방지하기 위한 상수이다.

Batch normalization이 끝난 후 활성값 $\hat{s}^{(n)}_i$은 평균이 0이 되고 분산이 1로 변환되었다. 또한 Batch normalization은 과정을 거친 후에 항상 평균 0, 분산 1로 고정되기에 비선형성의 작동 범위를 제한할 수 있다. 이를 해결하기 위해 각 뉴런 $i$에 대해 학습 가능한 스케일 $\gamma_i$와 시프트 $\beta_i$를 적용함으로써 모델이 표현력을 유지할 수 있도록 보완한다.

\[y_i=\gamma_i\hat{s}_i + \beta_i\]

스케일과 시프트는 일반적인 가중치처럼 작동하며 훈련 과정 중 경사 하강법을 통해 수정되어 전체 훈련의 손실을 줄이는 효과를 가진다.

Batcn Normalization은 평균 $\mu_i$과 분산 $\sigma_i^2$ 값들이 미니 배치 내 전체 활성값에 의존하므로 이 값들이 고정 상수가 아니라 계산 그래프 내의 변수처럼 취급되어야 한다. 따라서, backpropagation 시 손실 함수가 이들에 대해 어떻게 변화하는지도 미분해줘야 하며, 기존 backpropagation 처럼 체인 룰을 통해 gradient를 전파해야한다.

Batch Normalization을 컨볼루션 신경망에 적용할 때는, 공유되는 커널로부터 얻은 여러 위치의 픽셀들의 값을 모아 평균과 분산 등의 통계치를 산출하고, 이를 바탕으로 각각의 컨볼루션 커널마다 하나의 스케일과 시프트 파라미터를 추가하는 방식으로 구현된다.

훈련 과정 중에는 배치 단위로 평균/분산을 계산하지만, 테스트나 추론 과정 중에 입력되는 새로운 데이터에 대해서는 그렇게 할 수 없다. 따라서 다음 두 가지 방법이 사용된다.

전체 훈련 세트에 대해 평균과 분산을 다시 계산
훈련 중 저장해둔 평균과 분산(running mean/variance)를 사용

Figure 5.27

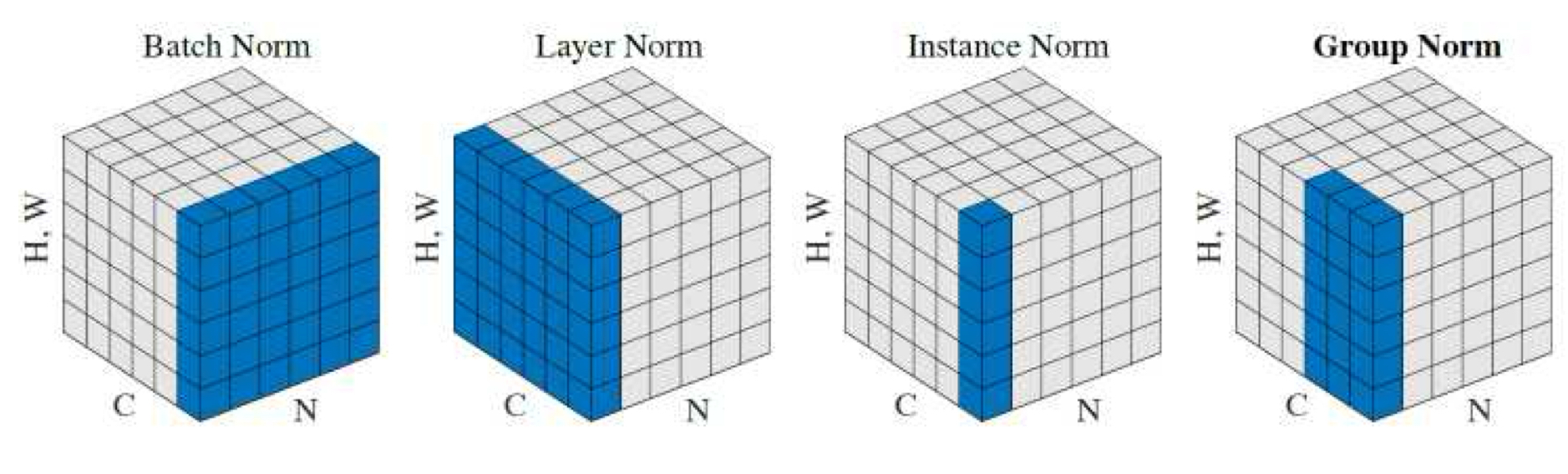
수식이 선형 형태를 띄기 때문에 파라미터들을 기존의 가중치와 바이어스에 흡수시켜 추론 과정에서 BN레이어를 제거하여 효율적으로 계선하는 방법도 있다. Batch Normalization 이후에는 다양한 변형이 등장했고, 일부는 배치가 아닌 다른 단위로 정규화 통계를 계산하는 방식을 사용한다.

정규화 방식	정규화 대상	계산 범위
Batch Normalization	동일 채널, 미니배치 내 모든 위치	(N, H, W)
Layer Normalization	한 샘플의 전체 뉴런	(C, H, W) or (C,)
Instance Normalization	한 샘플, 한 채널 내 모든 위치	(H, W)
Group Normalization	여러 채널을 그룹으로 묶어 정규화	(G, H, W)
Weight Normalization	가중치 벡터의 방향과 크기를 분리하여 정규화	각 뉴런의 가중치 벡터
Spectral Normalization	가중치 행렬의 스펙트럼 노름 제어	가중치 행렬 $W$

Loss functions

신경망의 가중치를 최적화하기 위해서는 학습 데이터를 기반으로 손실 함수를 정의한 뒤 이 손실을 최소화하도록 가중치를 조정해야한다.

분류 문제에서 대부분의 신경망은 마지막 층을 소프트맥스 함수를 적용한다. 이 경우, 출력값이 총합이 1인 클래스 확률로 정의되기에 훈련 과정 중 손실을 최소화 하기 위해 크로스-엔트로피 로스를 적용한다. 순전파 네트워크의 경우 뉴런을 $i,j$로 작성했지만, 손실 함수를 설명하는 과정에서 특정한 뉴런(훈련 샘플)은 $n$으로 표기하겠다.

$n$으로 뉴런을 표기하면 멀티 클래스 크로스 엔트로피 손실을 다음처럼 작성할 수 있다.

\[E(\mathbf{w}) = \sum_nE_n(\mathbf{w})=-\sum_n\log p_{nt_n}\]

이 때 $\mathbf{w}$는 가중치, 편향값을 포함한 벡터의 모든 모델 파라미터이고, $p_{nk}$는 올바른 클래스를 표기하는 상수이다.

Supervised Learning에서 소개된 $p_nk$의 정의에서 $l_{ik}$를 신경망에서 사용하는 표기인 $s_{nk}$로 대체하여 대입하면 다음 식을 얻을 수 있다.

\[E_n(\mathbf{w}) = \log Z_n - s_{nt_n}\]

이 때 $Z_n = \sum_j \exp s_{nj}$다.

깊이 맵과 같이 한 개 이상의 연속적인 변수를 생성하는 회귀 문제에서는 $L_2$ 손실을 사용하는게 일반적이다.

\[E(\mathbf{w}) = \sum_n E_n(\mathbf{w}) = - \sum_n \lVert \mathbf{y}_n - \mathbf{t}_n \rVert^2\]

이 때 $\mathbf{y}_n$은 샘플 $n$의 신경망 출력값이고, $\mathbf{t}_n$은 상응하는 타겟 값이다. 이는 연속적인 변수들 사이의 오차를 측정하기에 자연스러운 척도라고 볼 수 있다.

위 손실 함수들은, 사실상 정답에 대한 확률 가중치를 최대화 하도록 신경망을 유도할 뿐 신경망의 출력이 적절한 신뢰도 보정(confidence calibrated)을 하도록 만들지는 않는다. 신뢰도 보정 문제를 해결하기 위해 _temperature_에 로그 우도를 곱하는 간단한 방법들도 실제 확률과 분류기의 확률의 정확성 향상에 도움을 주며, 대표적으로 GrokNet을 들 수 있다.

새로운 이미지를 생성하는 신경망이나 이미지 스타일 전이 작업을 수행하는 경우 perceptual loss를 사용하는 것이 더 적절할 수 있다. Perceptual loss는 목표 이미지와 출력 이미지 간의 비교 기준으로 은닉층의 반응을 사용한다.

합성된 이미지의 완성도를 평가하기 위해 별도의 판별 신경망(discriminator network)를 훈련시키는 방법도 있고, 이미지 합성에 손실 함수를 적용하는 방법도 있다.

일반적으로 손실 함수는 지도 학습에 사용되어왔지만, 비지도 학습에서도 사용이 가능하다. 대표적인 사례로 대조 손실 함수(constrastive loss function)은 유사한 샘플들은 서로 가깝게, 유사하지 않은 샘플들은 서로 떨어지도록 임베딩 공간에서 구성하는 방식이다.

입력 샘플 집합$\lbrace x_i \rbrace$과 샘플 쌍의 유사도를 나타내는 쌍별 표시 변수(pairwise indication)$t_{ij}$를 활용하여 각 입력 $x_i$에 대해 임베딩 $v_i$를 계산하는 것이 대조 손실 함수의 목표이다. 이처럼 샘플 간 의미 있는 거리를 생성하도록 매핑이나 임베딩을 학습하는 것을 메트릭 학습(metric learning)이라 하며, 메트릭 학습을 포함해 의미 있는 거리 구조를 유도하는 손실 함수들을 ranking losses로 통틀어 부른다.

대조 손실(constrastive loss)은 다음과 같이 정의된다.

\[E_{\text{CL}} = \sum_{(i,j)\in \mathcal{P}} \lbrace t_{ij} \log L_S(d_{ij}) + (1-t_{ij}) \log L_D (d_{ij}) \rbrace\]

이 때 $\mathcal{P}$는 라벨링 된 입력값 쌍의 집합이며, $L_S, L_D$는 각각 유사(similar) 함수와 비유사(dissimilar) 손실 함수이다. 또한, $d_{ij} = \lVert \mathbf{v}_i - \mathbf{v}_j \rVert$는 임베딩 쌍 간의 거리이다. 위 수식은 임베딩 $\mathbf{v}_i, \mathbf{v}_j$ 사이의 거리를 제곱 해서 계산한다는 점을 제외하고는 크로스 엔트로피 손실과 유사한 형태를 가진다.

대조 손실을 사용해 학습하기 위해서는 입력값 쌍을 신경망에 통과시키고, 손실값을 계산한 후 그 손실에 대한 기울기를 신경망의 두 경로에 대해 역전파 하면 된다. 이 방식은 가중치를 공유하는 두 개의 동일한 네트워크 복제본으로 구성된 Siamese network를 구성하는 것으로도 이해할 수 있다.

더불어, 삼중 손실(triplet loss)을 구현하는 것도 가능하다. 삼중 손실 함수는 유사한 샘플 쌍과 유사하지 않은 세 번째 샘플을 입력으로 받아 유사하지 않은 샘플 간의 거리가 유사한 샘플 간의 거리보다 일정 마진만큼 더 크도록 학습을 유도한다.

대조 손실과 삼중 손실 모드 시각적 유사성 탐색 학습에 사용될 수 있다. 또한, 신경망의 비지도 선행 학습에도 사용되는 추세이다. 비지도 선행 학습의 경우에는 소프트맥스와 멀티 클래스 크로스 엔트로피로부터 유도되는 약간 다른 대조 손실을 사용한다. 이 때, 손실을 계산하기 전에 임베딩을 모드 단위노름으로 정규화시킨다 ($\lVert \hat{\mathbf{v}}_i\rVert^2 = 1$). 그러고 난 뒤, 다음 손실 함수를 모든 유사한 임베딩 쌍에 대해 합산한다.

\[l_{ij} = - \log\frac{\exp(\hat{\mathbf{v}}_i\cdot\hat{\mathbf{v}}_j / \tau)}{\sum_k \exp(\hat{\mathbf{v}}_i\cdot\hat{\mathbf{v}}_k/\tau)}\]

여기서 분모는 매칭되지 않는 샘플들에 대해서도 합산한다.

위 수식의 $\tau$는 temperature를 의미하며 클러스터가 얼마나 가까이에 붙어있을지를 통제한다.

가중치 초기화

신경망의 가중치를 최적화 하기 전에, 우선, 가중치를 초기화 해야 한다. 초기 신경망은 대칭성을 줄이기 위해 작은 랜덤 값의 가중치를 사용했는데, 이는 모든 뉴런이 동일하게 동작하지 않도록 하여 그래디언트가 0이 되는 상황을 방지하려는 목적이었다.

다만 신경망의 층이 깊어질수록 활성값이 점점 작아지는 현상이 관찰되었고, 이를 해결하기 위해서는 연속된 층들의 활성값 분산이 일정하게 유지되도록 해야한다. 이를 위해 각 층의 입력 연결 수(fan-in)를 고려해야 한다. 이 입력 연결 수는 활성값이 가중치와 곱해지는 횟수로 해석할 수 있다.

대부분의 현대 딥러닝 모델은 ReLU를 사용하므로 각 층 $l$의 가중치를 평균은 0, 분산을 $V_i$로 초기화하고 바이어스를 0으로 설정하면 선형 합 $s_i$의 분산은 다음과 같다.

\[\text{Var}\lbrack s_l \rbrack = n_lV_l\mathbb{E}\lbrack x_i^2 \rbrack\]

이 때 $n_l$은 입력 가중치/활성값의 계수, $\mathbb{E}\lbrack x_l^2 \rbrack$은 입력값의 제곱의 기댓값이다.

이때 $s_l$은 0의 평균을 가지므로 ReLU를 통과하면 음수는 모두 0으로 클램핑 되며 다음이 성립한다.

\[\mathbb{E}\lbrack y_l^w \rbrack = \frac{1}{2} \text{Var}\lbrack s_i \rbrack = \frac{1}{2} n_l V_l \mathbb{E}\lbrack x_l^2 \rbrack\]

이 결과로부터 깊은 층에서도 평균 활성값이 변화하는 현상을 피하려면 각 층의 활성값의 크기를 유지하도록 **가중치 분산$V_l$을 다음과 같이 설정해야 한다.

\[V_l = \frac{2}{n_l}\]

이러한 초기화 방식을 He 초기화(He initialization)라고 부른다.