Batch Normalization : Accelerating Deep Network Training by reducing Internal Covariate Shift

2015, Ioffe, Szegedy

Skim & Map

연구 질문 각 네트워크 입력값의 분산이 학습 과정 중에 변화(학습 중 내부 활성값 분포의 변화, Internal Covariate Shift)하면서 딥 뉴럴 네트워크의 학습을 복잡하게 만들고 있음. 이는 낮은 학습율과 파라미터 초깃값에 세심한 주의를 기울여야 한다는 점에서 비선형성이 많은 모델 구조의 학습을 어렵게 만듬.
주요 기여 Batch-Norm을 통해 이전보다 더 높은 정도의 학습율을 사용할 수 있게 되었으며, 초깃값에 덜 민감하면서도 기존 최고 성능 모델을 능가하는 효율과 성능을 보임. 또한, 자체적으로 정규화 하기에 이전까지 주로 사용되어왔던 Dropout의 사용 빈도나 필요성이 줄어드는 경향이 있음. 또한, 기존 whitening 방식은 계산량이 많아 비효율적이었으나 BN은 미니배치 기반의 근사 정규화를 통해 이를 효율적으로 대체.
한계 RNN에서는 시간축의 정규화가 어렵고, 배치 간 통계치 공유가 모델 특성과 충돌할 수 있어 Batch-Norm의 직접 적용이 어려움. 이에 대한 연구가 이후 과제로 제안됨.

Summary

Problem

레이어 입력값의 분산이 변화하면 레이어들은 새로운 분산에 계속해서 적응해야 하는 문제점이 발생한다. 따라서 학습 시스템의 입력값 분산이 변화하면 Internal Covariate Shift 문제를 겪게 된다. 이전까지는 Domain adaptation 을 통해 해결해 왔지만, Internal Covariate Shift 의 개념은 전체 데이터셋 수준 뿐 만 아니라 서브네트워크, 하나의 레이어 등 내부 레이어 간 분포에도 적용될 수 있다. 이는 훈련 시 높은 학습률을 사용할 수 없으며, 수렴 속도도 감소시킨다.

Key Idea

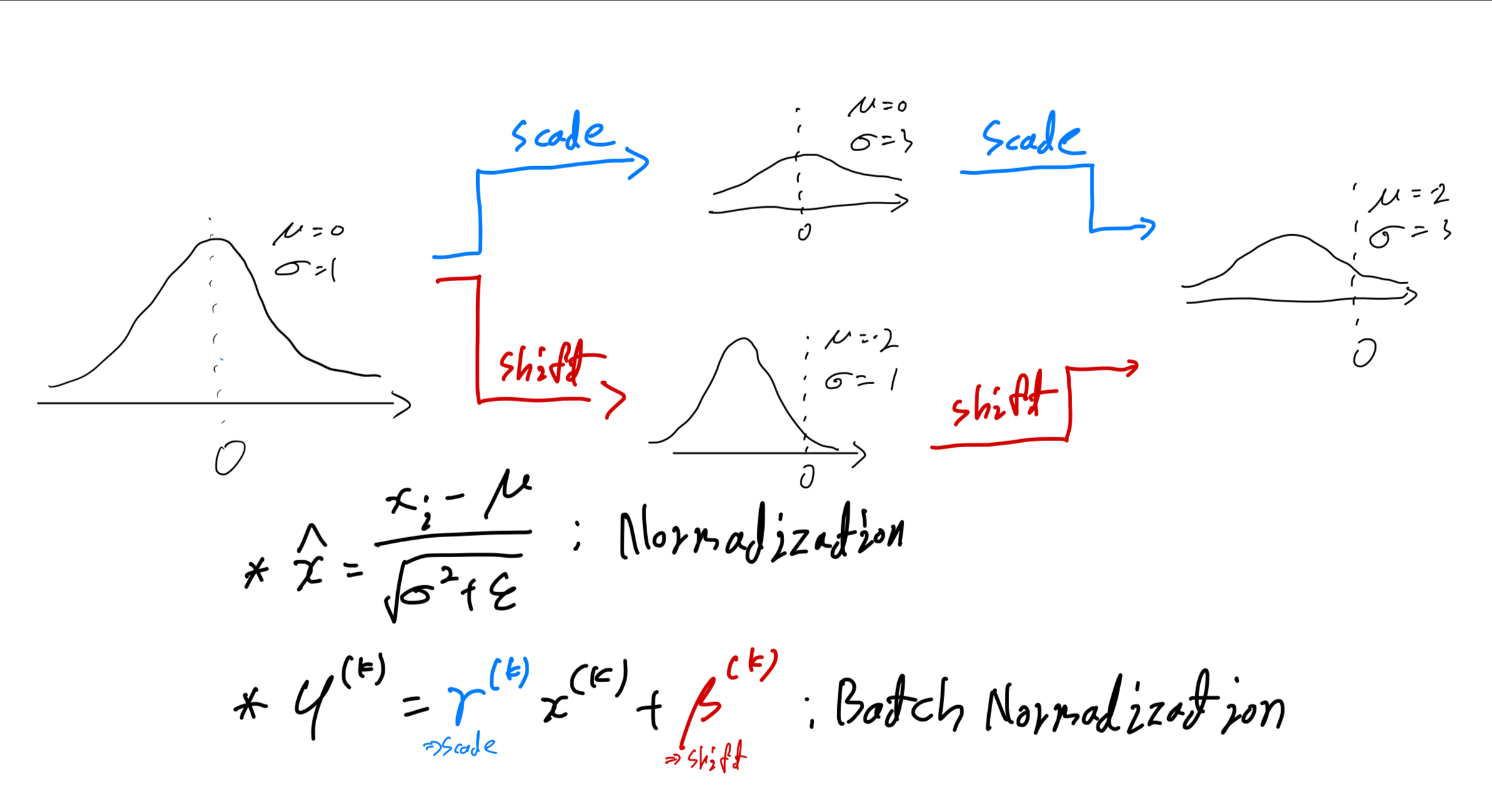
미니배치마다 각 활성 $x^{(k)}$를 독립적으로 정규화해 $\hat{x}^{(k)}$를 얻는다.
표현력 손실을 막기 위해 학습 가능한 적당한 스케일과 시프트 $\gamma^{(k)},\beta^{(k)}$를 적용한다. $y^{(k)} = \gamma^{(k)}\hat{x}^{(k)} + \beta^{(k)}$
추론때에는 학습 동안 누적된 미니배치 통계(평균과 분산)로 변환을 수행한다.

Method

Training with Batch Normalization

적당한 모델 파라미터는 학습을 통해 찾는다. 각 BN 층마다 $k$개의 $\gamma,\beta$를 로스가 줄어드는 방향으로 학습시킨다. 그렇지만 모든 학습 데이터 전체로 계산하기는 불가능에 가까우므로 데이터 전체(Batch)가 아닌 미니 배치마다 BN을 수행한다.

학습 시 미니배치 단위로 평균 및 분산을 계산하고 정규화한 후, $\gamma, \beta$로 아핀 변환을 적용한다.

위 BN 알고리즘에 따르면 Backpropagation을 통해 파라미터 $\gamma,\beta$를 학습할 수 있어야 한다.

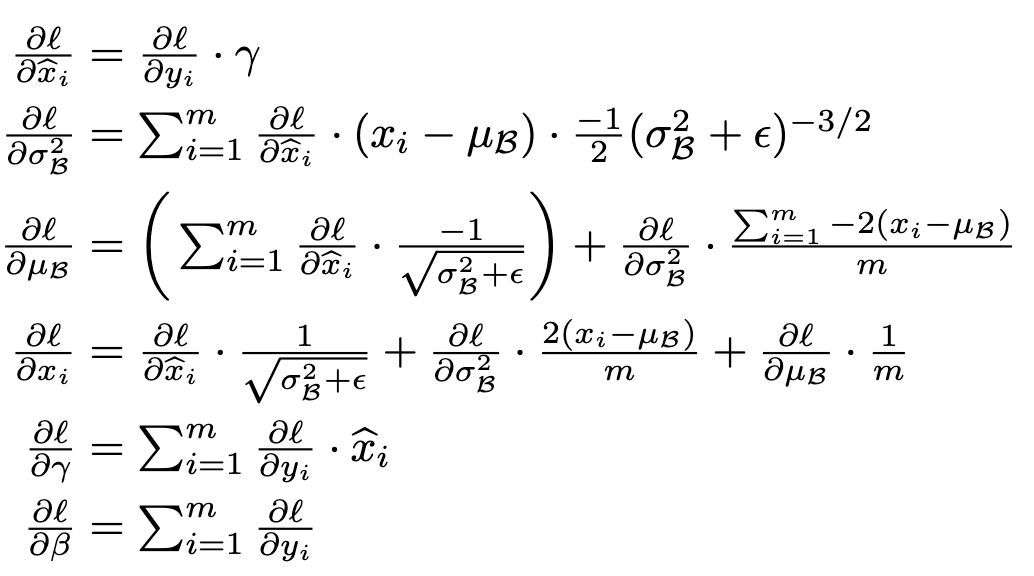
$\gamma, \beta$ 모두 손실에 대해 미분가능하므로 Backpropagation을 통해 학습할 수 있다.

Inference with Batch Normalization

미니배치에 의존하는 활성값의 정규화는 효율적인 학습을 도모하지만 미니배치 기반 통계는 불안정하며 실시간 데이터 적용이 어려운 만큼 추론때에 사용할 정도로 합리적이지 않다. 따라서 네트워크가 학습을 마치면 미니배치 통계가 아닌 전체 통계를 사용해 정규화를 적용한다.

\[\hat{x} = \frac{x-E\lbrack x \rbrack}{\sqrt{\text{Var}\lbrack x\rbrack+\epsilon}}\]

정리하자면 학습 단계의 정규화에서 사용하는 평균과 분산은 학습 데이터 미니 배치의 평균과 분산을 사용하고, 추론 단계에서의 정규화는 학습 단계에서 쌓이는 미니 배치들의 평균과 분산의 이동 평균값을 사용한다.

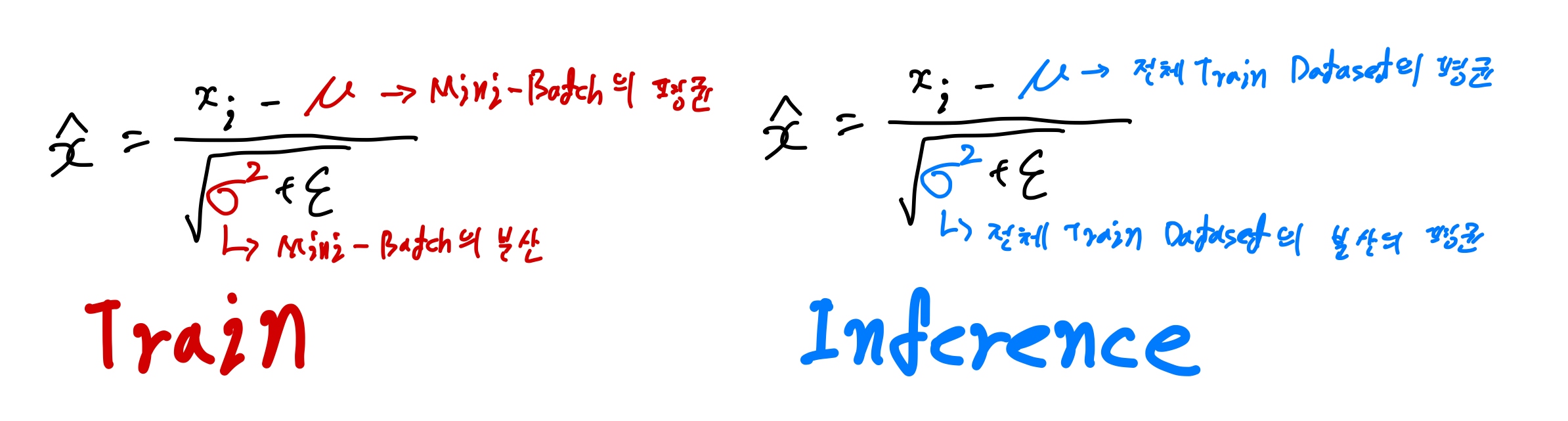
위 과정을 논문에서는 다음 알고리즘으로 표현한다.

Results

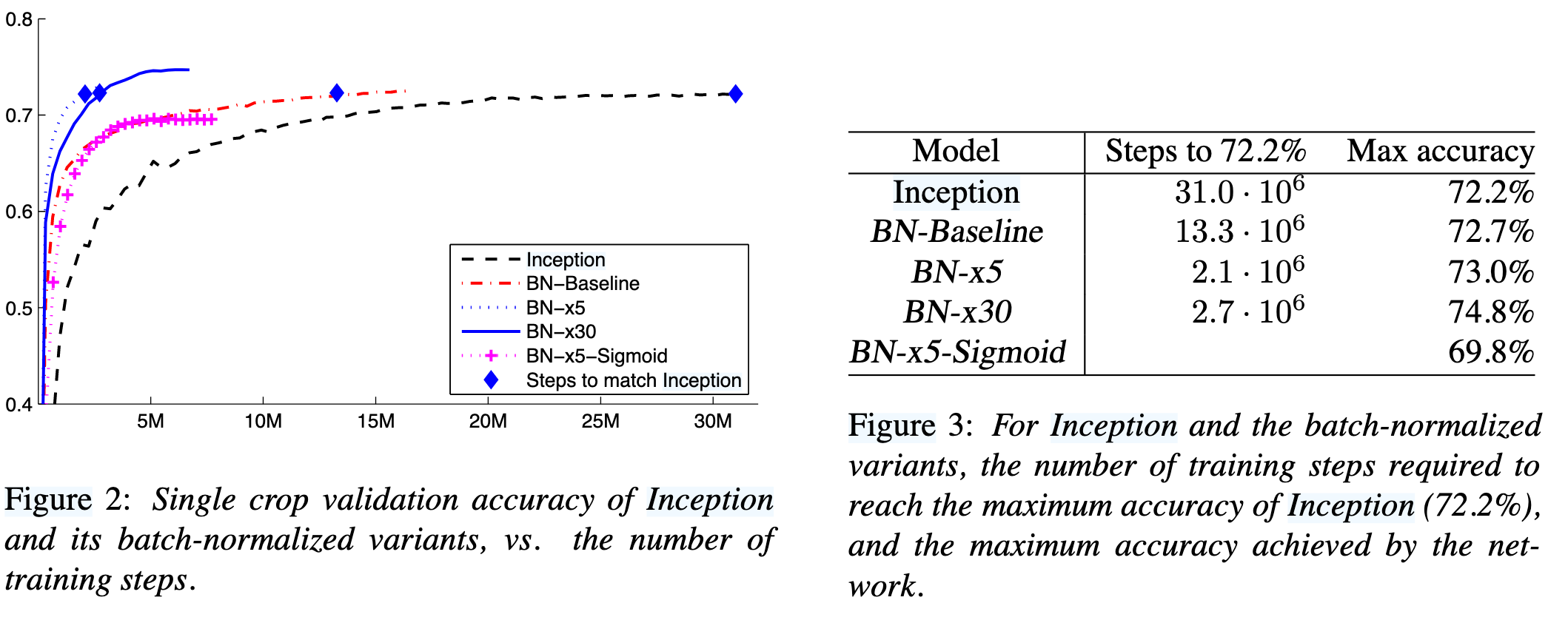
위 그림은 논문에 수록된 여러 모델의 학습 진행 상황에 따른 ImageNet 정확도를 나타낸 그래프이다.

첫 째로, ‘Inception’과 ‘BN-Baseline’ 모델을 비교하면, 인셉션 모델에 BN을 단순히 적용만 했음에도 불구하고 학습 속도가 절반 이하로 단축되는 결과를 볼 수 있었으며 이는 Covariate Shift의 완화로 인한 효과로 볼 수 있다.

두 번째로 ‘BN-Baseline’, ‘BN-x5’, ‘BN-x30’을 비교하면, Learning Rate를 각각 5배, 30배 적용했을 때 학습 속도도 빠르고 성능도 월등히 좋아졌음을 알 수 있다. ‘BN-x5-Sigmoid’ 모델의 곡선을 보면 그 이유를 알 수 있는데, 기존 시그모이드 모델에서는 높은 LR을 적용시켰을 때 발생하는 기울기 소실(Gradient Vanishing) 문제를 BN이 효과적으로 완화함을 보여준다. 이는 BN이 학습률 향상 및 깊은 신경망의 Gradient 전달 경로 개선에 핵심적으로 역할함을 알 수 있다.

Strength

Learning Rate 증가 가능
초기화 민감도 감소
Additional한 regularization 없이도 과적합을 완화
Backpropagation 호환 가능하며 구현도 간단함

Weakness / To-Try

BN은 미니 배치의 크기에 크게 의존성을 가진다. 미니 배치의 평균과 분산으로 정규화를 하기에 미니 배치의 사이즈가 작을수록 평균과 분산은 학습 데이터의 전체 평균, 분산과는 다른 값이 계산될 가능성이 크고, 따라서 각 배치의 정규화때마다 데이터들의 방향이 모델 수렴 방향을 불규칙하게 만들어 학습 성능 저하를 초래할 수 있다. 상술한 문제점은 이후 LayerNorm (Ba et al., 2016), GroupNorm 등의 후속 연구로 이어진다.

REVIEW - Batch Normalization