Batch Normalization : Accelerating Deep Network Training by reducing Internal Covariate Shift

2015, Ioffe, Szegedy

Internal Covariate Shift

E[x]를 역전파와 분리한 L2 Normalization과 Batch Normalization의 Loss를 비교해보자

Modul import

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

torch.manual_seed(0)

Dataset

N = 500
x = torch.linspace(-1,1,N).unsqueeze(1)
y = 2 * x + 0.1 * torch.randn_like(x)

L2Norm model

class L2(nn.Module):
    def __init__(self,eps=1e-6):
        super().__init__() # 클래스 초기화
        self.fc1 = nn.Linear(1,10) # 입력 차원 1 -> 출력 차원 10의 Fully Connected Layer, Weight(10,1), bias(10,)구조로 학습
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(10,1) # 은닉층 출력 10차원 -> 최종 출력 1차원의 Fully Connected Layer

        self.eps = eps

    # mean의 dim=0인 이유는 배치 전체에서 피처별 평균을, std의 dim=1인 이유는 샘플별 벡터 크기 기준으로 정규화 하기 위해서
    def forward(self, x):
        x = self.fc1(x)

        m = x.mean(dim=0, keepdim=True).detach() # detach()를 통해 E[x]의 그래디언트 차단
        std = torch.norm(x-m, dim=1, keepdim=True).detach() + self.eps # 마찬가지로 L2 Norm에 대한 그래디언트 차단

        x = (x-m)/std # L2 Norm
        x = self.relu(x)
        out = self.fc2(x)

        return out

BatchNorm

class BN(nn.Module):
    def __init__(self, num_features, eps=1e-6, momentum=0.1):
        super(BN, self).__init__()
        self.fc1 = nn.Linear(1, num_features)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(num_features,1)

        # Scale,Shift params
        self.gamma = nn.Parameter(torch.ones(num_features))
        self.beta = nn.Parameter(torch.zeros(num_features))

        # Moving ave
        self.running_mean = torch.zeros(num_features)
        self.running_var = torch.ones(num_features)

        self.eps = eps
        self.momentum = momentum

    def forward(self, x):
        x = self.fc1(x)

        # Training or Evaluation?
        if self.training:
            mean = x.mean(dim=0)
            var = x.var(dim=0, unbiased=False)

            self.running_mean = (1-self.momentum) * self.running_mean + self.momentum * mean
            self.running_var = (1-self.momentum) * self.running_var + self.momentum * var

            # Normalize
            normalized_x = (x - mean) / torch.sqrt(var + self.eps)

        else:
            # Normalize during evaluation
            normalized_x = (x-self.running_mean) / torch.sqrt(self.running_var + self.eps)

        x = self.gamma * normalized_x + self.beta
        x = self.relu(x)
        out= self.fc2(x)
        return out

Train

def train(model, name, epochs=100, lr=0.05):
    optimizer = optim.SGD(model.parameters(),lr=lr)
    loss_fn = nn.MSELoss()
    losses = []
    with torch.no_grad():
        print(f"초기 출력 ({name}):", model(x[:5]).squeeze().numpy())

    for epoch in range(epochs):
        model.train()
        pred = model(x)
        loss = loss_fn(pred,y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        losses.append(loss.item())
    return losses

Training and Comparison

L2_model = L2()
BN_model = BN(num_features=10)

loss_L2 = train(L2_model, "L2 Normalization")
loss_BN = train(BN_model, "Batch Normalization")

Result

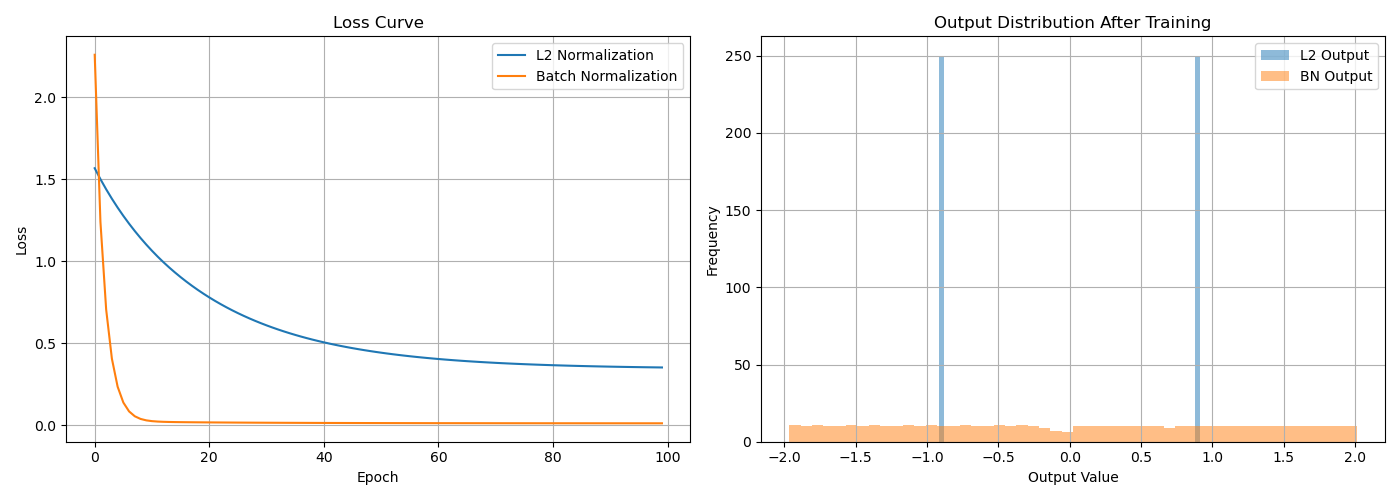
위 그래프를 보았을 때 L2 Normalization은 평균만 제거하여 분산이 그대로 유지되고 있어 출력값들이 좁은 범위에 몰려있다. 따라서 정규화되지 않은 Gradient가 흐른다고 볼 수 있으며 논문에서 제기된 문제인 Internal Covariant Shift 또한 그대로 남아있다.

반면에 Batch Normalization은 평균의 제거와 더불어 분산의 정규화까지 포함하여 zero-mean, unit-variance에 가깝다. 따라서 출력값의 분포가 표준 정규분포와 유사하게 퍼지고 Gradient도 안정적이라고 볼 수 있다.

Learning Rate Scaling

Learnning Rate를 각각 5배와 20배로 조정하여 Batch Normalization의 학습 안정성을 비교분석 하면 다음과 같은 결과를 가진다.

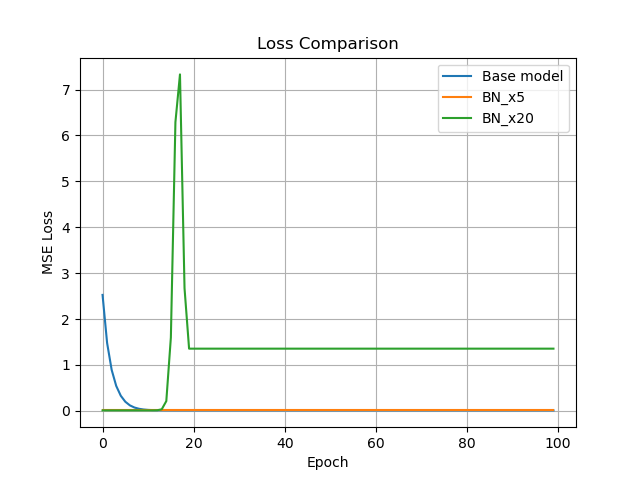
위 그래프를 분석해보면, LR을 5배 증가시킨 BN_x5모델은 Loss가 빠르게 0으로 수렴한 후 안정적으로 유지되었다. 이는 Batch Normalization이 gradient 흐름을 효과적으로 안정화시켜, 더 높은 학습률에서도 빠른 수렴이 가능함을 보여준다.

다만, 학습률을 20배 증가시킨 BN_x20모델은 초반 10 에폭까지는 BN_x5와 유사하게 수렴하였으나, 15-20 에폭 부근에서 gradient spike가 발생하였다. 그로인해 손실히 급등한 뒤 일정 수준에서 고정되는 모양새를 보이는데 이는 다음 두 가능성을 시사한다.

Gradient spike로 인한 일부 파라미터의 비정상적 갱신 및 고정
학습 중 moving average의 급격한 왜곡으로 인한 정규화 실패

이러한 현상은 Batch Normalization이 학습 안정화에 큰 도움이 되지만, LR이 지나치게 클 경우에는 모멘텀의 갱신이 왜곡되어 오히려 학습을 방해할 수 있음을 의미한다.

Parameter and Location of BN

두 가지 실험을 동시에 진행하였다.

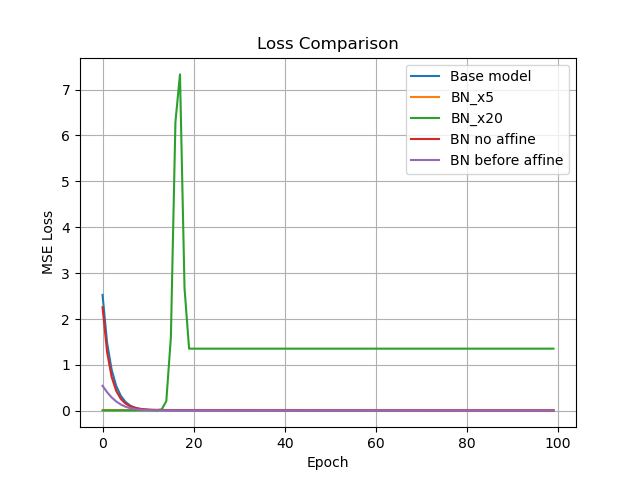
첫 번째로 ($\gamma,\beta$)없이 Batch Normalization을 구성하면 어떤 영향을 미치는지에 대해 실험을 진행하였다. 결론적으로 모멘텀 없이도 모델은 안정적으로 수렴하지만, 수렴 속도는 베이스 모델에 비해 약간 느리고 로스 최저점도 약간 높게 나타났다. 이는 scale, shift 없이도 Batch Normalization은 Internal Covariate Shift를 줄이고 학습을 돕지만, 표현력이 다소 줄어들어 성능 저하의 가능성을 유발한다. 또한 활성값의 scale, shift 조정이 불가능하므로 ReLU 이후 표현의 유연성이 줄어든다.

두 번째로 모멘텀 전달 이전에 Batch Normalization을 적용했을 때 어떤 영향을 미치는지에 대해 실험을 진행하였다. 일반적인 순서(FC -> BN -> ReLU)를 변형(BN -> FC -> ReLU)하여 적용하였음에도 불구하고 성능이 좋다는 점에서 학습 초기 정규화의 위치가 학습 효과에 큰 영향을 줄 수 있음을 시사한다. 구체적으로 모든 모델 중에 가장 빠르고 매끄럽게 수렴했으며, BN이 입력 분포를 안정화시켜 파라미터 업데이트에 유리하게 작용한 것으로 해석된다.

Conclusion

Batch Normalization은 단순한 정규화 기법이 아닌 딥러닝의 학습 안정성과 효율성에 근본적인 영향을 주는 핵심 구성 요소로 자리잡았다. 위 실험을 통해 논문의 구현을 넘어, 다양한 하이퍼 파라미터와 구조 실험을 통해 Batch Normalization의 작동 원리와 설계 시의 고려사항을 탐색해보았다는 점에 의의를 둔다.

IMPLEMENTATION - Batch Normalization